одним из основных понятий математики и поэтому не определяется
через другие.Множества принято обозначать прописными буквами латинского алфавита: A, B, C, …, Z.
Множество, не содержащее ни одного объекта, называется пустым и обозначается так: Ø
Объекты, из которых образованно множество, называются элементами.
Элементы множества принято обозначать строчными буквами латинского алфавита: a, b, c, …, z.
Множества бывают конечными (множество дней в неделе, месяцев в году) и бесконечными (множество натуральных чисел, точек на прямой)














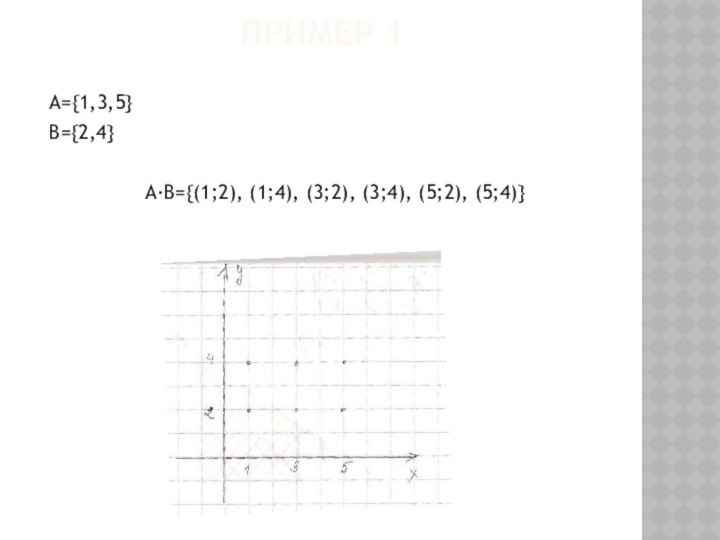
![Презентация по теме: Множества и операции над ними Пример 2А={1,3,5}В=[2,4] или В={у|у Є R, 2≤у≤4}](/img/tmb/7/606412/f51dd9a06dde9196a632a0f0fa548dc5-720x.jpg)
![Презентация по теме: Множества и операции над ними Пример 3А=[1;5]В={2,4}](/img/tmb/7/606412/b02e1e9a683ba7066c7e82e0019fb979-720x.jpg)
![Презентация по теме: Множества и операции над ними Пример 4А=[1;5]В=[2,4]](/img/tmb/7/606412/4d6fb0816e09b2dbcf457f33dc385736-720x.jpg)
![Презентация по теме: Множества и операции над ними Пример 5А=[1;5)В=(2,4]](/img/tmb/7/606412/50a9232064965925861865f5a35669cf-720x.jpg)