Слайд 2
Базовые понятия теории вероятностеи
Опыт
Событие
Переменная величина
Слайд 3
Понятие опыт
Определение. Под опытом понимается воспроизведение некоторого комплекса
условий. При этом предполагается, что опыт может быть повторен
сколько угодно раз
Пример 1. Экономический объект – рынок подержанных автомобилей
Опыт – продажа конкретного автомобиля
Комплекс условий: наличие автомобилей, покупателей и сделок купли продажи
Данные условия можно повторить много раз
Пример 2. Бросание игрального кубика
Опыт- бросок
Комплекс условий- наличие кубика и игроков
Пример 3. Объект- элементарная макромодель Кейнса:
С=a0 + a1Y + U
Y= C + I
Опыт- функционирование экономики
Комплекс условий- наличие инвесторов и потребителей
Слайд 4
Понятие события
Определение. Пусть имеется некоторый опыт Событие, связанное
с этим опытом, называется любой его исход.
При этом событие
называется случайным, если оно может появиться или не появиться в данном опыте
Обозначение: D: (описание события)
Пример 1. Опыт-продажа подержанных автомобилей
Случайное событие- продажа 3-х летнего автомобиля за 0.5 цены.
Это событие может появиться, а может и не появиться при повторении опыта.
Пример 2. Опыт-бросание игрального кубика
События: A: (Выпадение четного числа)
B: (Выпадение шестерки)
Слайд 5
Вероятность появления события
Мерилом возможности появления события A: в
данном опыте служит вероятность появления этого события в опыте
Определение.
Пусть А- случайное событие, связанное с некоторым опытом Предположим, что опыт повторен n раз, в итоге событие А появилось в опытах na раз Тогда дробь na/n называется относительной частотой появления события А в опытах, а вероятность P(A) появления события А определяется как предел этой дроби при многократном повторении опыта:
(3.1)
Слайд 6
Свойства вероятности события
1. Вероятность события приближенно равна относительной
частоте появления события: P(A) ≈ nA/n
2. Из определения следует,
что область определения P(A) – интервал (0, 1)
Замечание. Иногда вероятность случайного события можно определить априори не прибегая к испытаниям
Например, опыт с игральным кубиком, вероятность появления любого числа из набора (1 2 3 4 5 6) одинакова и равна 1/6.
Слайд 7
Достоверное и невозможное события
Определение. Пусть R событие, связанное
с некоторым опытом, которое всегда появляется при его повторении,
т.е P(R)≡1. Тогда событие R называется достоверным событием
Определение. Пусть I событие, связанное с некоторым опытом, которое никогда не появляется при его повторении, т.е P(I)≡0. Тогда событие I называется невозможным событием
Пример.
Опыт - бросание игральной кости:
выпадение любого числа из набора (1 2 3 4 5 6) – событие достоверное
выпадение числа 7 – событие невозможное
Слайд 8
Практически достоверное событие
Определение. Событие V, связанное с некоторым
опытом, называется «практически достоверным», если вероятность его появления удовлетворяет
условию: 0.95≤P(V)≤1
Любое случайное событие W, связанное с опытом, вероятность которого 0
Установлено, что практически достоверное событие, как правило, появляется при первом проведении опыта
Если этого не происходит, значит нарушены условия опыта
Слайд 9
Условная вероятность
Определение. Пусть А и В два события,
связанные с опытом, причем Р(А)>0. Проведено такое количество опытов
N, при котором Na>0 (количество появлений события А). Пусть Nab количество опытов, в которых событие В появилось вместе с событием А Отношение Nab/Na называют относительной частотой появления события В при условии появления события А
Условная вероятность появления события В есть:
Свойства: P(A|B) ≈ Nab/Na 0 ≤ P(A|B) ≤ 1
(3.2)
Слайд 10
Вероятность совместного события
Разделив числитель и знаменатель (3.2) на
N, получим:
(3.3)
где P(AB) – вероятность появления одновременно событий
А и В в N опытах
Пример с кубиком. А:(четное число), В:(число 6)
P(A)=1/2, P(B)=1/6. Тогда P(B|A)=(1/6)/(1/2)=1/3
Событие В совпадает с событием АB, след. P(AB)=P(B)=1/6. Отметим, Р(В)≠Р(В|А)
Р(В) = Р(В|А) – условие независимости событий
Слайд 11
Теорема умножения вероятностей
Теорема. Если события А1, А2,…, Аn
суть независимые события, то для них справедливо равенство:
Р(А1,
А2,…, Аn)=Р(А1)Р(А2)…Р(Аn)
где: Р(А1)Р(А2)…Р(Аn) – вероятности появления каждого события
Пример. Бросание двух кубиков.
Событие А:(появление 6 на кубе 1)
Событие В:(появление 6 на кубе 2)
Р(А)=1/6, Р(В)=1/6
Вероятность появление двух чисел 6 одновременно:
Р(АВ)=Р(А)Р(В)=(1/6)(1/6)=1/36
Слайд 12
Понятие переменная
Определение. Пусть задано множество значений Ах{t1,t2,…tn}. Тогда
величина Х называется переменной, если она может принимать любые
значения из множества Ах, а множество Ах называется областью допустимых значений или областью определения Х
Если Ах состоит из набора значений, которые можно пронумеровать (счетное множество), то Х – дискретная переменная
Если Ах представляет собой отрезок или интервал на числовой оси, то такая переменная называется непрерывной
Слайд 13
Дискретная случайная переменная
Определение. Дискретная переменная Х с множеством
допустимых значений Ах называется случайной, если все ее возможные
значения появляются в некотором опыте со случайными исходами А:(x=t) и если для нее задан закон распределения вероятностей
Первое свойство объединяет все случайные переменные
Второе свойство – обеспечивает индивидуальность каждой случайной переменной
Слайд 14
Закон распределения дискретной случайной переменной
Определение. Законом распределения дискретной
случайной величины Х называется функция Px(t), определенная на всей
числовой оси, значения которой характеризуют вероятность появления в данном опыте события В:(x=t), и определяется по правилу:
где: Р(х=t) вероятность события В:(x=t)
Закон распределения ДСП называют вероятностной функцией
Слайд 15
Классические примеры дискретных случайных переменных
Пример 1. Бросание кубика
Ax={1,2,3,4,5,6}
– область определения
X- цифра на верхней грани (СДП)
Закон распределения
–
Пример равновероятного закона распределения
Графическое представление равновероятного закона распределения
Слайд 16
Классические примеры дискретных случайных переменных
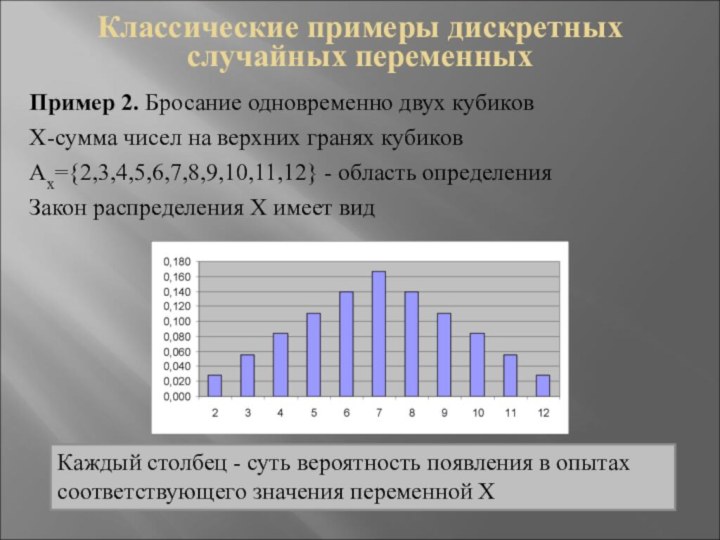
Пример 2. Бросание одновременно
двух кубиков
X-сумма чисел на верхних гранях кубиков
Ax={2,3,4,5,6,7,8,9,10,11,12} - область
определения
Закон распределения Х имеет вид
Каждый столбец - суть вероятность появления в опытах соответствующего значения переменной Х
Слайд 17
Закон распределения непрерывной случайной переменной
В случае, когда Х
непрерывная случайная переменная, ее закон распределения вероятностей выражается с
помощью функции плотности вероятностей, который по определению есть:
где: P(t≤x≤t+Δt) – вероятность того, что случайная переменная Х примет в опыте значение, лежащее в интервале (t, t+Δt)
Слайд 18
Свойства функции плотности вероятностей
1. Функция плотности вероятности неотрицательна
px(t)≥0
2. Вероятность попадания СВ х на отрезок [a, b]
есть:
3. Функция распределения вероятностей связана с функцией плотности вероятностей выражением:
4. Справедливо равенство:
Слайд 19
Примеры законов распределения непрерывных случайных переменных
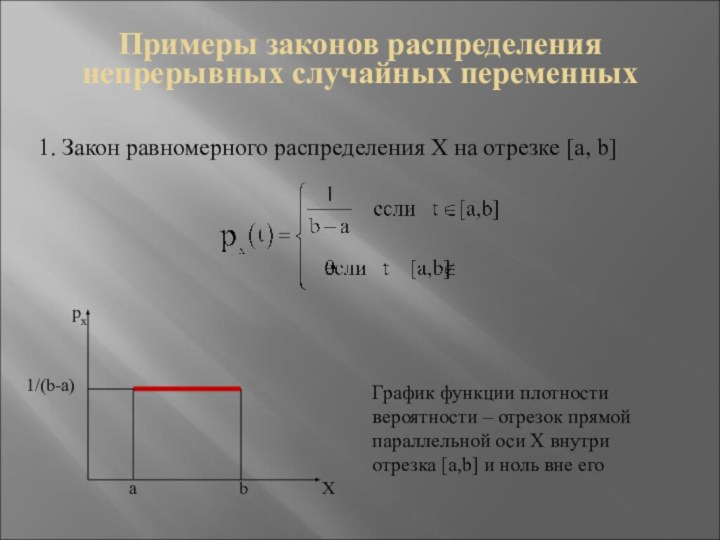
1. Закон равномерного
распределения Х на отрезке [a, b]
a
b
1/(b-a)
px
График функции плотности вероятности
– отрезок прямой параллельной оси Х внутри отрезка [a,b] и ноль вне его
Х
Слайд 20
Примеры законов распределения непрерывных случайных переменных
2. Нормальный закон
распределения Гаусса
где a и s –параметры закона распределения.
Именно,
с помощью значений этих параметров удается персонифицировать различные случайные переменные, подчиняющиеся нормальному закону распределения