Презентация на тему по алгебре История развития понятия функция

подумаешь о том,
Как важно будет в жизни это слово
И

сколько смысла будет в слове том!
Его по-разному с годами толковали.
Сам Лобачевский руку приложил,
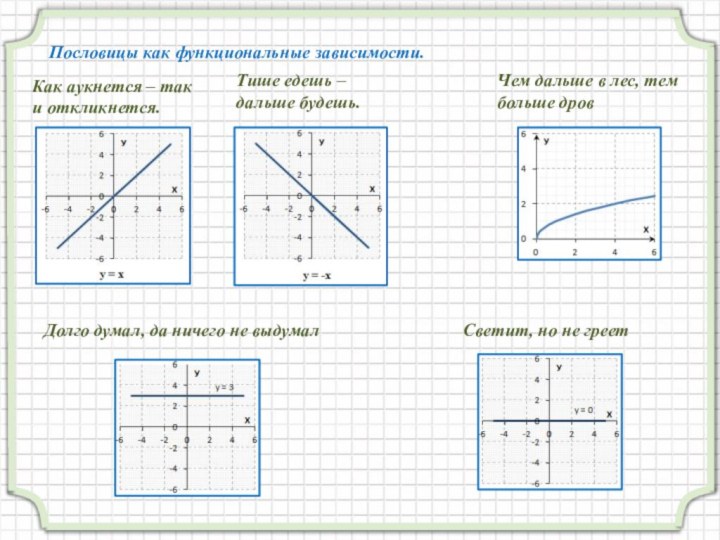
Чтоб слово «функция» и в средней школе знали,
Чтоб каждый ученик им дорожил!
Без функции не сдашь простой экзамен,
Без функции ты не войдешь в предмет!
Без функции не разгорится пламя!
Без функций никакой науки нет!

и изучили линейную функцию. Но у меня осталось много

вопросов:
в первую очередь, как долго человечество шло к осознанию того, что связи между объектами природы и мира можно определить одним понятием функция;
на сколько широко используется в природе и науке простая линейная функция.
В ходе подготовки данной работы, я полностью удовлетворила своё любопытство. Теперь я хочу рассказать об этом Вам.
Надеюсь, что будет интересно!

17 века.
Египетские цари, разделив землю между египтянами, брали с

каждого из них ежегодный налог, пропорциональный площади занимаемого участка.

Вавилонские ученые (4 – 5 тыс. лет назад) установили, что площадь круга является функцией от его радиуса: S=3r2

Вавилоняне, индийцы, древние греки пользовались астрономическими таблицами. ( Табличное задания функции. )

Теорема о постоянстве отношения площадей круга и квадрата на его диаметре - словесное задание функции.

века).
Франсуа Виет (1540 – 1603гг.)
Рене Декарт
(1596-1650гг.)


Готфрид Вильгельм

фон Лейбниц
(1646 – 1716).

Иоганн Бернулли

Леонард Эйлер
(1707 – 1783).

Дали общее понятие функции и разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание.

Впервые употребил само слово «функция» (от латинского functio — совершение, выполнение) в 1673 г. Впервые ввёл термины «константа» и «переменная».

В 1718 году опре-делил функцию .

В 1748 г. Ввел окончатель-ную формули-ровку опреде-ления функции с аналитичес-кой точки зре-ния .

это изменение ординаты точки в зависимости от изменения ее

абсциссы “

Иоганн Бернулли ( 1718 г.)
“…функцией переменной величины называют количество, образованное каким угодно способ из этой переменной величины и постоянных”

Леонард Эйлер ( 1755 г. )
"Когда некоторые количества зависят друг от друга таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функцией вторых".

Л. Дирихле
( 1805-1859 гг. )

называть число, которое дается для каждого X и вместе

с X постепенно изменяется. Значение функции может быть дано или аналитическим выражением или условием, которое подает средство испытать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной».

П. Л. Дирихле ( 1837 г. )
«…Y есть функция переменной X (на отрезке a < X < b), если каждому значению X на этом отрезке соответствует совершенно определенное значение Y, причем безразлично, каким образом установлено это соответствие - аналитической формулой, графиком, таблицей либо даже просто словами».

не изучали. Но мы уже знаем, что такое степень,

а значит вид уравнений кубической и квадратичной функций нам знаком. Точно также нам уже известно понятие обратной пропорциональности. Её выражение мы много раз применяли в решении задач.
Красным цветом отмечена функция, которую мы изучаем в 7 классе.
Все функции, представленные на схеме, являются аналитическими, задаются формулой и могут быть представлены в виде графика.

X, если каждому значению X соответствует единственное значение Y.

Переменная X - независимая переменная или аргумент.
Переменная Y - зависимая переменная.
Значение функции - значение Y, соответствующее заданному значению X.
Область определения функции- все значения, которые принимает независимая переменная.
Область значений функции (множество значений)- все значения, которые принимает функция.

числу ставится в соответствие его модуль >.

человеческому познанию одинаково вытекает одно из другого".
А российский математик,

замечательный ученый, педагог, поэт А.Я. Хинчин считал, что «…ни одно из других понятий не отражает явлений реальной действительности с такой непосредственностью и с такой конкретностью, как понятие функциональной зависимости, в которой воплощены и подвижность, и динамичность реального мира, и взаимная обусловленность реальных величин».

пройду равномерно любую дистанцию.
Нелинейность во мне вызывает презрение,
И

всегда постоянно мое ускорение.
Чту законы, с которыми лично знакома.
Например, знаменитое правило Ома
Для цепей, по которым бежит электричество.
И в торговле я смыслю: чем больше количество
Покупаемых тряпок, колбас или фенек
Тем в мошне твоей меньше останется денег!
Для всего, что хоть как-то линейно зависимо
Тут же выстрою график и браво! Брависсимо!
Замечательна роль – для любого клиента-
Моего углового коэффициента.
Если он положителен, то я возрастаю,
Отрицательный – я постепенно растаю.
Его модуль приводит меня в обалденье:
Чем он больше, тем круче мое поведение!

Свойства линейной функции.

+ b, заданная на множестве всех действительных чисел. Здесь

k – угловой коэффициент (действительное число),
b – свободный член (действительное число),
X – независимая переменная.

В уравнении функции Y=kX+b коэффициент k отвечает за наклон графика функции:

если k>0, то график наклонен вправо,
если k<0 , то график наклонен влево.
Коэффициент b отвечает за сдвиг графика вдоль оси OX.

коэффициентов k и b.

( 0,b )
OX – ( -b/k )

Y=kX, при k≠0.
Зависимость между переменными X и Y

является прямопропорциональной. График проходит через начало координат.
Если k=-1, то Y=-X, т.е. прямая является биссектрисой 2 и 4 координатных углов.
Если k=1, то Y=X , то прямая является биссектрисой 1 и 3 координатных углов.

Есть ещё один совершенно особый вид графика: X=a при Y=0. Этот график представляет собой прямую линию, параллельную оси OY, все точки которой имеют абсциссу X=a.
Уравнение x=a не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

значение из множества действительных чисел ( - ∞; +

∞).
Зависимая переменная Y принимает значения из множества действительных чисел ( - ∞; + ∞).
Точки пересечения графика с осями координат:
- с осью OY – X=0, Y=b
- с осью OX – Y=0, X=-b/k

Промежутки знакопостоянства:

eсли k>0, то Y>0 при X> -b/k, Y<0 при X< -b/k,

если k<0, то Y>0 при X< -b/k, Y<0 при X> -b/k.

возрастает на всей числовой оси,
если k

убывает на всей числовой оси.

Наибольших и наименьших значений функции не существует, так как графиком является прямая, а прямая бесконечна.

движения есть прямая линия и точка за любые равные

промежутки времени проходит равные расстояния.
S = V * t
S – путь, V – скорость, t – время.
Плот двигается по течению реки. Скорость течения 4 м/с.

Тела, окружающие нас, состоят из различных веществ: дерева, железа, резины, пластика и т.д. Разные вещества имеют разную плотность.
m = ƥ * V
m – масса, ƥ – плотность, V – объём.
ƥ – величина постоянная для каждого вещества. Поэтому масса тела пропорциональна его объёму.
График зависимости массы деревянного пола от его объёма.

Зависимость массы тела от объёма

находящееся в жидкости, действует сила, выталкивающая это тело из

жидкости. Силу, выталкивающую тело из жидкости или газа, называют архимедовой силой.
Fa = g * m
F – сила, ġ – ускорение свободного падения, m – масса жидкости.
Архимедова ( или выталкивающая ) сила прямо пропорциональна весу жидкости, вытесненной телом.

Математика

Зависимость длины окружности от длины её радиуса

Опытным путём было установлено, что длина окружности зависит от её радиуса. Эта зависимость выражается формулой C=2πR и является прямой пропорциональной зависимостью с угловым коэффициентом равным 2 π.
С – длина окружности, R – радиус.

смежных углов выражается формулой:
У2 = -1∗У1+180
У1 – первый

из смежных углов, У2 – второй из смежных углов.

География.

Построение географических карт.

В верхнем правом углу карты указан
масштаб 1:10000. Это означает, что расстояние
на местности в 10000 раз больше чем расстояние
на карте.
Отсюда получаем линейную зависимость:
У=10000*Х

можно измерять в градусах Цельсия и по Фаренгейту. Между

этими шкалами существует линейная зависимость. Для того, чтобы её установить составим табличку:

Когда температура по Цельсию возрастает на 1, температура по Фаренгейту вырастет на (212-32)/100=1.8. Значит F=32+1.8T. Если выразить отсюда Т, то получим: Т=5/9(F-32).

Психология, медицина.

Количество часов сна в зависимости от возраста ребёнка.

Медиками установлено, что для нормального развития ребёнок или подросток, которому Т лет ( T<18 ), должен спать в сутки t часов,

выполнения работ
Затраты на перевозку одного и того же груза

двумя разными видами транспорта определяются формулами:

У1 = 1000 + 4х,
У2 = 2000 + 2х,
Где х – расстояние в километрах,
У1 ,У2 – стоимость перевозки в рублях.
При 0 < Х < 500 км, выгоднее пользоваться первым видом транспорта.
Начиная с расстояния в 500 км. экономичнее становится второй вид транспорта.

хотят и могут приобрести покупатели за определенный период времени

при всех возможных ценах на этот товар.
Предложение — это количество товара, которое хотят и могут предложить на рынок продавцы за определенный промежуток времени при всех возможных ценах на этот товар.
функция спроса задана формулой Q1=7-P, а функция предложения – Q2=2*P+5.
Q1- объём спроса в млн. штук в год,
Q2 – объём предложения в млн. штук в год,
P – цена в тыс. рублей.

равновесия, а цена P, соответствующая этой точке – равновесной

ценой. При этой цене желание и готовность покупателей приобрести товар, а также желание и готовность продавцов его продать совпадают – не будет ни излишков, ни дефицита.
Если продавец захочет продать товар по цене P2, то покупатель будет готов купить в количестве Q1, а продавец захочет предложить в количестве Q2. Тогда Q2-Q1 – избыток товара.
Если цена у продавца будет P1, то он сможет предложить товар в количестве Q1, а покупатель захочет купить его в количестве Q3. Тогда Q3-Q1 – дефицит товара.
Поэтому очень важно найти равновесную цену.

откликнется.
Тише едешь – дальше будешь.
Чем дальше в лес, тем

больше дров

Долго думал, да ничего не выдумал

Светит, но не греет

различных функций надо воспользоваться кусочно-заданной функцией.
Кусочно-заданная функция – это

функция, заданная на каждом из интервалов, составляющих область определения, отдельной формулой.

любому делу относиться творчески, с интересом, то даже такая

сложная наука, как математика становиться более понятной, доступной и интересной, что очень важно.
Не прав тот, кто считает математику скучной и сухой наукой. Еще С. Пуассон сказал: «Жизнь украшается двумя вещами: знанием математики и ее преподаванием».
Карьерный рост, линия жизни, биоритмы, статистические данные, прогресс, регресс и другие отношения мы можем представить в виде линейной или кусочно-линейной функции.
Выводы:
Величины разной природы могут быть связаны между собой зависимостью одного и того же вида.
Математика дает универсальные инструменты для изучения связей, зависимостей между различными величинами. Её изучение делает шире и богаче наши возможности математического описания окружающего мира.
Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира. Функция является неотъемлемой частью нашей жизни и науки в целом.