Презентация на тему Детская работа по математике на тему Теорема Безу Наталья Криводуд

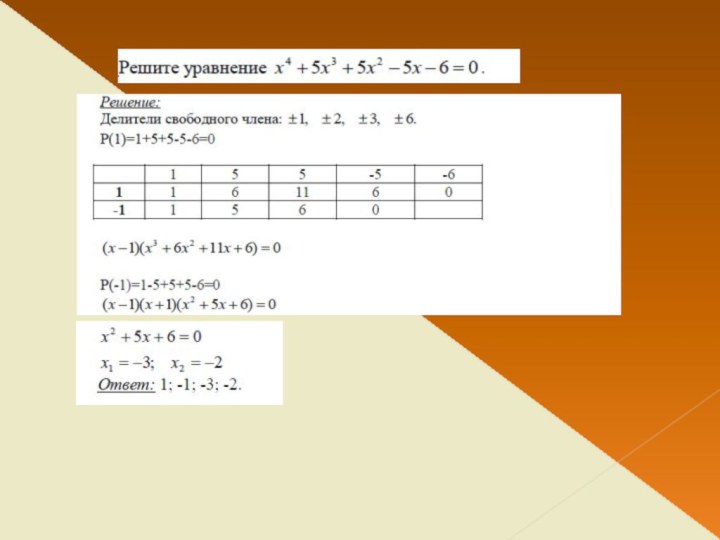
член Парижской академии наук

Преподавал математику в Училище гардемаринов

(1763) и Королевском артиллерийском корпусе (1768).

Основные его работы относятся к алгебре (исследование систем алгебраических уравнений высших степеней, исключение неизвестных в таких системах и др.)
Автор шеститомного«Курса математики» (1764-1769),неоднократно переиздававшегося.

двучлен (х – а) равен Р(а)

Доказательство.
Поделим с остатком многочлен

Р(х) на двучлен (х – а):
Р(х) = Q(х) (х – а) + R(х)
Т.к. степень R меньше степени (х – а), то R(х) – многочлен нулевой степени, т.е.
R(х) = R – число.

При х = а, имеем Р(а) = Q(а) (а – а) + R(а.
Р(а) = R(а). чтд

двучлен (х – а) равен Р(а)

Следствия
Число a является корнем

многочлена Р(х) тогда и только тогда, когда Р(х) делится без остатка на двучлен (х – а)
(отсюда, в частности, следует, что множество корней многочлена тождественно множеству корней соответствующего уравнения)

Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами
(если старший коэффициент равен 1, то все рациональные корни являются и целыми)

Пусть α — целый корень приведённого многочлена A(x) с целыми коэффициентами. Тогда для любого целого k число A(k) делится на α-k

Если число а является корнем многочлена Р(х), то этот многочлен можно представить в виде произведения (х – а) Р1(х), где Р1(х) - многочлен n-1–й степени.

Приложения
Теорема Безу и следствия из неё позволяют легко находить рациональные корни уравнений с целыми (рациональными) коэффициентами.

по теории алгебраических уравнений.
С его именем связана (1819)

схема Горнера деления многочлена на двучлен .

схемы Горнера)