Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему к теме Комплексные числа 11класс

Содержание

Не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве. Если хотите, комплексное число – это двумерное число.
Учитель математики высшей категории Селезнева Ольга Евлампиевна гимназия №1 г.БелебеяКомплексные числа в 11 классе Не пытайтесь представить комплексное число «в жизни» – это всё Натуральные числа (N)1, 2, 3, 4, 5, 6, 100, 256… Отрицательные числа-1; -2; -796; -4,5; -9; … Целые числа (Z)1, 2, 5, 937, 577, 0, -2, -67,… (мнимая единица) Алгебраическая форма комплексного числа z=a+bi, а –действительная часть числа, Тригонометрическая форма комплексного числа Показательная форма комплексного числа. Любое комплексное число (кроме нуля)   Комплексным числом z называется число вида z=a+bi, где a и b – действительные числа, i – Сложим два комплексных числа Найдём разность комплексных чисел , =-i Найдём произведение комплексных чисел: ( - 2 + i ) ( Найдём частное комплексных чиселумножим на сопряженное ( 7 + 6i) Решим квадратное уравнениеРешить квадратное уравнение Вычислим дискриминант: Дискриминант отрицателен, и в действительных «Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из мира Спасибо за внимание!
Слайды презентации

Слайд 2 Не пытайтесь представить комплексное число «в

Не пытайтесь представить комплексное число «в жизни» – это всё

жизни» – это всё равно, что пытаться представить четвертое

измерение в нашем трехмерном пространстве. Если хотите, комплексное число – это двумерное число.

Слайд 3 Натуральные числа (N)
1, 2, 3, 4, 5, 6,

Натуральные числа (N)1, 2, 3, 4, 5, 6, 100, 256…

100, 256…

Слайд 4 Отрицательные числа
-1; -2; -796; -4,5; -9; …

Отрицательные числа-1; -2; -796; -4,5; -9; …

Слайд 5 Целые числа (Z)
1, 2, 5, 937, 577, 0,

Целые числа (Z)1, 2, 5, 937, 577, 0, -2, -67,…

-2, -67,…

Слайд 6

Слайд 7

(мнимая единица)

(мнимая единица)

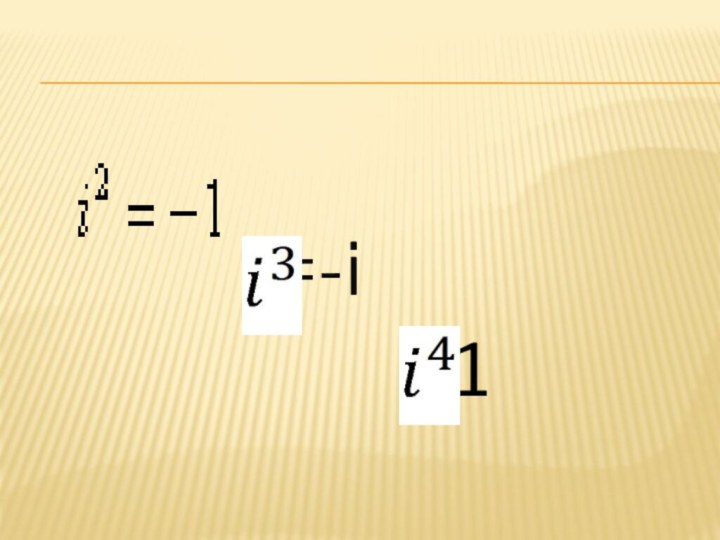
Слайд 8 Алгебраическая форма комплексного числа
z=a+bi, а

Алгебраическая форма комплексного числа z=a+bi, а –действительная часть числа, b – мнимая часть комплексного числа.

–действительная часть числа, b – мнимая часть комплексного числа.

Слайд 9 Тригонометрическая форма комплексного числа

Тригонометрическая форма комплексного числа


, где   – это модуль комплексного числа, а   – аргумент комплексного числа.

Слайд 10 Показательная форма комплексного числа.
Любое комплексное число (кроме

Показательная форма комплексного числа. Любое комплексное число (кроме нуля)  

нуля)  

можно записать в показательной форме: , где   – это модуль комплексного числа, а  – аргумент комплексного числа.

Слайд 11 Комплексным числом z называется число вида z=a+bi, где a и

Комплексным числом z называется число вида z=a+bi, где a и b – действительные числа,

b – действительные числа, i – так называемая мнимая единица. Число

a называется действительной частью (Re z ) комплексного числа , число b называется мнимой частью (Im z ) комплексного числа z.

Определение

Слайд 12 Сложим два комплексных числа

Сложим два комплексных числа ,


,

Слайд 13 Найдём разность комплексных чисел

Найдём разность комплексных чисел , если ,

, если

,

Слайд 14

=-i =1

=-i

=1

Слайд 15 Найдём произведение комплексных чисел:
( - 2 +

Найдём произведение комплексных чисел: ( - 2 + i ) (

i ) ( 3 + 5i) = - 6

– 10i +3i +5 =
= -6 – 7i – 5 = - 11 – 7i.

Слайд 16 Найдём частное комплексных чисел

умножим на сопряженное ( 7

Найдём частное комплексных чиселумножим на сопряженное ( 7 + 6i)

+ 6i)

Слайд 17 Решим квадратное уравнение
Решить квадратное уравнение
Вычислим дискриминант:
Дискриминант отрицателен,

Решим квадратное уравнениеРешить квадратное уравнение Вычислим дискриминант: Дискриминант отрицателен, и в

и в действительных числах уравнение решения не имеет. Но

корень можно извлечь в комплексных числах!
По известным формулам получаем два корня:   – сопряженные комплексные корни

Слайд 18 «Дух божий нашёл тончайшую отдушину в этом чуде

«Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из

анализа, уроде из мира идей, двойственной сущности, находящейся между

бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы». Писал Лейбниц
  • Имя файла: prezentatsiya-k-teme-kompleksnye-chisla-11klass.pptx
  • Количество просмотров: 211
  • Количество скачиваний: 3
- Предыдущая Фрагмент урока - Обучение лексической стороне иноязычной речи What is the weather like?
Следующая - Мониторинг социально-экономического состояния и физического развития учащихся

Похожие презентации

Презентация по алгебре Обозначения.Знаки и символы в математике Презентация по алгебре Обозначения.Знаки и символы в математике 226
Презентация по алгебре в 11 классе по теме Производная и ее геометрический смысл. Презентация по алгебре в 11 классе по теме Производная и ее геометрический смысл. 152
Презентация по алгебре на тему Умножение многочлена на одночлен (7 класс) Презентация по алгебре на тему Умножение многочлена на одночлен (7 класс) 178
Презентация по алгебре по теме Функция (7 класс) Презентация по алгебре по теме Функция (7 класс) 166
Презентация по математике Как построить график функции у=f(x) + m Презентация по математике Как построить график функции у=f(x) + m 172
Вписанные, центральные углы Вписанные, центральные углы 217
Произведение разности и суммы двух выражений Произведение разности и суммы двух выражений 194
Презентация по теме Методы решения систем линейных уравнений Презентация по теме Методы решения систем линейных уравнений 155
Понятие цилиндра Понятие цилиндра 166
Классификация функций Классификация функций 156
Презентация по алгебре на тему: Теорема Виета (8 класс) Презентация по алгебре на тему: Теорема Виета (8 класс) 170
Что такое Функция? Что такое Функция? 156
Урок-деловая игра по математике в 9 классе по теме: Решение заданий ОГЭ. Презентация Урок-деловая игра по математике в 9 классе по теме: Решение заданий ОГЭ. Презентация 301
Урок–игра В царстве квадратных корней Урок–игра В царстве квадратных корней 139
Числовые и буквенные выражения (7 класс) Числовые и буквенные выражения (7 класс) 197
Определенный интеграл Определенный интеграл 150
Такое далёкое и близкое прошлое Такое далёкое и близкое прошлое 172
Доказательства теоремы Пифагора Доказательства теоремы Пифагора 171
Противоположные числа Противоположные числа 148
Свойства логарифмической функции Свойства логарифмической функции 148
Презентация к уроку-проекту Положительные и отрицательные числа Презентация к уроку-проекту Положительные и отрицательные числа 191
Показательная функция. Показательные уравнения Показательная функция. Показательные уравнения 180
Презентация по математике на тему Умножение одночлена на многочлен(7 класс) Презентация по математике на тему Умножение одночлена на многочлен(7 класс) 142
Решу ВПР: запись чисел с использованием разных систем измерения. Часть 4 Решу ВПР: запись чисел с использованием разных систем измерения. Часть 4 235
Презентация к уроку алгебры на тему: Графический способ решения систем уравнений (9 класс) Презентация к уроку алгебры на тему: Графический способ решения систем уравнений (9 класс) 148
Презентация по математике на тему Построение графиков функций при помощи геометрических преобразований Презентация по математике на тему Построение графиков функций при помощи геометрических преобразований 233
Урок Решение квадратных уравнений Урок Решение квадратных уравнений 136
Квадратные уравнения Квадратные уравнения 141
Презентация к бинарному уроку(математика и биология) в 7 классе Презентация к бинарному уроку(математика и биология) в 7 классе 182
Презентация к уроку в 7 классе ВОЗВЕДЕНИЕ ПРОИЗВЕДЕНИЯ И СТЕПЕНИ В СТЕПЕНЬ Презентация к уроку в 7 классе ВОЗВЕДЕНИЕ ПРОИЗВЕДЕНИЯ И СТЕПЕНИ В СТЕПЕНЬ 170