Успешного
усвоения нового материала
Знание –
самое превосходное из владений.
Все стремятся к нему,
само же оно не приходит.
Ал - Бируни
Слайд 3
Стр.26,№ 33(3,4)
Проверка ДР № 5 на 17.09.18
3) 0,1с
– 0,3 +d – c – 2,1d =
=– 0,9c
– 1,1d– 0,3
Слайд 4
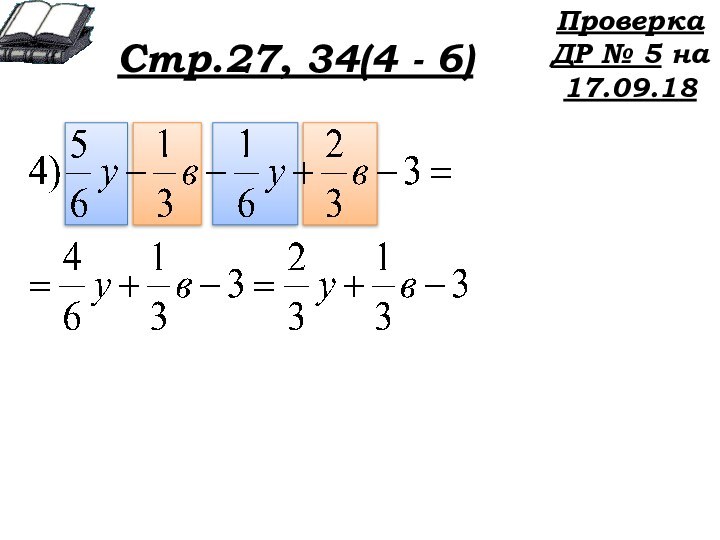
Стр.27, 34(4 - 6)
Проверка ДР № 5 на
17.09.18
Слайд 5
Стр.27, 34(5,6)
Проверка ДР № 5 на 17.09.18
5) 2,1т+п–3,2т+2п+1,1т–п=
=0·т + 2п=2п
6)5,7р–2,7q+0,3p+0,8q+1,9q– p
=5p
Слайд 6
Стр. 27, №,36(4)
Проверка ДР № 5 на 17.09.18
4)
0,01(2,2x – 0,1)+0,1(x –100)=
=0,01·2,2x –0,01·0,1 +
+0,1x –0,1·100 =
=0,022x
– 0,001+0,1x – 10= =0,122x – 10,001
0,122x – 10,001=…
Слайд 7
Стр. 27, №,36(4)
Проверка ДР № 5 на 17.09.18
4)
0,122x–10,001=
=0,122·(–10)–10,001=
=
–1,22–10,001= –11,221
Слайд 8
**Стр.27,
№38(1,3,4)
Проверка ДР № 5 на 17.09.18
1,2a –
(0,2a+b) =
=1,2a – 0,2a – b =
=a– b
Слайд 9
**Стр.27,
№38(1,3,4)
Проверка ДР № 5 на 17.09.18
3) 0,1(x
– 2y) + 0,2(x + y)=
=0,1x – 0,2y
+ 0,2x +0,2y
=0,3x
Слайд 10
**Стр.27,
№38(1,3,4)
Проверка ДР № 5 на 17.09.18
Слайд 11
Оцените ДР:
- все ответы верны и подробно
записано решение
«5»
- все ответы верны и подробно записано решение, но допущены вычислительные ошибки «4»
- ответы верны, но решение либо неполное, либо его нет совсем «3»
-домашняя работа отсутствует- «2»
17.09.2018
КР.
Правила раскрытия скобок. §5.
Слайд 13
Цели урока:
Закрепить свойства арифметических действий
Выполнять упрощение алгебраических выражений.
Продолжить формировать культуру устной и письменной математической речи.
Слайд 14
Устная работа
Выполните действия:
Слайд 15
Закрепление понятий
Назовите каждую из формул:
Слайд 16
Закрепление понятий
Назовите каждую из формул:
Формула
площади прямоугольника
Слайд 17
Закрепление понятий
Формула
площади прямоугольника
Формула
периметра прямоугольника
Назовите каждую из формул:
Слайд 18
Закрепление понятий
Формула
площади прямоугольника
Формула
периметра прямоугольника
Формула
пути
Назовите каждую из формул:
Слайд 19
Закрепление понятий
Формула
площади прямоугольника
Формула
периметра прямоугольника
Формула
пути
Формула
длины окружности
через радиус
Назовите каждую из формул:
Слайд 20
Закрепление понятий
Формула
площади прямоугольника
Формула
периметра прямоугольника
Формула
пути
Формула
длины окружности
через радиус
Формула
площади круга через радиус
Назовите каждую из
формул:
Слайд 21
Закрепление понятий
Формула
площади прямоугольника
Формула
периметра прямоугольника
Формула
пути
Формула
длины окружности
через радиус
Формула
площади круга через радиус
Формула
периметра треугольника
Назовите каждую
из формул:
Слайд 22
Закрепление понятий
Назовите каждую из формул:
Слайд 23
Закрепление понятий
Формула
площади квадрата
Назовите каждую
из формул:
Слайд 24
Закрепление понятий
Формула
площади квадрата
Формула
периметра квадрата
Назовите каждую из формул:
Слайд 25
Закрепление понятий
Формула
площади квадрата
Формула
периметра квадрата
Формула
чётного числа
Назовите каждую из формул:
Слайд 26
Закрепление понятий
Формула
площади квадрата
Формула
периметра квадрата
Формула
чётного числа
Формула
длины
окружности через диаметр
Назовите каждую из формул:
Слайд 27
Закрепление понятий
Формула
площади квадрата
Формула
периметра квадрата
Формула
чётного числа
Формула
длины
окружности через диаметр
Формула
нечётного числа
Назовите каждую из формул:
Слайд 28
Закрепление понятий
Формула
площади квадрата
Формула
периметра квадрата
Формула
чётного числа
Формула
длины
окружности через диаметр
Формула
нечётного числа
Формула
нечётного числа
Назовите каждую
из формул:
Слайд 29
Изучение нового материала
Замените выражение суммой:
9 – 7 +
7 – 6 – 5 =
Слайд 30
Изучение нового материала
Замените выражение суммой:
9 –
7 + 7 – 6 – 5 =
=9 + (– 7) + 7 + (– 6) + (– 5)
Слайд 31
Изучение нового материала
Замените выражение суммой:
9 –
7 + 7 – 6 – 5 =
алгебраическая
сумма
=9 + (– 7) + 7 + (– 6) + (– 5)
Слайд 32
Изучение нового материала
Алгебраическая сумма – это запись, состоящая
из нескольких алгебраических выражений, соединенных
знаками «+» и «–».
Слайд 33
Стр. 32, № 42
Применение свойств арифметических
действий
1 выражение на выбор с последующей проверкой ответов
и указанием применяемых свойств действий
Слайд 34
Стр. 32, № 42
Применение свойств арифметических
действий
=10,407;
3) = – 9;
Слайд 35
Раскройте скобки устно:
Применение свойств арифметических действий
1) 5·(ху)
2)
5·(х+у)
3) – 5·(х+у)
4) – 5·(ху)
5) – 5·(х – у)
6)
– 5·(–х – у)
Слайд 36
Правила
раскрытия скобок в алгебраических выражениях
Стр. 30,31
Читаем, разбираем.
Работа
с теоретическим материалом.
Слайд 37
Стр.32, № 43
С устным комментированием
Слайд 38
Стр.32, № 43
С устным комментированием
Слайд 39
Стр.32, № 43
С устным комментированием
Слайд 40
Стр.32, № 43
С устным комментированием
Слайд 41
Стр.32, № 43
С устным комментированием
Слайд 42
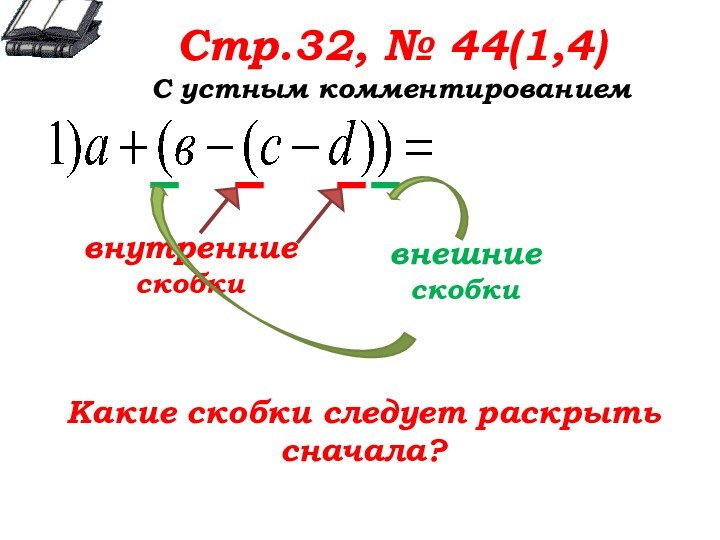
Стр.32, № 44(1,4)
С устным комментированием
Укажите внутренние и внешние
скобки
Слайд 43
Стр.32, № 44(1,4)
С устным комментированием
внутренние скобки
внешние
скобки
Какие
скобки следует раскрыть сначала?
Слайд 44
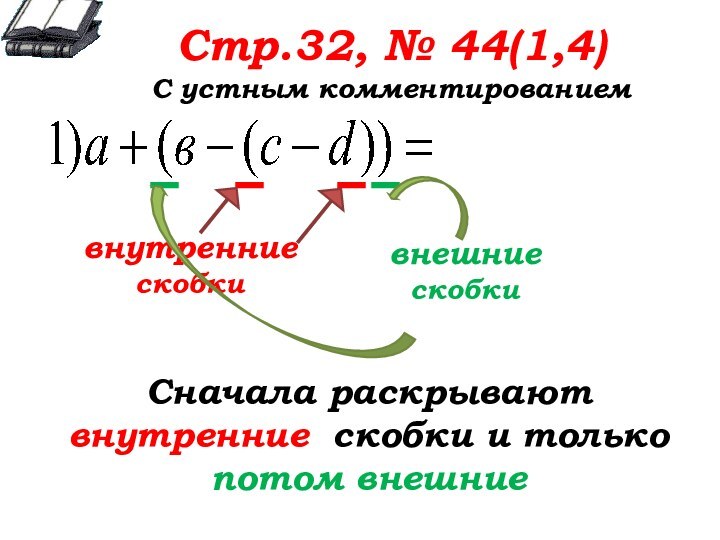
Стр.32, № 44(1,4)
С устным комментированием
внутренние скобки
внешние
скобки
Сначала
раскрывают внутренние скобки и только потом внешние
Слайд 45
Стр.32, № 44(1,4)
С устным комментированием
Теперь можно раскрыть и
внешние скобки
Слайд 46
Стр.32, № 44(1,4)
С устным комментированием
Слайд 47
Стр.32, № 44(4)
С устным комментированием
Слайд 48
Стр.32, № 44(4)
С устным комментированием
Слайд 49
Стр.32, № 44(4)
С устным комментированием
Слайд 50
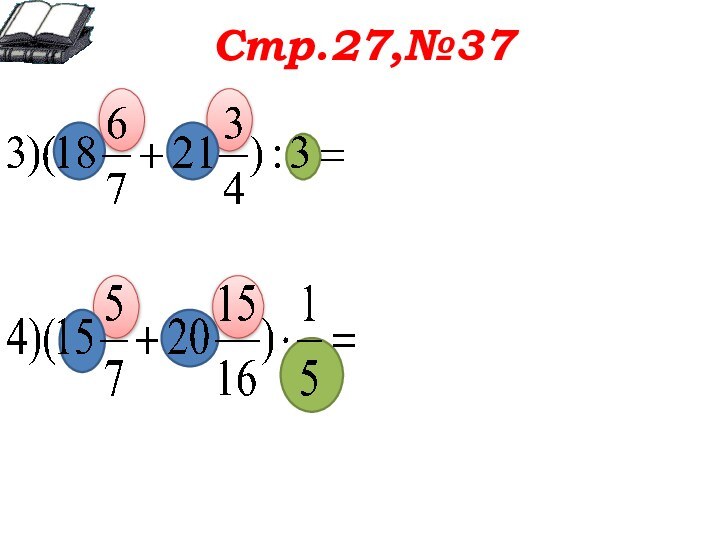
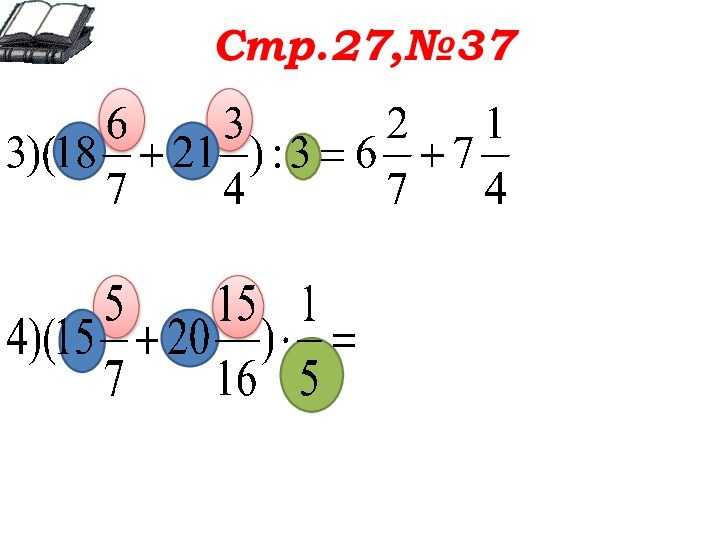
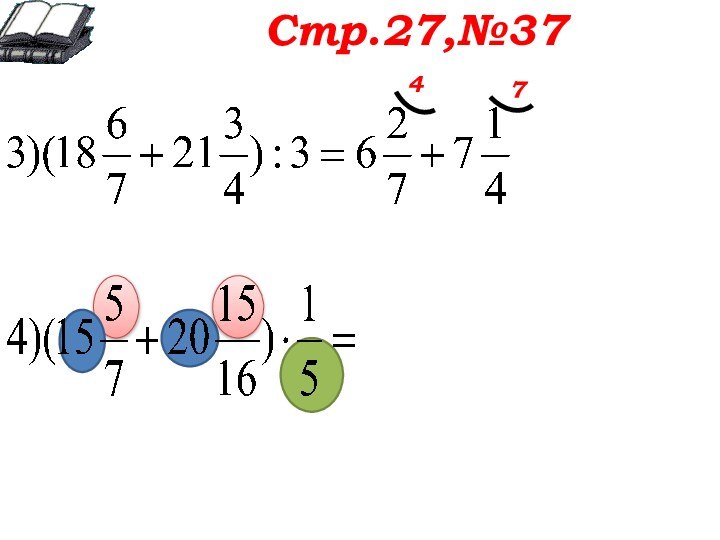
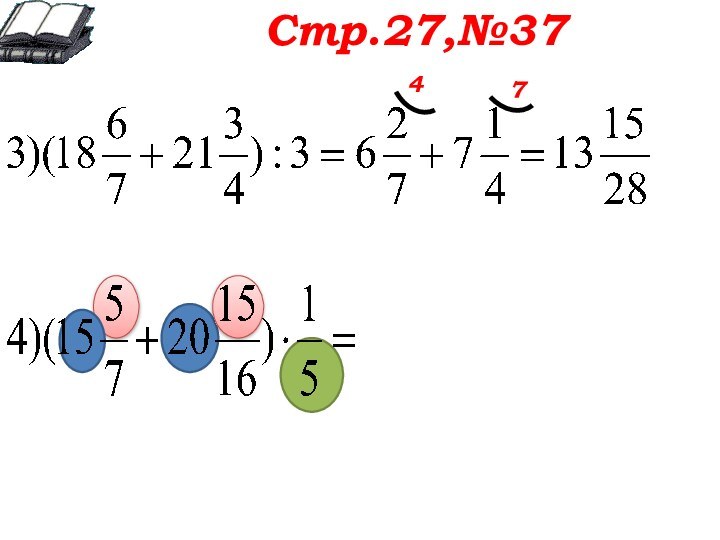
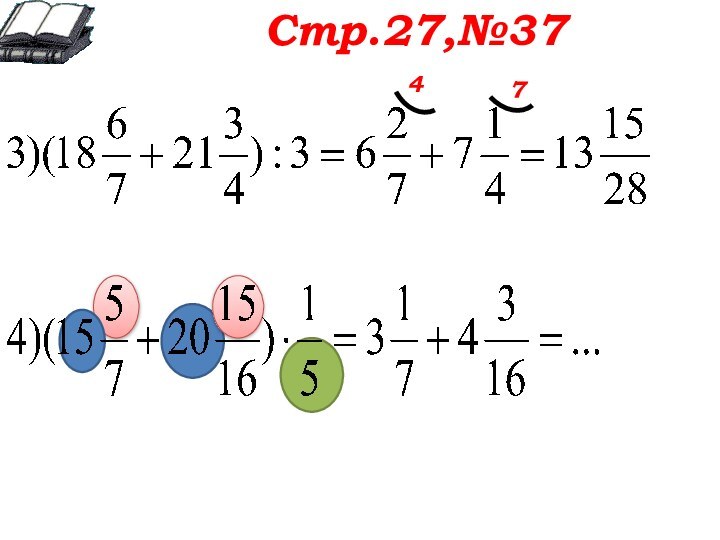
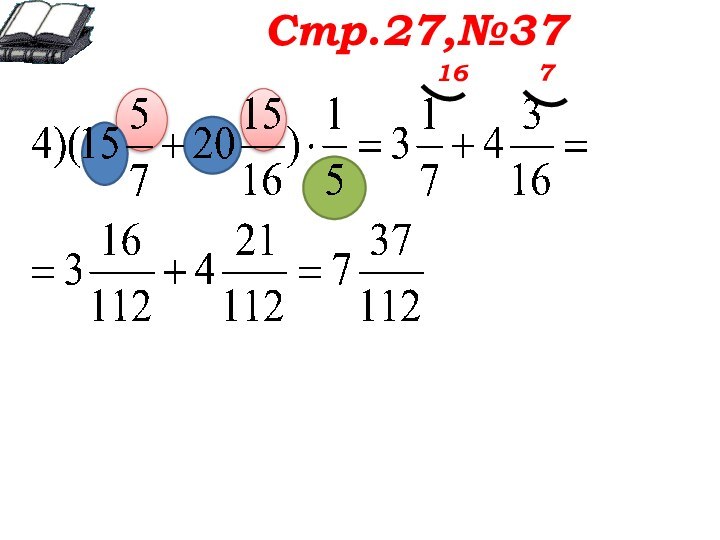
Стр.27,№37
Обсуждаем оба примера вместе
Слайд 57
Какие свойства удобно применять при упрощении выражений?
В
какой последовательности следует раскрывать скобки?
Итоги урока
Слайд 58
Итоги урока
Оцените свое настроение по итогам
урока:
Все понятно
Остались некоторые вопросы
Требуется
помощь
Итоги урока