последовательностей?
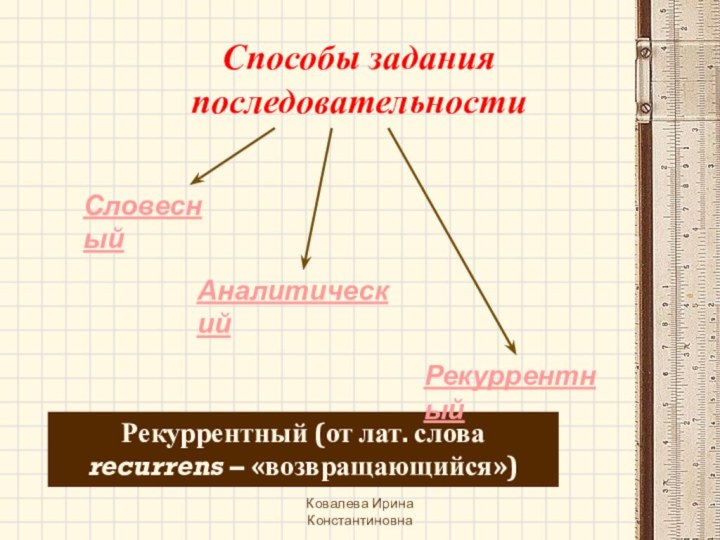
Как задаётся числовая последовательность?
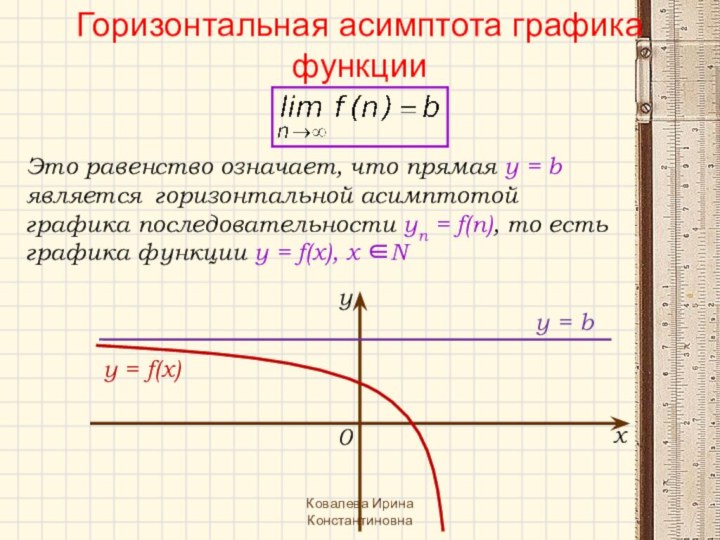
Что такое предел числовой
последовательности?Как находить предел числовой последовательности?
Ковалева Ирина Константиновна