- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему: История открытия комплексных чисел
Содержание
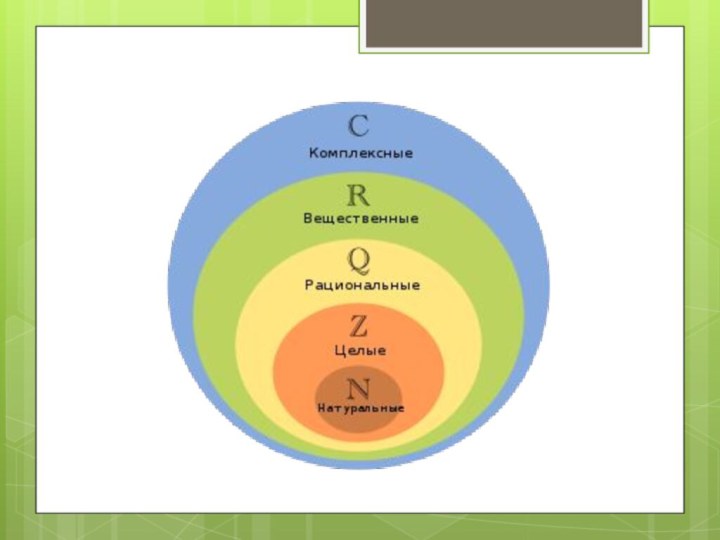
- 2. Понятие комплексных чиселКомплексное число — это выражение вида a + bi,
- 4. Арифметические действия над комплексными числами те же,
- 5. История созданияИсторически комплексные числа впервые были введены
- 6. Хотя согласно некоторым источникам, по-видимому, мнимые величины
- 7. Продолжительное время стоял вопрос, является ли множество
- 8. Символ для обозначения мнимой единицы предложил швейцарский, немецкий
- 9. Скачать презентацию
- 10. Похожие презентации
Понятие комплексных чиселКомплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это