Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по математике по теме Неравенства, подготовка к ОГЭ, часть1.

Содержание

НеравенстваПодготовка к экзамену 9 классВыполнила: Пестрецова Т.Г., учитель математики МБОУ «Чекмаревская ООШ»
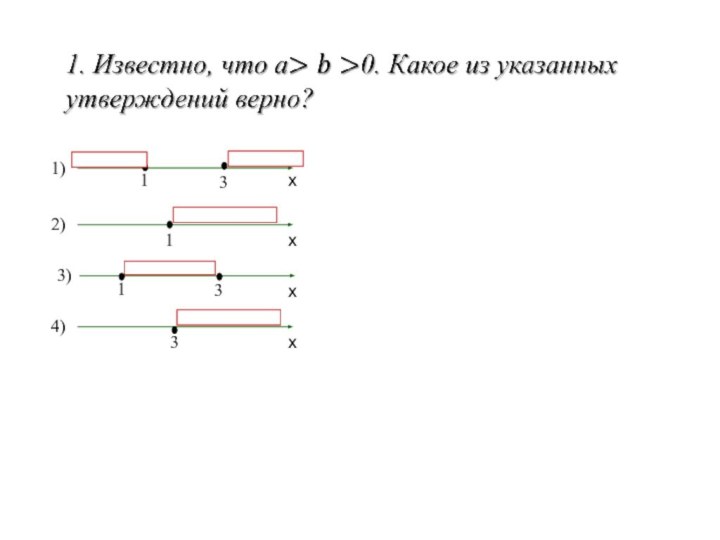
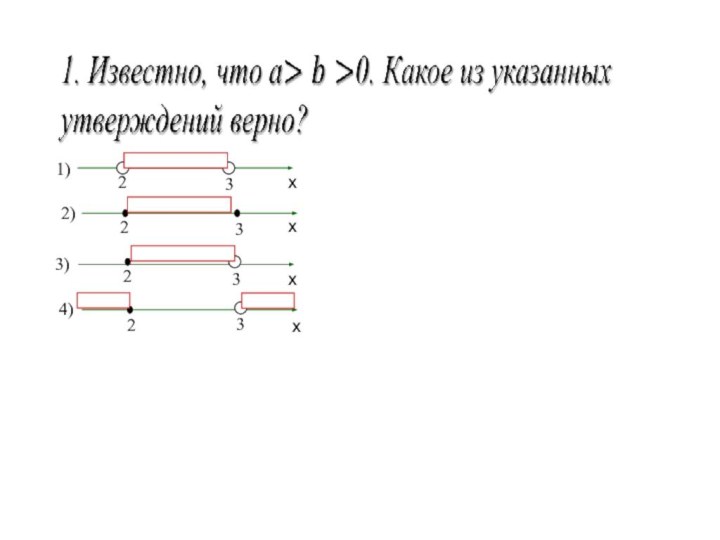
ерешнеи рвентсаевн НеравенстваПодготовка к экзамену 9 классВыполнила: Пестрецова Т.Г., Число а больше числа b, если разность а – b – положительное 1. Известно, что a > b. Сравните a - b и b Неравенство: Это соотношения вида f(x)>g(x), f(x) Виды неравенствЧисловое: а>b, где a и b- числаЛинейное: ax+b≤0, где a и 1. Сформулируйте свойства числовых неравенств.  2) - а > - b 3) 2b > 2а    2. На координатной прямой отмечены числа а и b.аb│0  3. На координатной прямой отмечено число а │││││││0123456ахКакое из утверждений относительно этого числа является верным?      1.Определение линейного неравенства2. Свойства неравенств с одной переменнойа) Можно переносить из одной 1. Какие неравенства соответствуют промежуткам?х ≥ 0 2. Изобразите геометрическую модель промежутков:  1)2)4)3)хххх- 1,5- 1,5- 0,5- 0,5 4)3)2)1)хххх    4. На каком рисунке изображено множество решений неравенства 4 – 7(х + 3)≤ - 9 1. Решите неравенство: 3(3x – 1) > 10x – 14 1) Системы неравенствСистема неравенств- это несколько неравенств с одной переменной.Решение системы неравенств- это  2)1)3)4) Система не имеет решений8998ххх  1)4)3)2)222-3-3 3-2хххх   Алгоритм решения квадратных неравенств ax2+bx+c>0 1. Находят дискриминант квадратного трехчлена ах2+вх+с Трехчлен не имеет корнейа > 0а < 0 3. Находят на оси Х промежутки, для которых точки параболы расположены выше 1. 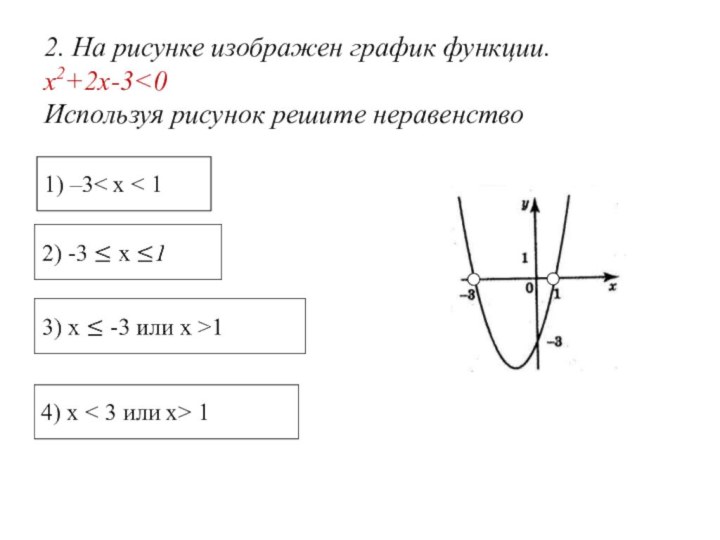Для каждого неравенства укажите множество его решений 4) (-1; 1) 2. На рисунке изображен график функции.x2+2x-3 1 3. Выберите из таблицы графическую интерпретацию для каждого из неравенств:4 4. Решите неравенство 1) (-∞ ;3] 2) (- ∞;9]3) [-3; 3]4) (- ∞;-3] [3;+ ∞)  5. Укажите неравенство, которое не имеет решений:      3)4)2)1)111333хххх Разложить многочлен на простые множители: (x-a)(x-b)>0найти корни многочлена; x- a=0  2)1)3)4)22223333хххх Самостоятельная работа1вариант2 вариант Ответы ДОМАШНЕЕ ЗАДАНИЕМой адрес: oboyan111@mail.ru Удачи на ГИА. Литература:1.Кузнецова Л.В., Суворова С.Б., Бунимович Е.А., Колесникова Т.В., Рослова Л.О. Сборник заданий
Слайды презентации

Слайд 2 Неравенства
Подготовка к экзамену

НеравенстваПодготовка к экзамену 9 классВыполнила: Пестрецова Т.Г., учитель математики МБОУ «Чекмаревская ООШ»

9 класс
Выполнила: Пестрецова Т.Г., учитель математики МБОУ «Чекмаревская ООШ»

Слайд 3 Число а больше числа b,
если разность а

Число а больше числа b, если разность а – b –

– b – положительное число
a > b, если а

– b > 0

Число а меньше числа b,
если разность а – b – отрицательное число
a < b, если а – b < 0

Если а – b = 0, то а = b

На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее

Слайд 4 1. Известно, что a > b. Сравните a

1. Известно, что a > b. Сравните a - b и

- b и b - a
1) a - b

> b - a

2) a - b < b - a

3) a - b = b - a

4) Данных для сравнения недостаточно.

2.О числах a, b, c и d известно, что a < b, b = c, d > c.
Сравните d и a.

1) d = a

2) d < a

3) d > a

4) Сравнить невозможно.

Слайд 5 Неравенство:
Это соотношения вида
f(x)>g(x), f(x)

Неравенство: Это соотношения вида f(x)>g(x), f(x)

или f(x) ≥g(x), f(x)≤ g(x)

строгие нестрогие
Решения неравенства- это значения переменной, обращающие его в верное числовое неравенство.
Решить неравенство- значит найти все решения или доказать, что их нет.



Слайд 6 Виды неравенств
Числовое: а>b, где a и b- числа
Линейное:

Виды неравенствЧисловое: а>b, где a и b- числаЛинейное: ax+b≤0, где a

ax+b≤0, где a и b- числа, х- переменная
Квадратное: ax2+bx+c>0

(неравенство II степени)
где a, b, c- числа, х- переменная
Неравенство вида: (x-a)(x-b)(x-c)>0
где a, b, c- числа, х- переменная

Слайд 7 1. Сформулируйте свойства числовых неравенств.








1. Сформулируйте свойства числовых неравенств.

Слайд 8  
2) - а > - b
3) 2b

 2) - а > - b 3) 2b > 2а   

> 2а
 
 

Слайд 9 2. На координатной прямой отмечены числа а и

2. На координатной прямой отмечены числа а и b.аb│0 

b.


а
b
│
0

 

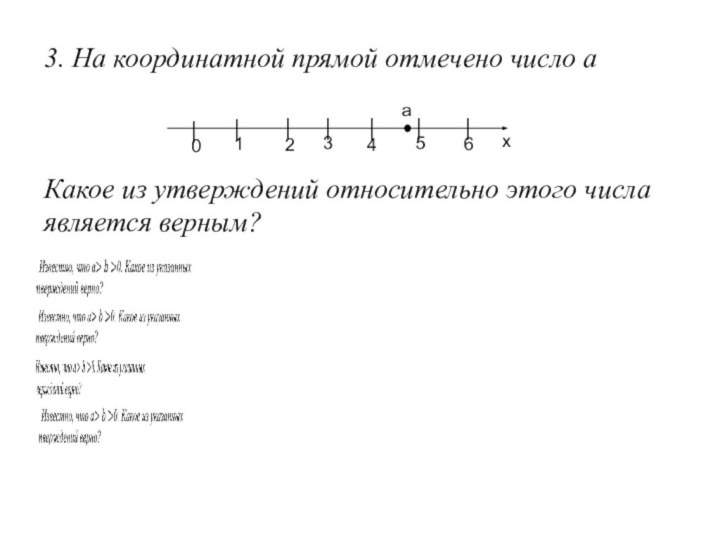
Слайд 10 3. На координатной прямой отмечено число а
│
│
│
│
│
│
│
0
1
2
3
4
5
6

а
х
Какое

3. На координатной прямой отмечено число а │││││││0123456ахКакое из утверждений относительно этого числа является верным?     

из утверждений относительно этого числа является верным?
 
 
 
 

Слайд 11 1.Определение линейного неравенства
2. Свойства неравенств с одной переменной
а)

1.Определение линейного неравенства2. Свойства неравенств с одной переменнойа) Можно переносить из

Можно переносить из одной части неравенства в другую, изменяя

знаки слагаемых.

б) Обе части неравенства можно умножать (делить) на одно и тоже отличное от нуля число.

:а



 

Слайд 12 1. Какие неравенства соответствуют
промежуткам?
х ≥ 0

1. Какие неравенства соответствуют промежуткам?х ≥ 0

Слайд 13 2. Изобразите геометрическую модель промежутков:

2. Изобразите геометрическую модель промежутков:

Слайд 14  
1)
2)
4)
3)




х
х
х
х
- 1,5
- 1,5
- 0,5
- 0,5




 1)2)4)3)хххх- 1,5- 1,5- 0,5- 0,5

Слайд 15 4)
3)
2)
1)




х
х
х
х
 
 
 
 




4. На каком рисунке изображено множество решений неравенства

4)3)2)1)хххх    4. На каком рисунке изображено множество решений неравенства 4 – 7(х + 3)≤ - 9

4 – 7(х + 3)≤ - 9

Слайд 16 1. Решите неравенство: 3(3x – 1) > 10x

1. Решите неравенство: 3(3x – 1) > 10x – 14 1)

– 14
1) (- ∞; 11)
2)

(11; + ∞)

3) (-∞; - 11)

4) (- 11; +∞)

2. Решите неравенство: 6 – 3x > 19 – (x – 7)

1) x > - 3

 

 

4) x < - 3

3. Решите неравенство: x + 4 ≥ 4x – 5 и укажите, на каком рисунке изображено множество его решений

1)

2)

3)

4)


-3


-3


3


3

4. Какое из следующих чисел не является решением неравенства 6x – 15 > 8x – 11?

1) - 1,8

2) - 2,6

3) - 3,7

4) - 8,9

МАЛЕНЬКИЙ ТЕСТ

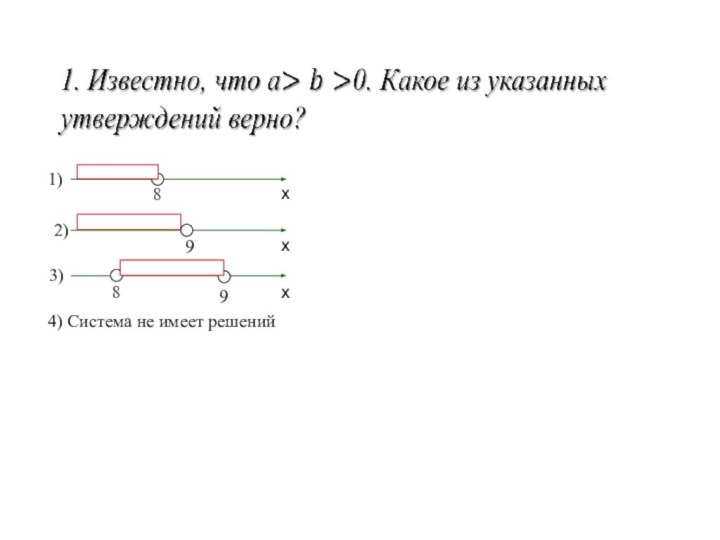
Слайд 17 Системы неравенств
Система неравенств- это несколько неравенств с одной

Системы неравенствСистема неравенств- это несколько неравенств с одной переменной.Решение системы неравенств-

переменной.
Решение системы неравенств- это значение переменной, при котором каждое

из неравенств системы обращается в верное числовое неравенство.
Общее решение неравенств- это множество всех решений системы неравенств.

Слайд 18  
2)
1)
3)
4) Система не имеет решений




8
9
9
8



х
х
х

 2)1)3)4) Система не имеет решений8998ххх

Слайд 19  
1)
4)
3)
2)







2
2
2
-3
-3
3
-2
х
х
х
х





 1)4)3)2)222-3-3 3-2хххх

Слайд 20  

 

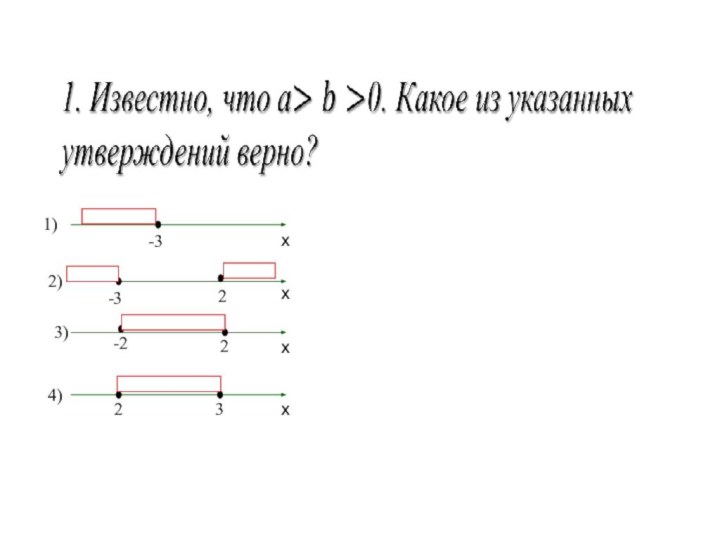
Слайд 21 Алгоритм решения квадратных неравенств ax2+bx+c>0
1. Находят

Алгоритм решения квадратных неравенств ax2+bx+c>0 1. Находят дискриминант квадратного трехчлена ах2+вх+с

дискриминант квадратного трехчлена ах2+вх+с и выясняют, имеет ли трехчлен

корни;
D >0, два корня х и х
D=0, один корень х
D<0 корней нет
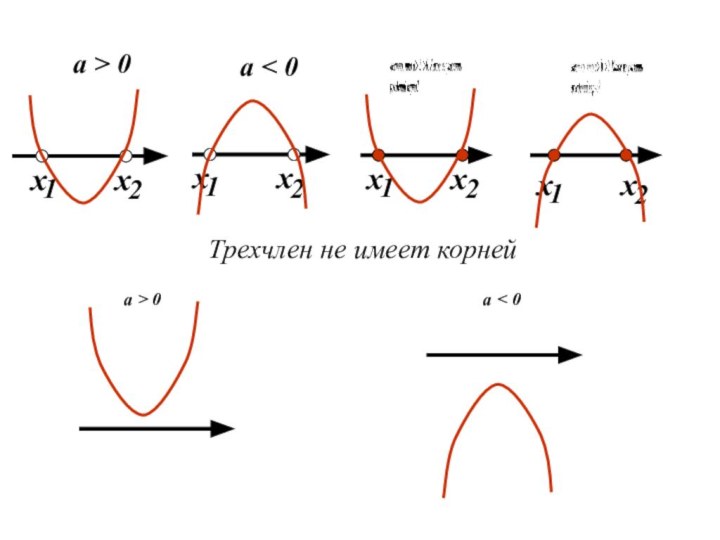
2. Если трехчлен имеет корни, то отмечают их на оси Х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а > 0 или вниз при а < 0; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а > 0 или в нижней при а< 0;

Слайд 22 Трехчлен не имеет корней
а > 0
а < 0


Трехчлен не имеет корнейа > 0а < 0

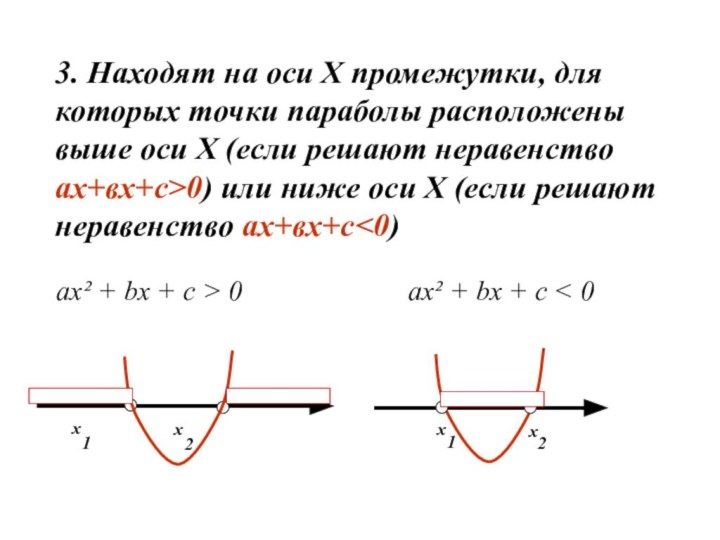
Слайд 23 3. Находят на оси Х промежутки, для которых

3. Находят на оси Х промежутки, для которых точки параболы расположены

точки параболы расположены выше оси Х (если решают неравенство

ах+вх+с>0) или ниже оси Х (если решают неравенство ах+вх+с<0)

aх² + bx + c > 0







х

х

х

х

1

1

2

2




aх² + bx + c < 0

Слайд 24 1. Для каждого неравенства укажите
множество его решений

1. Для каждого неравенства укажите множество его решений 4) (-1; 1)


4) (-1; 1)

Слайд 25 2. На рисунке изображен график функции.
x2+2x-3

2. На рисунке изображен график функции.x2+2x-3 1

неравенство
1) –3< x < 1
4) x < 3

или х> 1



Слайд 26 3. Выберите из таблицы графическую интерпретацию для каждого

3. Выберите из таблицы графическую интерпретацию для каждого из неравенств:4

из неравенств:






4

Слайд 27 4. Решите неравенство
 
1) (-∞ ;3]
2) (- ∞;9]
3)

4. Решите неравенство 1) (-∞ ;3] 2) (- ∞;9]3) [-3; 3]4) (- ∞;-3] [3;+ ∞) 

[-3; 3]
4) (- ∞;-3] [3;+ ∞)
 

Слайд 28 5. Укажите неравенство, которое не имеет решений:
 
 
 
 

5. Укажите неравенство, которое не имеет решений:    

Слайд 29  
3)
4)
2)
1)






1
1
1
3
3
3
х
х
х
х





 3)4)2)1)111333хххх

Слайд 30 Разложить многочлен на простые множители: (x-a)(x-b)>0
найти корни многочлена;

Разложить многочлен на простые множители: (x-a)(x-b)>0найти корни многочлена; x- a=0

x- a=0 x-

b=0
x=a x=b
изобразить их на числовой прямой;


разбить числовую прямую на интервалы;
определить знаки множителей на интервалах знакопостоянства;
выбрать промежутки нужного знака;
записать ответ (с помощью скобок или знаков неравенства).

Алгоритм решения методом интервалов






b

a

+

+

–

х

Слайд 31  
2)
1)
3)
4)








2
2
2
2
3
3
3
3





х
х
х
х

 2)1)3)4)22223333хххх

Слайд 32 Самостоятельная работа
1вариант

2 вариант

Самостоятельная работа1вариант2 вариант

Слайд 33 Ответы

Ответы

Слайд 34 ДОМАШНЕЕ ЗАДАНИЕ

Мой адрес: oboyan111@mail.ru

ДОМАШНЕЕ ЗАДАНИЕМой адрес: oboyan111@mail.ru

Слайд 35 Удачи на ГИА.

Удачи на ГИА.
  • Имя файла: prezentatsiya-po-matematike-po-teme-neravenstva-podgotovka-k-oge-chast1.pptx
  • Количество просмотров: 197
  • Количество скачиваний: 6
- Предыдущая Презентация по обществознанию на тему: Местное самоуправление (9 класс)
Следующая - Презентация Профилактика дисграфии и дислексии в подготовительном классе

Похожие презентации

Презентация по алгебре Иррациональные уравнения (8 класс) Презентация по алгебре Иррациональные уравнения (8 класс) 129
Рекурсия Рекурсия 180
Разложение многочлена на множители - Презентация Разложение многочлена на множители - Презентация 146
Квадратичная функция и её график Квадратичная функция и её график 139
Презентация к уроку геометрии Движения. Симметрия в пространстве Презентация к уроку геометрии Движения. Симметрия в пространстве 155
Презентация к уроку по теме Теорема Виета Презентация к уроку по теме Теорема Виета 162
Все действия с обыкновенными дробями Все действия с обыкновенными дробями 150
Элементы математической статистики Элементы математической статистики 186
Презентация по математике на тему Четные и нечетные функции Презентация по математике на тему Четные и нечетные функции 146
Квадратная функция и ее график Квадратная функция и ее график 135
Презентация по алгебре на тему:Решение задач с помощью систем уравнения Презентация по алгебре на тему:Решение задач с помощью систем уравнения 134
Диофантовы уравнения Диофантовы уравнения 180
Презентация Тригонометрические неравенства по алгебре 9 класс Презентация Тригонометрические неравенства по алгебре 9 класс 117
Построение диаграмм Построение диаграмм 155
Презентация по Теории вероятностей (11 класс) Презентация по Теории вероятностей (11 класс) 203
Формула корней квадратного уравнения. 8-й класс Формула корней квадратного уравнения. 8-й класс 195
Презентация к уроку математики по теме Квадрат суммы и разности двух выражений в 7 классе. Презентация к уроку математики по теме Квадрат суммы и разности двух выражений в 7 классе. 63
Параллельность прямых 7 класс Параллельность прямых 7 класс 155
Математика вокруг нас Математика вокруг нас 50
Решение квадратных уравнений по формуле Решение квадратных уравнений по формуле 143
Решение квадратных уравнений Решение квадратных уравнений 128
Презентация и конспект урока алгебры в 7 классе Возведение в квадрат суммы и разности двух выражений Презентация и конспект урока алгебры в 7 классе Возведение в квадрат суммы и разности двух выражений 219
Решение рациональных уравнений Решение рациональных уравнений 132
Натурал көрсеткішті дәреже және натурал көрсеткішті дәреженің қасиеттері тақырыбына презентация 7 сынып Натурал көрсеткішті дәреже және натурал көрсеткішті дәреженің қасиеттері тақырыбына презентация 7 сынып 268
Презентация по алгебре на тему Квадратные уравнения (8 класс) Презентация по алгебре на тему Квадратные уравнения (8 класс) 143
График функции 7 класс График функции 7 класс 133
Действия с многочленами Действия с многочленами 150
Презентация к уроку математики в 8 классе по теме: Функции и графики. Повторение. Презентация к уроку математики в 8 классе по теме: Функции и графики. Повторение. 83
Презентация по математике квадратный корень из произведения и дроби (8 класс) Презентация по математике квадратный корень из произведения и дроби (8 класс) 143
Алгебра: Кусочно-непрерывные функции (9 класс) Алгебра: Кусочно-непрерывные функции (9 класс) 179