- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Исследование функции с помощью производной (11 класс)
Содержание
- 2. ЦЕЛИ УРОКА:- Показать умение анализировать график функции
- 3. «Теория без практики мертва или бесплодна; практика
- 4. 1 этап – «Разведка боем»Итак, участники, внимание!Сформулируйте или продолжите математическое утверждение.
- 5. 1.Если f`(Х)>0 на промежутке, то …
- 6. 2.Точка Х0 , такая, что для всех
- 7. 3.Точки экстремума функции – это …
- 8. 4.Стационарные точки – это …
- 9. 5.Если f`(Х)
- 10. 6.Точкой минимума функции f(Х) называется такая точка Х0 , что …
- 11. 7.Необходимое условие экстремума (теорема Ферма): Если дифференцируемая
- 12. 8.Достаточное условие экстремума: если при переходе через
- 13. 9.Скорость Ѵ есть производная …
- 14. 10.Ускорение а есть производная …
- 15. 11.Геометрический смысл производной: …
- 16. 12.Если при переходе через стационарную точку Х0 производная меняет знак с «-» на «+», то …
- 17. 2 этап – «Точечные удары»Дан график функции
- 18. 1.Определите количество точек экстремума функции y = f(Х).
- 19. 2.Определите количество точек min функции y=f(x) на отрезке [-8;4].
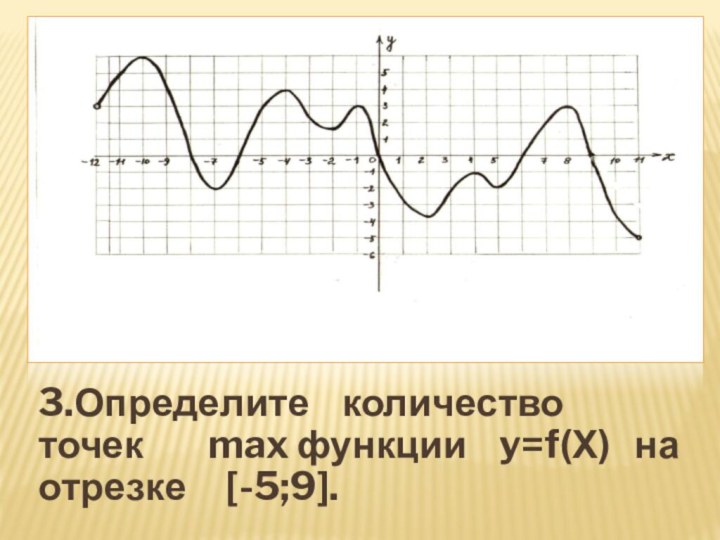
- 20. 3.Определите количество точек
- 21. 4.Найти сумму точек экстремума
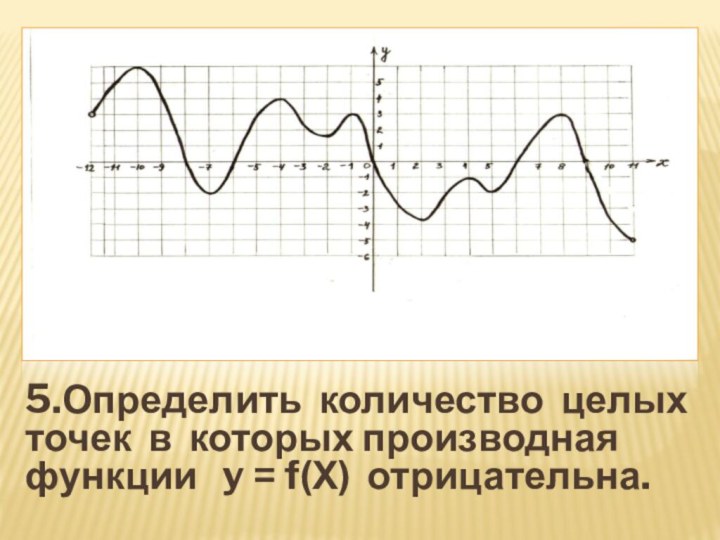
- 22. 5.Определить количество целых точек в которых производная функции y = f(Х) отрицательна.
- 23. 6.Найдите количество точек в
- 24. 7.Найдите промежутки возрастания функции у
- 25. 8.Укажите количество точек в которых производная функции f`(Х)=0.
- 26. 9.Найдите промежутки убывания функции у = f (Х). В ответ запишите длину наименьшего из них.
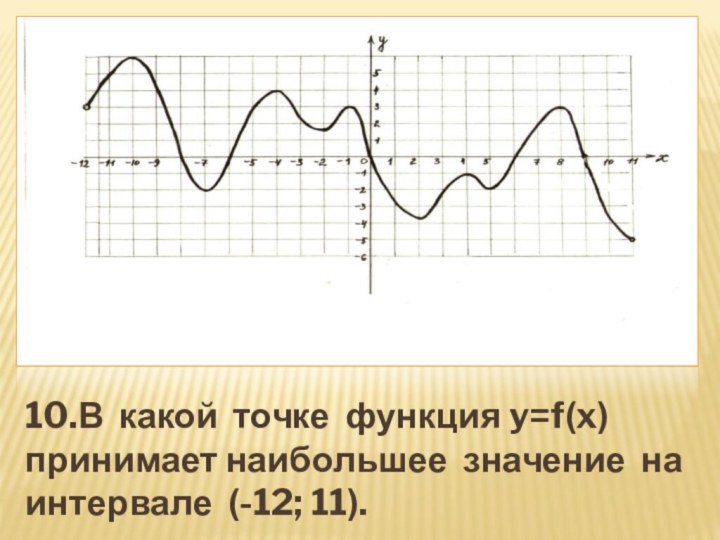
- 27. 10.В какой точке функция y=f(x) принимает наибольшее значение на интервале (-12; 11).
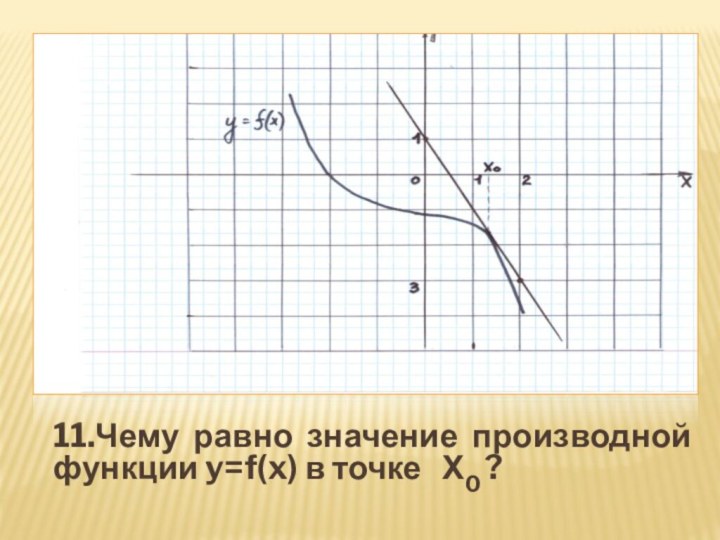
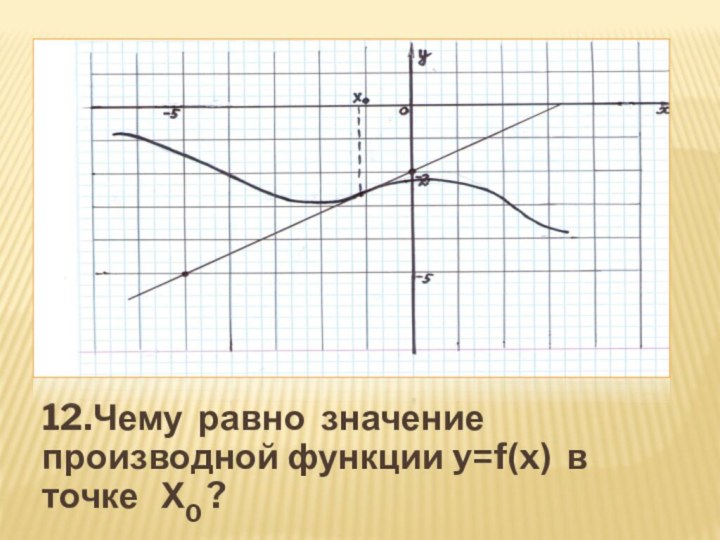
- 28. 11.Чему равно значение производной функции y=f(x) в точке Х0 ?
- 29. 12.Чему равно значение производной функции y=f(x) в точке Х0 ?
- 30. Ученики, ВНИМАНИЕ! Ответьте на следующие вопросы:
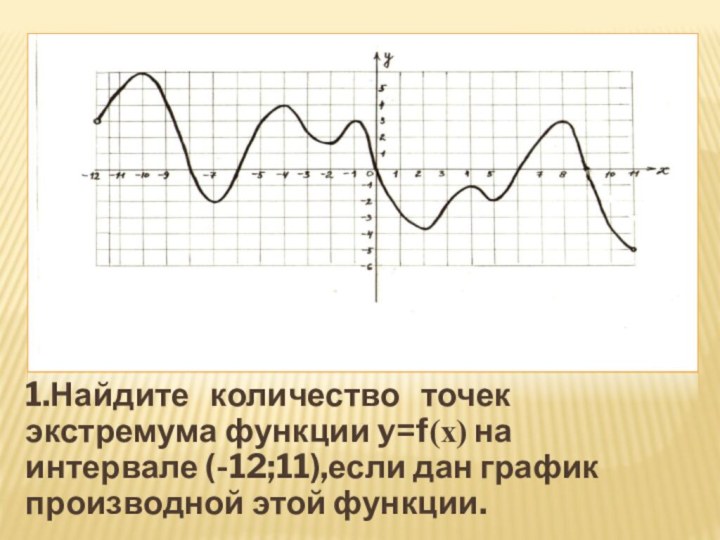
- 31. 1.Найдите количество точек экстремума
- 32. 2.Найдите промежутки возрастания функции y=f(Х). В ответе
- 33. 3.Найдите промежутки убывания функции y=f(Х). В
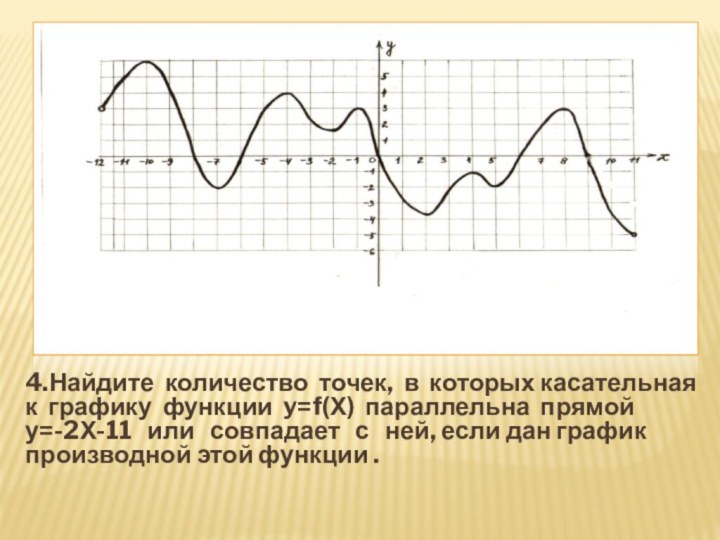
- 34. 4.Найдите количество точек, в которых касательная к
- 35. 5.Найдите количество точек max
- 36. 6.Найдите количество точек
- 37. 7.В какой точке функция y=f(Х) принимает
- 38. 8.В какой точке отрезка [-6; -1] функция
- 39. 9.В какой точке отрезка [1; 5] функция принимает наибольшее значение,если дан график производной этой функции.
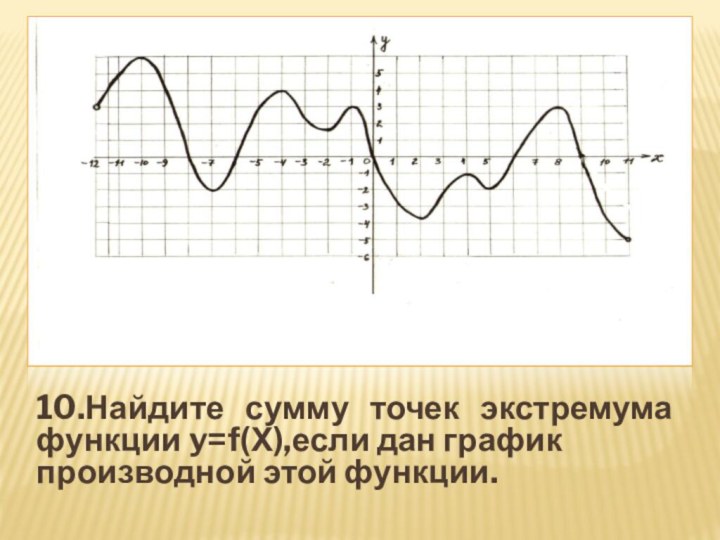
- 40. 10.Найдите сумму точек экстремума функции y=f(Х),если дан график производной этой функции.
- 41. 11.Найдите количество точек, в которых производная функции f`(Х)=0, если дан график производной этой функции.
- 42. 12.Найдите наибольшую абсциссу точки, в которой касательная
- 43. 4 этап – «Быстрый штурм»А теперь решаем задачи письменно*)
- 44. Скачать презентацию
- 45. Похожие презентации
ЦЕЛИ УРОКА:- Показать умение анализировать график функции с помощью применения производнойРазвивать быстроту мысли, внимательность и смекалкуВоспитание таких чувств как активность, взаимопомощь и самостоятельность


















![Презентация по математике на тему Исследование функции с помощью производной (11 класс) 2.Определите количество точек min функции y=f(x) на отрезке [-8;4].](/img/tmb/7/665030/18a5d831e7b6b079c2150626384a7fff-720x.jpg)











![Презентация по математике на тему Исследование функции с помощью производной (11 класс) 8.В какой точке отрезка [-6; -1] функция y=f(Х) принимает наименьшее значение ,](/img/tmb/7/665030/1b1bb59ad90703f8ba8fd2055875a91b-720x.jpg)
![Презентация по математике на тему Исследование функции с помощью производной (11 класс) 9.В какой точке отрезка [1; 5] функция принимает наибольшее значение,если дан график производной этой функции.](/img/tmb/7/665030/186e717f5cc901686087f5c88d560850-720x.jpg)




Слайд 2
ЦЕЛИ УРОКА:
- Показать умение анализировать график функции с
помощью применения производной
чувств как активность, взаимопомощь и самостоятельность
Слайд 3
«Теория без практики мертва или бесплодна; практика без
теории невозможна и пагубна. Для теории нужны знания, для
практики, сверх всего, - и умения».Алексей Николаевич Крылов
(русский ученый-инженер)





























