Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Биномиальное распределение

Содержание

Случайную величину Х, распределенную по биномиальному закону, можно трактовать следующим образом:Рассмотрим событие А, которое происходит в опыте с вероятностью р и не происходит с вероятностью q=1-p. Производится серия из n опытов в одинаковых условиях и независимо
15. Биномиальное распределениегде q=1-p.Случайная величина Х называется распределенной по биномиальному закону с Случайную величину Х, распределенную по биномиальному закону, можно трактовать следующим образом:Рассмотрим событие Составить ряд распределения величины, распределенной по биномиальному закону с параметрами n=4, р=1/3.ПРИМЕР. Производится серия из n=4 опытов. Случайная величина Х - число опытов, в Вероятность того, что событие А произойдет в одном опыте (m=1):Аналогично находим вероятности Можно убедиться, что суммарная вероятность действительно равна 1. Таким образом, ряд распределения Найдем математическое ожидание случайной величины, распределенной по биномиальному закону.Х - число опытов Тогда математическое ожидание случайной величины Х:M[X]=M[Z1]+M[Z2]+…+M[Zn]Найдем математическое ожидание ZiРяд распределения Zi имеет Найдем дисперсию случайной величины ZiТак как случайные величины Zi независимы, тоТаким образом,
Слайды презентации

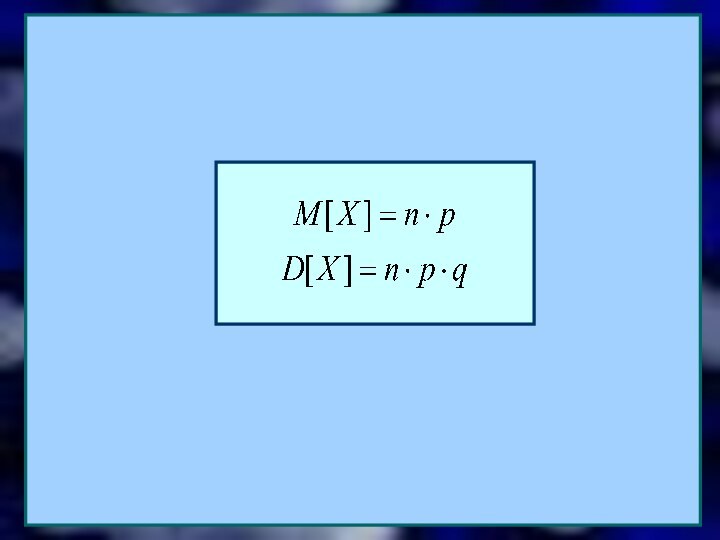
Слайд 2
Случайную величину Х, распределенную по биномиальному закону, можно

Случайную величину Х, распределенную по биномиальному закону, можно трактовать следующим образом:Рассмотрим

трактовать следующим образом:
Рассмотрим событие А, которое происходит в опыте

с вероятностью р и не происходит с вероятностью q=1-p. Производится серия из n опытов в одинаковых условиях и независимо друг от друга. Случайная величина Х - сколько раз событие А произошло в данной серии опытов.

Слайд 3
Составить ряд распределения величины, распределенной по биномиальному закону

Составить ряд распределения величины, распределенной по биномиальному закону с параметрами n=4, р=1/3.ПРИМЕР.

с параметрами n=4, р=1/3.
ПРИМЕР.

Слайд 4
Производится серия из n=4 опытов. Случайная величина Х

Производится серия из n=4 опытов. Случайная величина Х - число опытов,

- число опытов, в которых может произойти событие А,

может принимать значения 0, 1, 2, 3, 4.

Соответствующие вероятности находятся по формуле Бернулли при n=4, p=1/3, q=1-1/3=2/3.

Решение:

Вероятность того, что событие А не произойдет ни в одном опыте (m=0):

Слайд 5
Вероятность того, что событие А произойдет
в

Вероятность того, что событие А произойдет в одном опыте (m=1):Аналогично находим

одном опыте (m=1):
Аналогично находим вероятности того, что это событие

произойдет в двух (m=2), в трех (m=3) и в четырех (m=4) опытах:

Слайд 6
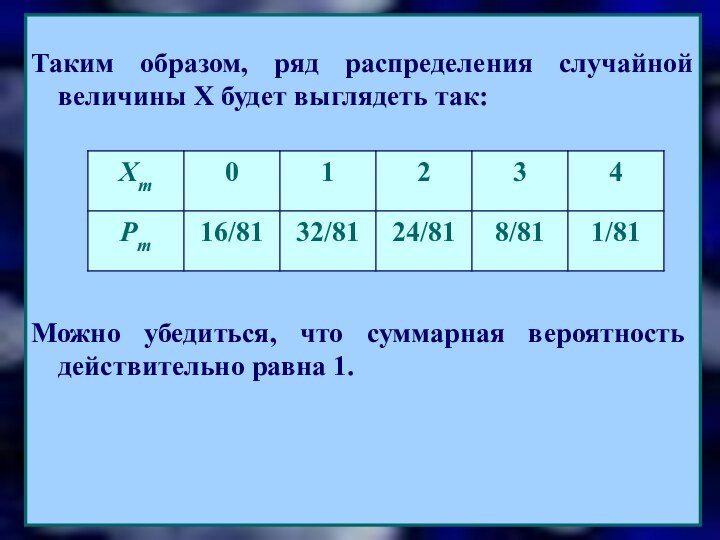
Можно убедиться, что суммарная вероятность действительно равна 1.

Можно убедиться, что суммарная вероятность действительно равна 1. Таким образом, ряд


Таким образом, ряд распределения случайной величины Х будет выглядеть

так:

Слайд 7
Найдем математическое ожидание случайной величины, распределенной по биномиальному

Найдем математическое ожидание случайной величины, распределенной по биномиальному закону.Х - число

закону.
Х - число опытов в серии из n, в

которых произошло событие А.

Введем для каждого i=1,2…n случайную величину Zi .

Пусть Zi принимает всего два значения: 1 - если событие А произойдет в i-ом опыте и 0 - если событие А не произойдет в i-ом опыте.

Тогда событие Х выразится через сумму событий Zi :
Х= Z1 +Z2 +…+Zn

Слайд 8
Тогда математическое ожидание случайной величины Х:
M[X]=M[Z1]+M[Z2]+…+M[Zn]
Найдем математическое ожидание

Тогда математическое ожидание случайной величины Х:M[X]=M[Z1]+M[Z2]+…+M[Zn]Найдем математическое ожидание ZiРяд распределения Zi

Zi
Ряд распределения Zi имеет вид:
Тогда M[Zi ]=p и M[X]=np.

Слайд 9
Найдем дисперсию случайной величины Zi
Так как случайные величины

Найдем дисперсию случайной величины ZiТак как случайные величины Zi независимы, тоТаким

Zi независимы, то
Таким образом, для случайной величины,
распределенной по

биномиальному закону,
  • Имя файла: binomialnoe-raspredelenie.pptx
  • Количество просмотров: 198
  • Количество скачиваний: 2
- Предыдущая Служебные части речи. Предлог
Следующая - Об основах охраны здоровья граждан в Российской Федерации

Похожие презентации

Степень с целым показателем Степень с целым показателем 123
Применение производной функции Применение производной функции 141
Корень n-й степени. посторение. презентация Корень n-й степени. посторение. презентация 192
вынесение множителя за знак корня и внесение множителя под знак корня(8 класс) вынесение множителя за знак корня и внесение множителя под знак корня(8 класс) 180
Производные в физике Производные в физике 158
Деление чисел Деление чисел 158
Уравнения Уравнения 192
Презентация по теме Сфера Презентация по теме Сфера 159
Разработка урока по теме Логарифмическая функция Разработка урока по теме Логарифмическая функция 185
Система уравнений Система уравнений 181
Презентация по математике 8 класс Кто хочет стать миллионером Презентация по математике 8 класс Кто хочет стать миллионером 158
Презентация по математике на тему Применение производной (1 курс Организация перевозок и управление на транспорте) Презентация по математике на тему Применение производной (1 курс Организация перевозок и управление на транспорте) 180
Презентация к уроку - КВН в 9 классе по теме: Решение задач с помощью систем уравнений Презентация к уроку - КВН в 9 классе по теме: Решение задач с помощью систем уравнений 168
Презентация к научно-исследовательской работе по теме Статистика как зеркало жизни Презентация к научно-исследовательской работе по теме Статистика как зеркало жизни 173
Презентация по математике Решение квадратных уравнений Презентация по математике Решение квадратных уравнений 160
Презентация по математике на тему Дробно-линейная функция (9 класс) Презентация по математике на тему Дробно-линейная функция (9 класс) 222
Презентация к уроку по алгебреСтепень с натуральным показателем Презентация к уроку по алгебреСтепень с натуральным показателем 153
Презентация по теме Решение задач с помощью дробных рациональных уравнений Презентация по теме Решение задач с помощью дробных рациональных уравнений 180
Презентация к уроку по алгебре в 9 классе Неравества 2 степени с одной переменной Презентация к уроку по алгебре в 9 классе Неравества 2 степени с одной переменной 151
Алгоритм решения неравенств Алгоритм решения неравенств 169
Производные в физике Производные в физике 163
Презентация по математике Преобразование выражений с помощью формул сокращенного умножения Презентация по математике Преобразование выражений с помощью формул сокращенного умножения 401
погрешность погрешность 190
Презентация по алгебре на темуКвадратные уравнения(8класс) Презентация по алгебре на темуКвадратные уравнения(8класс) 185
Презентация по алгебре на тему Решение квадратных уравнений (8 класс) Презентация по алгебре на тему Решение квадратных уравнений (8 класс) 164
Презентация по алгебре на тему : Чтение графика функции Презентация по алгебре на тему : Чтение графика функции 165
Презентация по математике на тему Лемниската Бернулли Презентация по математике на тему Лемниската Бернулли 224
Презентация к уроку обобщение и систематизация знаний по теме Решение уравнений в 9 классе. Презентация к уроку обобщение и систематизация знаний по теме Решение уравнений в 9 классе. 223
Дидактическая игра на тему ВПР Линейные уравнения Дидактическая игра на тему ВПР Линейные уравнения 194
Открытый урок алгебры в 9 классе по теме:Арифметическая и геометрическая прогрессии- урок систематизации и обобщения. Открытый урок алгебры в 9 классе по теме:Арифметическая и геометрическая прогрессии- урок систематизации и обобщения. 259