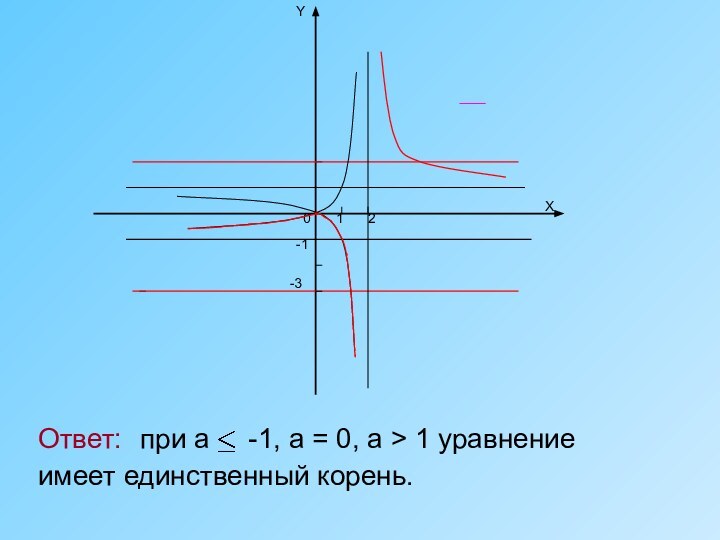
дробей, входящих в уравнение;
2. умножить обе части уравнения на
общий знаменатель;3. решить получившееся целое уравнение;
4. исключить из его корней те, которые обращают в нуль общий знаменатель.