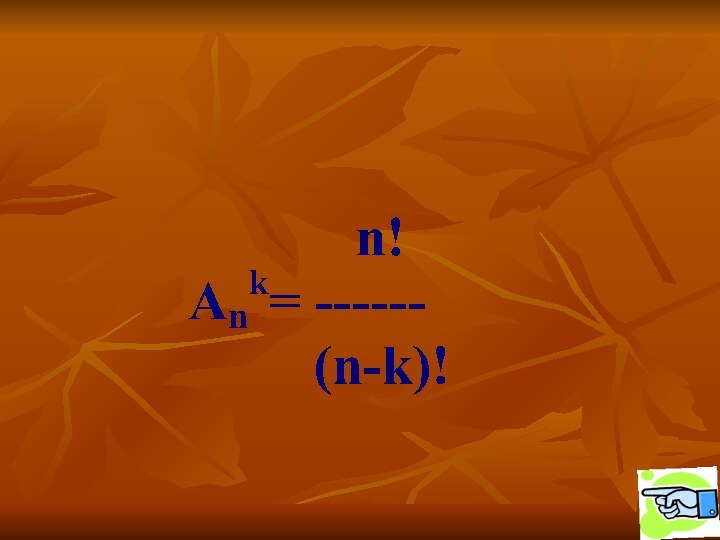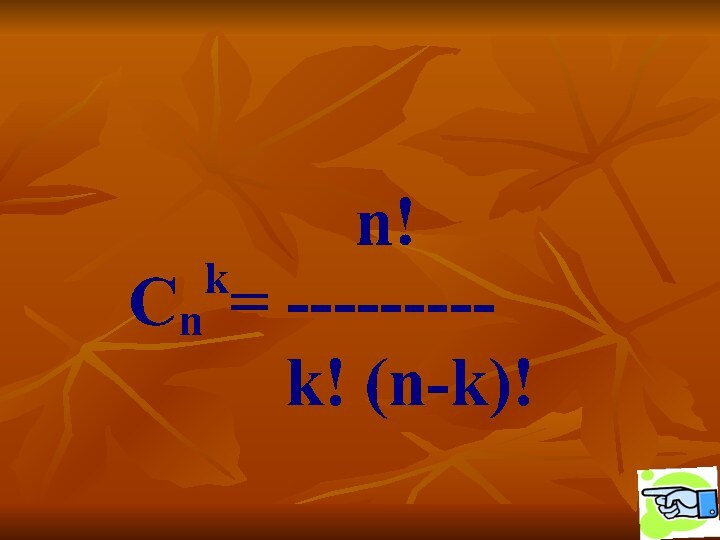Сколькими способами тренер может выбрать из них для предстоящего
турнира : а) команду из четырёх человек;
б) команду из четырёх человек, указав при этом, кто из членов команды будет играть на первой, второй, третьей и четвёртой досках?
№2 У Антона 6 друзей. Он может пригласить в гости одного или несколько из них. Определите общее число возможных вариантов.
№3 В 9 «а» классе учатся 25 учащихся, в 9 «б» - 20 учащихся, а в 9 «в» - 18 учащихся. Для работы на пришкольном участке надо выделить трёх учащихся из 9 «а», двух -из 9 «б» и одного – из 9 «в». Сколько существует способов выбора учащихся для работы на пришкольном участке?
С №1 Пять мальчиков и четыре девочки хотят сесть на девятиместную скамейку так, чтобы каждая девочка сидела между двумя мальчиками. Сколькими способами они могут это сделать?
№2 Из 12 солдат, в число которых входят Иванов и Петров, надо отправить в наряд трёх человек. Сколькими способами это можно сделать, если: а) Иванов и Петров должны пойти в наряд обязательно; б) Иванов и Петров должны остаться; в)Иванов
должен пойти в наряд, а Петров –остаться?
(Ответы)
Устал - отдохни