Слайд 2
1.Введение
2.Основное содержание:
Из биографии Пифагора.
Пифагорейская школа.
Теорема Пифагора и способы
её доказательства:
Простейшее доказательство.
Доказательство Эйнштейна.
Древнекитайское доказательство.
Древнеиндийское доказательство.
Доказательство Евклида.
Алгебраическое доказательство.
Векторное доказательство.
Применение
данной теоремы.
Великие тайны теоремы.
3.Выводы.
4.Библиография
содержание
Слайд 3
рассмотреть область ее применения.
Цели работы:
посмотреть,
в чем кроется популярность великого математика Пифагора;
открыть тайны теоремы
Пифагора через разбор истории теоремы;
разобраться в разных способах доказательств
теоремы;
Слайд 4
изучить и проанализировать литературу по данному вопросу;
познакомиться с
биографией великого ученого;
пронаблюдать за историей создания теоремы Пифагора;
объяснить великие
тайны теоремы Пифагора;
рассмотреть разные способы доказательств теоремы Пифагора, ее применение.
Задачи:
Слайд 5
Изучить теоретические сведения по исследуемой проблеме.
2. Сделать
анализ литературных источников (книг).
3. Провести социологический опрос среди людей
старшего поколения с целью выявить, какое количество доказательств знают не учёные и не исследователи данного вопроса, а обыкновенные люди.
Методы исследования:
Слайд 6
Пифагор – самая загадочная личность, человек-символ, философ, пророк.
Пифагор
– едва ли не самый популярный ученый за всю
историю человечества. Ни одно имя ученого не повторяется так часто.
Слайд 7
Великий ученый Пифагор родился около 570 г. до
н.э. Отцом Пифагора был Мнесарх, резчик по драгоценным камням.
Когда отец Пифагора был в Дельфах по своим торговым делам, он и его жена Партенис решили спросить у Дельфийского оракула, будет ли Судьба благоприятствовать им во время обратного путешествия в Сирию. Пифия (прорицательница Аполлона), сидя на золотом триоде над сияющим отверстием оракула, не ответила на их вопрос, но сказала Мнесарху, что его жена носит в себе дитя и что у них родится сын, который превзойдет всех людей в красоте и мудрости и который много потрудится в жизни на благо человечества.
По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.
Слайд 8
Древнегреческий философ, математик, астроном. Основатель пифагорейской школы в
Кротоне. Считался одним из самых образованных людей своего времени.
Доказал знаменитую теорему «О равенстве квадрата гипотенузы прямоугольного треугольника сумме квадратов катетов», которая носит теперь его имя. Обосновал многие свойства геометрических фигур. Разработал математическую теорию чисел и их пропорций. Внёс значительный вклад в развитие астрономии и акустики. Предположил, что движение небесных тел подчиняется определённым математическим законам. В своих трудах опирался на идеи мировой гармонии. Автор «Золотых стихов». Одна из основных заповедей Пифагора: «Не делай никогда того, чего не знаешь. Но научись всему, что следует знать».
Слайд 10
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства,

тайного монашеского ордена, члены которого обязывались вести «пифагорейский образ
жизни». Это был одновременно и религиозный союз, и политический клуб, и научное общество. Не только сила личности и мудрость Пифагора, но и высокая нравственность проповедуемых им идей и жизненных принципов притягивала к нему единомышленников. В основе религиозно-философского учения Пифагора лежало представление о числе, как основе всего существующего в мире. «Числа – суть боги на земле», – говорил он. Ритуал посвящения в члены пифагорейского братства был окружен множеством таинств, разглашение которых сурово каралось. Обучение в школе было двухступенчатое. Одни ученики назывались «математиками», т. е. познавателями, а другие – «акусматиками», т. е. слушателями. Математики – те, кто изучал суть науки, акусматики – те, кто прослушивал обобщенный свод знаний. Акусматики представляли первую ступень в школе Пифагора. Наиболее одаренные акусматики переводились в математики, им разрешалось видеть учителя, вести с ним научные споры. Пифагорейцы узнавали друг друга по звездчатому пятиугольнику – пентаграмме. Они верили, что в числовых закономерностях спрятана тайна мира. Мир чисел жил для пифагорейца особой жизнью, числа имели свой особый жизненный смысл.
Слайд 11
Каждое число в представлении пифагорейцев имело свой характер

и свои особые свойства. Так, например, нечётные числа считались
сильнее чётных, поскольку чётные делились пополам без остатка, а нечётные при таком делении всегда оставляли «про запас» единицу.
«Двойка воспринималась как женское число, а тройка – как мужское.
Символом супружества была пятёрка, а дружбу осеняло число восемь.
Число четыре было для них символом гармонии и здоровья, хранило ключ к соразмерности, поскольку включало в себя первые четыре числа. Позже оно стало символизировать четыре материальных элемента: землю, воздух, огонь и воду.
Девятка заведовала постоянством, это объясняли тем, например, что все кратные ей числа дают сумму цифр, равную девяти.
Шестёрка – символически напоминала о сотворении мира и считалась олицетворением совершенства. Также она являлась символом воли и неутомимости.
Семёрке приписывались удача, счастливый случай, пророческие сновидения, покровительство. И так далее.
Числа от 1 до 10 имеют, по Пифагору, связь со всеми жизненными проявлениями, обладают таинственной силой. Числам соответствуют буквы. Буквы складываются в слова, фразы. Так что у каждого слова существует ещё и цифровое значение, как бы усиливающее его смысл.
Слайд 12
«Пифагор впервые ввёл термин «философ», определив его как
«тот, кто пытается найти, выяснить»». А слово «мудрец» было
ему не по душе.
В своде «Пифагоровых законов и нравственных правил» есть такие изречения:
«Не почитай знания за одно с мудростью»,
«Тело своё не делай гробом души»,
«Если не можешь иметь верного друга, будь сам себе другом»,
«Не гоняйся за счастьем: оно всегда находится в тебе самом».
«Что есть мудрость? Знание порядка. Если желаешь быть мудрым в течение твоей жизни, всё поставь на своём месте. Преходящая временная слава не стоит тихого и безмятежного порядка, видимого в ежедневных трудах мудрого».
...Прошло 20 лет. Слава о братстве разнеслась по всему миру.
Слайд 13
Не найти никакой другой теоремы, имеющей столько всевозможных

названий. Во Франции и Германии в Средневековье теорему Пифагора
называли «мостом ослов» или «бегством убогих», потому что перед экзаменом, содержащим вопросы по этой теме, начинался массовый отток нерадивых студентов. У математиков арабского Востока эта теорема получило интересное название – «теорема невесты». Дело в том, что в некоторых списках «Начал» Эвклида эта теорема называлась «теоремой нимфы» за сходство чертежа с пчёлкой, бабочкой (по-гречески – «нимфа»). Но словом «нимфа» греки называли ещё и некоторых богинь, а также молодых женщин и невест.
При переводе с греческого арабский переводчик, не обратив внимания на чертёж, перевёл слово «нимфа» как «невеста», а не как «бабочка». Так появилось ласковое название знаменитой теоремы Пифагора – «теорема невесты».
Существует легенда, что когда Пифагор Самосский доказал свою теорему, он отблагодарил богов, принеся в жертву 100 быков».
Возможно, отсюда следует и ещё одно название знаменитой теоремы Пифагора – «теорема 100 быков»…
Слайд 14
Если дан нам треугольник
И притом с
прямым углом, То квадрат гипотенузы Мы всегда легко найдем : Катеты в квадрат возводим, Сумму степеней находим — И таким простым путем К результату мы придем.
Слайд 15
Теорема Пифагора – важнейшее утверждение геометрии. Ее открытие
приписывают древнегреческому философу и математику Пифагору Самосскому (VI в.
до н.э.). Но изучение вавилонских клинописных таблиц и древних китайских рукописей (копий ещё более древних манускриптов) показало, что знаменитая теорема была известна задолго до Пифагора, возможно, за несколько тысячелетий до него. Заслуга же Пифагора состояла в том, что учёный первым открыл доказательство этой теоремы. Открытие теоремы Пифагором окружено множеством красивых легенд. Со времён Пифагора появилось несколько сотен доказательств (более 350) его знаменитой теоремы, так что она даже попала в Книгу рекордов Гиннеса.
Слайд 16
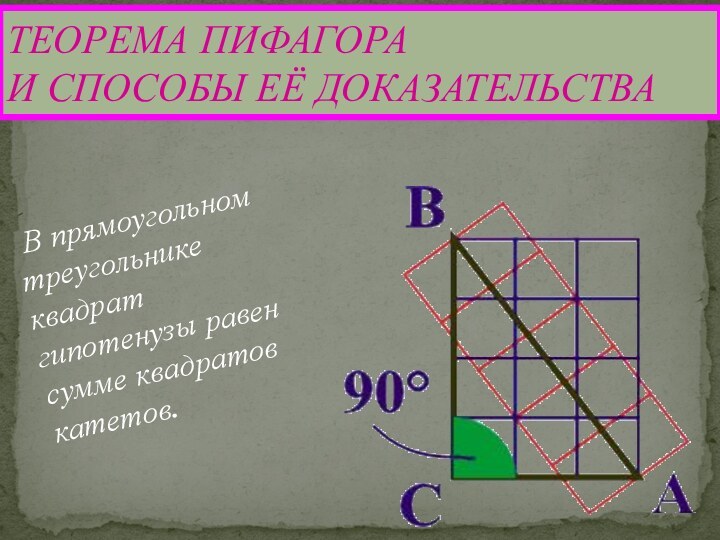
ТЕОРЕМА ПИФАГОРА
И СПОСОБЫ
ЕЁ ДОКАЗАТЕЛЬСТВА
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Слайд 17
У Евклида эта теорема гласит (дословный перевод):

"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".
Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ), сделанный Герхардом Клемонским (начало XII в.), в переводе на русский гласит: "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".
В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так : "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".
В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".
Более строгой надо считать такую формулировку: «Если гипотенуза и катеты прямоугольного треугольника измерены одной и той же единицей длины, то квадрат числового значения длины гипотенузы равен сумме квадратов числовых значений длин катетов».
Формулировки теоремы
Слайд 18
Различные способы доказательства
теоремы Пифагора
На рисунке дан простейший равнобедренный прямоугольный треугольник АВС (закрашен серым цветом, АВ и ВС -катеты).
Если квадраты отложить в общую часть полуплоскостей с границами АВ и ВС, то сумма числовых значений площадей квадратов, построенных на катетах, равна 4SABC (квадраты совпали). Но и площадь квадрата, построенного на гипотенузе, тоже равна 4SABC
Если же квадраты отложить на сторонах во внешнюю область, то и в этом случае 2+2=4.
Теорема доказана.
Простейшее доказательство
Слайд 19
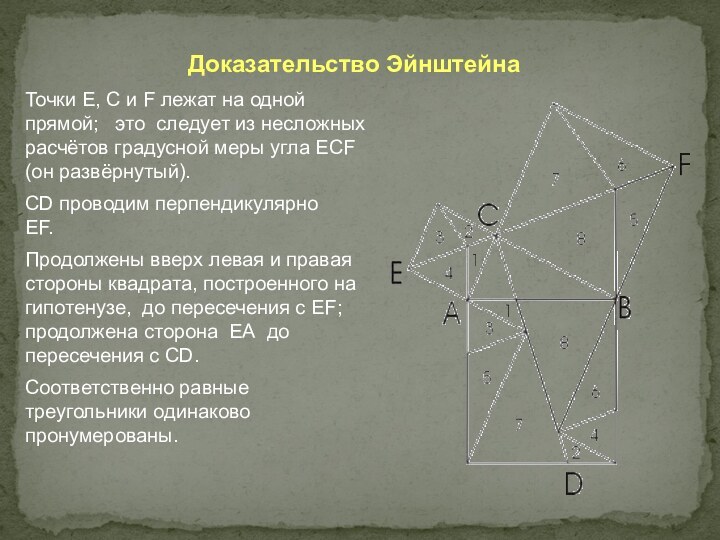
Доказательство Эйнштейна
Точки E, C и F лежат на
одной прямой; это следует из несложных расчётов градусной
меры угла ECF (он развёрнутый).
CD проводим перпендикулярно EF.
Продолжены вверх левая и правая стороны квадрата, построенного на гипотенузе, до пересечения с EF; продолжена сторона ЕА до пересечения с CD.
Соответственно равные треугольники одинаково пронумерованы.
Слайд 20
Доказательство Евклида
В самом деле, треугольники ABD и BFC

равны по двум сторонам и углу между ними: FB = AB, BC = BD, а углы между ними равны как тупые углы со взаимно перпендикулярными сторонами.
SABD = 0,5S BJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=0,5S ABFH
(BF-общее основание, АВ-общая высота). Отсюда, учитывая, что SABD=SFBC, имеем SBJLD=SABFH.
Аналогично, если вы проведёте отрезок АЕ используете равенство треугольников ВСК и АСЕ, то докажете, что SJCEL=SACKG.
Итак, SABFH+SACKG= SBJLD+SJCEL= SBCED, что и требовалось доказать.
Это доказательство было приведено Евклидом в его "Началах". По свидетельству Прокла (Византия), оно придумано самим Евклидом. Доказательство Евклида приведено в предложении 47 первой книги "Начал".
На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник JCEL - квадрату АGКС. Тогда сумма площадей квадратов на катетах будет равна площади квадрата на гипотенузе.
Слайд 21
рис. 2
Древнекитайское доказательство. на древнекитайском чертеже четыре равных

прямоугольных треугольника с катетами а, b и гипотенузой с
уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний — квадрат со стороной с, построенный на гипотенузе (б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (в), то ясно, что образовавшаяся пустота, с одной стороны, равна с2, а с другой — а2+Ь2, т.е. с2=а2+Ь2. Теорема доказана. Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (а), не используются. По-видимому, древнекитайские математики имели другое доказательство. Именно если в квадрате со стороной с два заштрихованных треугольника (б) отрезать и приложить гипотенузами к двум другим гипотенузам (г), то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и b, т.е. с2=а2+Ь2.
Слайд 22
Рис. 4
Древнеиндийское доказательство.
Математики Древней Индии заметили, что
для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского
чертежа. В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика XII в. Бхаскары помещен чертеж (а) с характерным для индийских доказательств словом «смотри!». Как видим, прямоугольные треугольники уложены здесь гипотенузой наружу и квадрат с2 перекладывается в «кресло невесты» а2-b2 (б). Заметим, что частные случаи теоремы Пифагора (например, построение квадрата, площадь которого вдвое больше площади данного квадрата) встречаются в древнеиндийском трактате «Сульва сутра» (VII —V вв. до н.э.).
Слайд 23
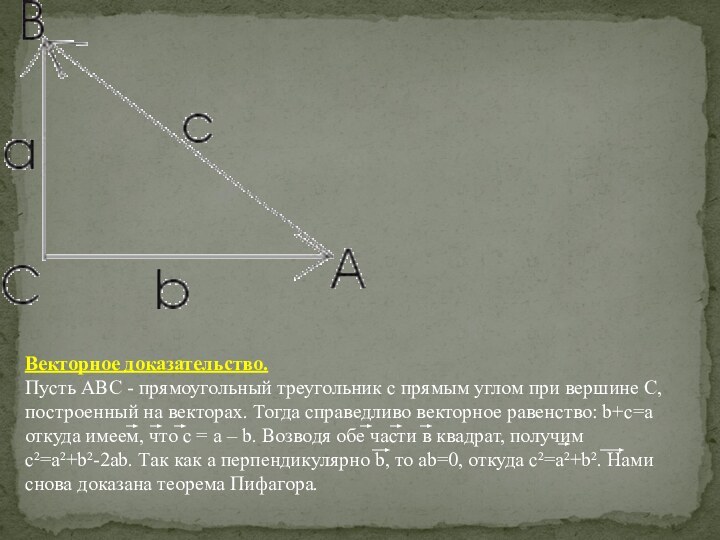
Векторное доказательство.
Пусть АВС - прямоугольный треугольник с прямым
углом при вершине С, построенный на векторах. Тогда справедливо
векторное равенство: b+c=a откуда имеем, что c = a – b. Возводя обе части в квадрат, получим c²=a²+b²-2ab. Так как a перпендикулярно b, то ab=0, откуда c²=a²+b². Нами снова доказана теорема Пифагора.
Слайд 24
Уделом истины не может быть забвенье
Как только мир ее увидит взор
И теорема та, что дал нам Пифагор,
Верна теперь, как в день ее рожденья.
За светлый луч с небес вознес благодаренье Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье
.Быки с тех пор, как только весть услышат , Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Не в силах преградить той истине дорогу.
Они, закрыв глаза, дрожат и еле дышат.
Слайд 25
Область применения.
Теорема Пифагора всегда имела широкое применение при
решении самых разнообразных геометрических задач.
Слайд 26
.«В зданиях романского и готического стиля
верхние части окон расчленяются каменными рёбрами, которые не только
играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его весьма прост: из рисунка легко найти центры шести дуг окружностей, радиусы которых равны.
Слайд 27
А прямой угол при геодезических измерениях отмечают
на местности колышками с помощью верёвки. Если её разметить
углами на местности размером 3, 4 и 5 метров и образовать из верёвки прямоугольный треугольник с соответственными длинами сторон, то он будет прямоугольным. Прямоугольные треугольники с целочисленными длинами сторон называются пифагоровыми треугольниками.
Слайд 28
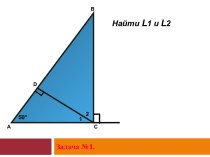
В середине квадратного озера со стороной 10 футов
растет тростник, выходящий из воды на 1 фут. Если
нагнуть тростник, вершина достигнет берега. Какова глубина озера?
Дано: BC = 5 футов, BK = 1 фут.
Найти: AB.
Решение. 1) Пусть AB = x, BC = 5, AC = x + 1.
2) Из ABC по теореме Пифагора имеем
(x + 1)2 = x2 + 52.
x2 +2x+1=x2+25
2x=24
х=12
Ответ: глубина озера 12 футов.
Задача из старинного китайского трактата.
Слайд 29
Задача индийского ученого Бхаскара Акариа, 1114 г.). На берегу
ручья, ширина которого 4 фута, рос тополь. Порыв ветра
сломил его на высоте в 3 фута от земли так, что верхний конец его коснулся другого берега ручья (ствол направлен перпендикулярно течению). Определить высоту тополя.
Решение.
1) AB2 = AC2 + BC2, AB = 5,
2) 5 + 3 = 8 (футов) – высота тополя.
Ответ: высота поля 8 футов
Слайд 31
Первая тайна заключается в таком множестве названий: «теорема
бабочки», «т. невесты», «т. нимфы», « т. 100 быков»,
«бегство убогих», «мост ослов», «ветряная мельница». Думаю, что не найти другой теоремы, которая имела бы столько всевозможных названий!
Слайд 32
Вторая тайна – точно неустановленное количество доказательств знаменитой
теоремы Пифагора Самосского. Именно по этому поводу я решила
провести социологический опрос, который показал, что большинство людей старшего поколения согласны с существованием 250 доказательств, хотя мне из дополнительных источников известно, что существует более 350 доказательств этой теоремы, поэтому она даже попала в Книгу рекордов Гиннеса! Но, конечно же, принципиально различных идей в этих доказательствах используется сравнительно немного.
Слайд 33
Третья тайна – это то, что теорема Пифагора
является сегодня символом математики.
Четвёртая тайна – теорема Пифагора
представляет нам богатейший материал для обобщения – важнейшего вида мыслительной деятельности, основы теоретического мышления, которым в совершенстве владеют многие учёные. Здесь можно добавить, что от теоремы Пифагора можно перейти к другим теоремам.
Слайд 34
Пятая тайна заключается в том, что некоторые исследователи
приписывают Пифагору доказательство, которое Евклид приводил в первой книге
своих «Начал». С другой стороны, Прокл (математик V в.) утверждал, что доказательство в «Началах» принадлежало самому Евклиду. Но всё-таки сегодня способ доказательства Пифагора остаётся неизвестным.
Слайд 35
Шестая тайна – легенды о самом Пифагоре, человеке,
который первым доказал эту теорему. Существует легенда, что когда
Пифагор Самосский доказал свою теорему, он отблагодарил богов, принеся в жертву 100 быков. Также о гипнотических способностях учёного ходили легенды: будто он одним своим взглядом мог менять направление полёта птиц. А ещё рассказывали, что этого удивительного человека одновременно видели в разных городах, между которыми было несколько дней пути. И что ему якобы принадлежало «колесо фортуны», вращая которое, он не только предсказывал будущее, но и вмешивался, если это было необходимо, в ход событий.
Слайд 36
Теорема Пифагора действительно занимает важное место в математике,
с ее помощью можно вывести большинство теорем геометрии и
решить множество не только математических задач.
В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Так, например, на рынке мобильной связи идёт большая конкуренция среди операторов. Чем надёжнее связь, тем больше операторов. При строительстве вышки (антенны) часто приходится решать задачу об определении наибольшей высоты антенны, используя теорему Пифагора Самосского. Это еще раз доказывает значимость данной теоремы.
Прошло уже много лет с того момента, когда эта теорема была впервые открыта и доказана, но она до сих пор продолжает привлекать внимание многих исследователей, учёных, учеников…
Вопрос о количестве доказательств теоремы Пифагора является сегодня довольно актуальным, именно поэтому я решила провести социологический опрос.
Выводы:
Слайд 37
Социологический опрос проводился среди людей старшего поколения с
целью выявить, какое количество доказательств знают не учёные и
не исследователи данного вопроса, а обыкновенные люди. А вот и результаты:
Вопрос 1:
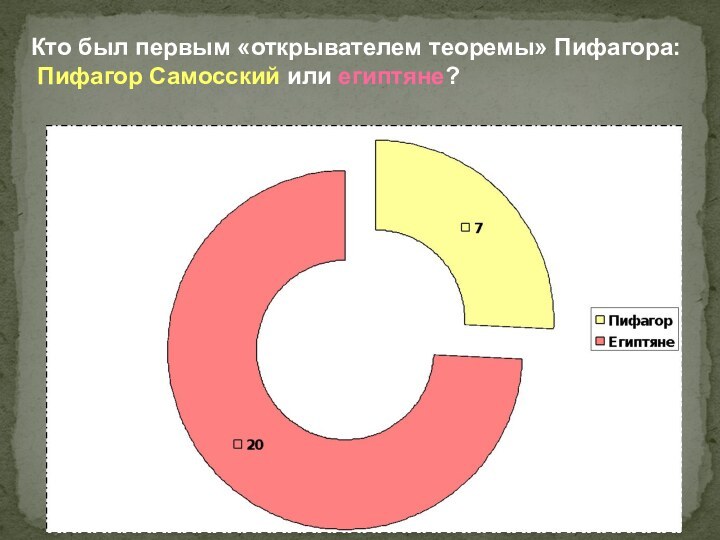
На вопрос: «Кто был первым «открывателем» теоремы Пифагора: Пифагор Самосский или египтяне?» ответили 27 человек, из которых большинство (20 человек) сказали, что первыми «открывателями» знаменитой теоремы были египтяне, остальные утверждали, что именно Пифагор Самосский открыл эту теорему. Эти данные говорят о том, что большинство людей всё-таки знают или догадываются, что Пифагор первым вывел доказательство этой теоремы, которая носит сегодня его имя, но не был 1 её «открывателем».
Социологический опрос
Слайд 38
Кто был первым «открывателем теоремы» Пифагора:
Пифагор Самосский
или египтяне?
Слайд 39
Вопрос 2:
На второй мой
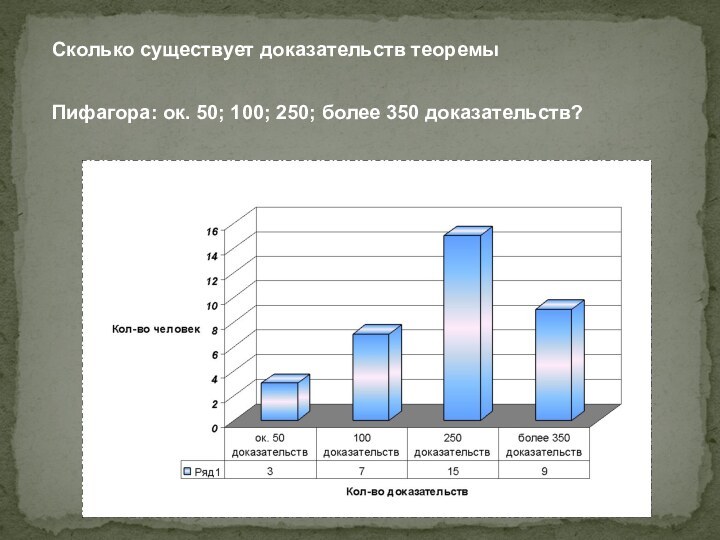
вопрос: «Сколько существует доказательств теоремы Пифагора: ок. 50; 100;
250; более 350 доказательств?» ответили 34 человека. Из них большинство (15 человек) согласны с тем, что существует 250 доказательств теоремы Пифагора, меньшинство (3 человека) сказали, что на сегодняшний день известно всего лишь 50 доказательств, и только 9 человек правильно ответили на мой вопрос, сказав, что сегодня известно более 350 доказательств этой теоремы. Исходя из полученной информации, можно сделать вывод о том, что людям старшего поколения не известно точное количество доказательств теоремы Пифагора Самосского: может быть, их это не интересует, хотя мне кажется, что такая известная теорема должна особенно привлекать внимание населения.
Слайд 40
Сколько существует доказательств теоремы
Пифагора: ок. 50; 100;
250; более 350 доказательств?