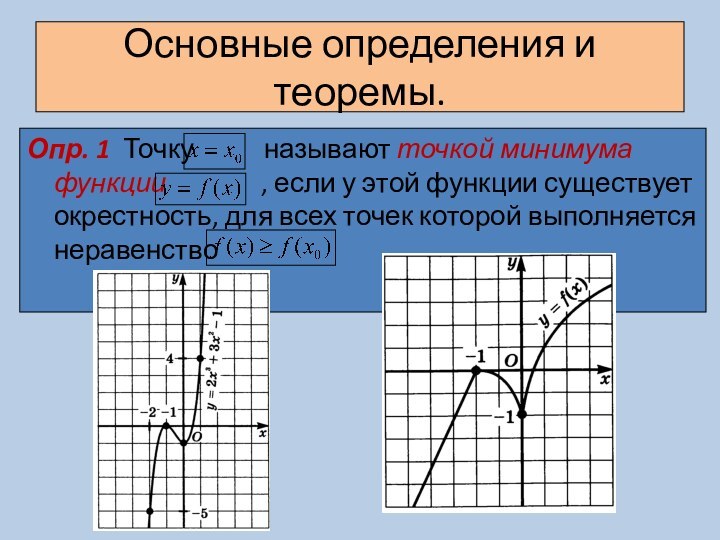
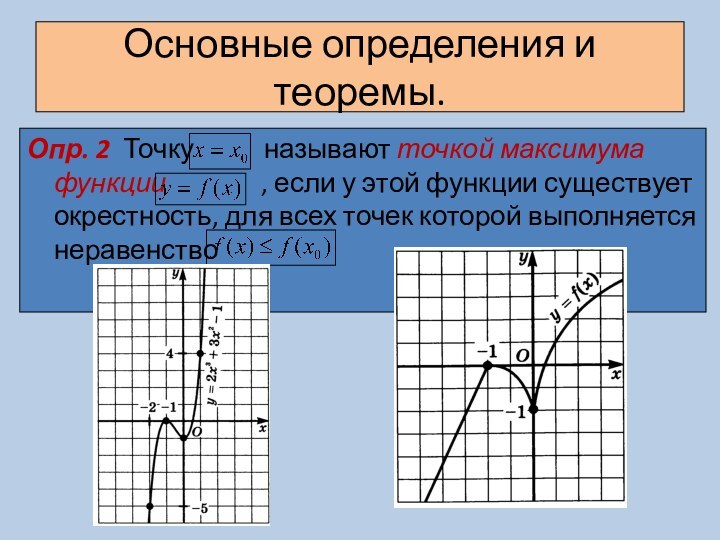
вынести за знак производной.
Производная произведения двух функций равна сумме
двух слагаемых; первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.Производная частного