Презентация на тему Математическая логика

мыслительного процесса.
Логика высказываний- раздел логики, в котором вопрос об

истинности или ложности высказываний рассматривается и решается на основе изучения способа построения высказываний из элементарных с помощью логических связок.

про которое всегда определённо и объективно можно сказать, является

ли оно истинным или ложным.
Высказывания:
1.Абсолютно истинные
2. Абсолютно ложные логические константы
Высказывания обозначаются заглавными латинскими буквами: А, В, С и т. д.

– «3 больше 5»
В=0
Высказывания, которые нельзя разбить на

еще более мелкие, называются простыми, а сконструированные при помощи логических связок – сложными.

Операция отрицания

(операция “не”)

Операция отрицания
делает истинное
высказывание
ложным и ,наоборот,
ложное – истинным.

совершен с применением физического или психического насилия».
Дизъюнкция А∨В –

сложное высказывание, которое ложно тогда и только тогда, когда оба высказывания А и В одновременно ложны.

Дизъюнкция высказываний

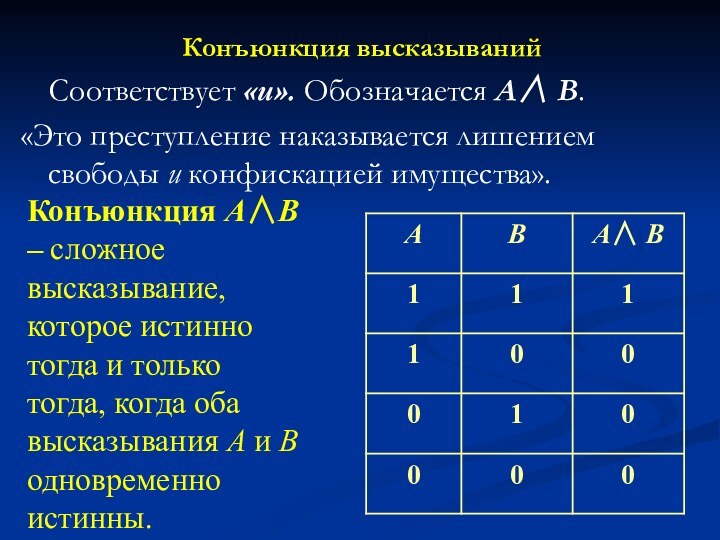
Конъюнкция высказываний
Соответствует «и».

Обозначается А∧ В.
«Это преступление наказывается лишением свободы и конфискацией имущества».

Конъюнкция А∧В – сложное высказывание, которое истинно тогда и только тогда, когда оба высказывания А и В одновременно истинны.

высказывание, которое истинно всегда, кроме случая когда А –

истинно, а В – ложно.

Импликация высказываний

Соответствует объединению двух высказываний с помощью союза «если …, то …» Обозначается А→В.«Если банк отказывает в принятии документов ..., то он обязан незамедлительно проинформировать об этом получателя средств».

равносильно тайному хищению чужого имущества».
Эквивалентность высказываний А и

В (А↔В) – сложное высказывание, которое истинно, когда А и В одновременно либо истинны– истинно, или ложны и ложно во всех других случаях.

Эквивалентность высказываний

Логическая структура правовой нормы:

N= (( J→D ) ^ ( J ^ D ))→ S ,
где J- условие действия нормы права; D- правовое предписание; S- санкция.
Структура норм уголовного права:
(P≡Q)→S
P-конкретный состав преступления; Q-совокупность признаков этого состава; S-санкция, установленная за совершение определённого преступления.

A→B  C ;
(A↔A B )→B ^ A и т.д.

∨

Такие высказывания называются логическими формулами или булевыми функциями , а входящие в них простые высказывания- логическими переменными. Символы ¬ ‚ ^ , , → , ↔ называют логическими связками.

∨

∨

простых высказываний, из которых состоит сложное, и указание соответствующих

значений сложного высказывания.

формулы называются равносильными, если при любых значениях входящих в

них логических переменных эти формулы принимают одинаковые значения.

Равносильность формул обозначается с помощью знака ≡ : A↔B≡(A→B)^(B→A).

«истина», то есть 1, при любых значениях входящих в

неё логических переменных, то такая логическая формула называется тождественно истинная или тавтология.
Факт, что высказывание А является тавтологией, обозначается так |=А.
Сложное высказывание называется тождественно ложным, если оно принимает значение «ложь» при любых значениях входящих в него простых высказываний. То есть, если |=А, то А -тождественно ложно.

, а из высказывания В следует С, то можно

заключить, что из А следует С.
2.Modus ponens.
|=[A^(A→B)]→B.
Если А – истинно и из А следует В, то В также будет истинно.
3. Закон контрапозиции.
|=(A→B)↔(B→A).
Следование из высказывания А высказывания В равносильно тому, что из не В следует не А.