- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Показательная функция
Содержание
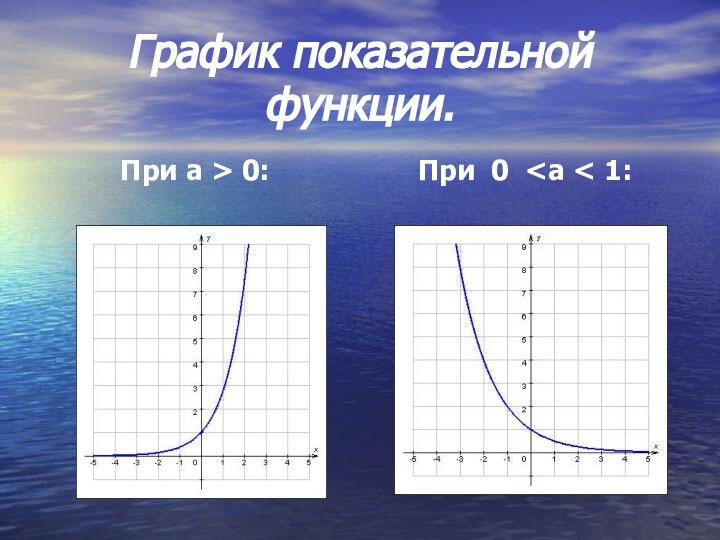
- 2. График показательной функции.При 0 0:
- 3. Свойства показательной функциипри а>0:1.Область определения – множество
- 4. Свойства функцииПри а >1, 0 < а
- 5. Выполни самостоятельно! 1. Постройте график
- 6. Показательные уравненияПоказательными уравнениями называются уравнения вида
- 7. Способы решения показательных уравнений
- 8. Первый способПриведение обеих частей уравнения к одному
- 9. Второй способПутем введения новой переменной приводят уравнение
- 10. Третий способВынесение общего множителя за скобки.Пример:3х ––
- 11. Четвертый способ
- 12. Выполните самостоятельно! Решите
- 13. Показательные неравенстваПоказательными неравенствами называются неравенства вида
- 14. Свойства показательной функцииЕсли а > 0,
- 15. Решение показательных неравенств 22х-4
- 16. Выполни самостоятельно!
- 17. Скачать презентацию
- 18. Похожие презентации















Слайд 3
Свойства показательной функции
при а>0:
1.Область определения – множество действительных
чисел.
2.Область значений – множество положительных действительных чисел.
3.Функция возрастает на
всей числовой прямой. 4.При х = 0, у = 1, график проходит через точку (0; 1)
при 0 < а < 1:
1. Область определения – множество действительных чисел.
2. Область значений – множество положительных действительных чисел.
3. Функция убывает на всей числовой прямой.
4. При х = 0, у = 1, график проходит через точку ( 0 ; 1).
Слайд 4
Свойства функции
При а >1, 0 < а
2. ах : ау = ах-у
3. (а ·в)х = ах · вх 4. (а/в)х = ах/ вх
5. (ах)у = аху
Слайд 5
Выполни самостоятельно!
1. Постройте график функции
у
= 3х2. Сравните числа:
1. 4 ² и 4³
2. (0,3)2 и ( 0,3)-3
3. Вычислите:
1. 21,3 · 2-0,7 · 40,7
2. (27· 64 )1/3
Слайд 6
Показательные уравнения
Показательными уравнениями называются уравнения вида
аf(x) = аq(x), где а – положительное число, отличное
от 1, и уравнения, сводящиеся к этому уравнению.
Слайд 8
Первый способ
Приведение обеих частей уравнения к одному и
тому же основанию.
Пример:
2х = 32,
так как
32= 25, то имеем:2х = 25
х = 5.
Слайд 9
Второй способ
Путем введения новой переменной приводят уравнение к
квадратному.
Пример: 4х + 2х+1 – 24 =
0Решение:
Заметив , что 4х=(22 )х=( 2х)2 и
2х+1 = 2х × 21 , запишем уравнение в виде:
(2х )2 + 2×2х – 24 = 0,
Введем новую переменную 2х = у;
Тогда уравнение примет вид:
У2 + 2у – 24 = 0
Д = в2 – 4 а с = 22 – 4×1×(–24)
= 100> 0, находим у1 = 4, у2 = – 6.
Получаем два уравнения:
2х= 4 и 2х = – 6
22 = 22 корней нет.
х = 2.
Слайд 10
Третий способ
Вынесение общего множителя за скобки.
Пример:
3х –– 3х+3
= –78
3х –3х ×33 = –78
3х ( 1 –33
) = –783х ( – 26) = – 78
33 = – 78 : ( –26)
3х = 3
Х = 1.
Слайд 11
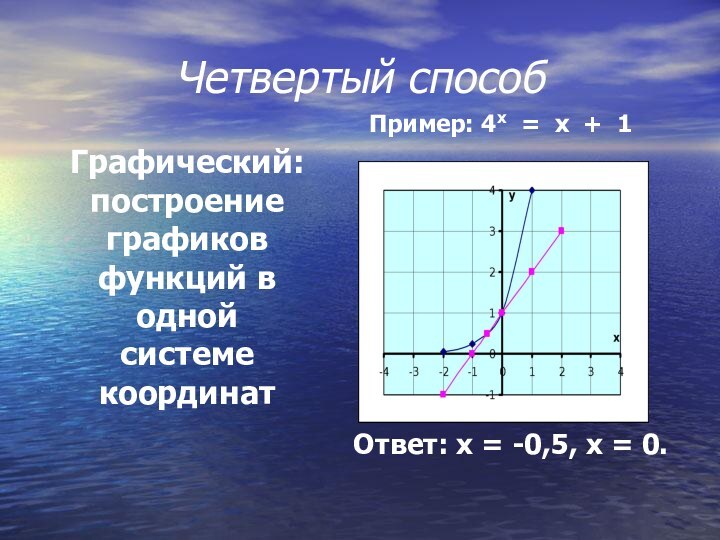
Четвертый способ
Графический:
построение графиков функций в одной системе координат
Пример: 4х = х + 1
Слайд 12
Выполните самостоятельно!
Решите уравнения:
1) (⅓)х+2 = 9
2) 2х-1 = 1
3) 2 ·22х– 3 · 2х - 2 = 0
4) 2х = х + 3
5) 4х+1 + 4х = 320
Слайд 13
Показательные неравенства
Показательными неравенствами называются неравенства вида
аf(x)
> аg(x) , где а – положительное число,
отличное от нуля, и неравенства, сводящиеся к этому виду f(x) > q(x).
Слайд 14
Свойства показательной функции
Если а > 0,
то показательное неравенство
аf (x) >
аg (x) равносильно неравенству того же смысла f(x) > q(x).
Если 0 < а < 1 ,
то показательное неравенство
аf (x) > аg (x) равносильно неравенству противоположного смысла
f(x) < q(x).
Слайд 15
Решение показательных неравенств
22х-4 >
64
22х-4 > 26
2х – 4 > 62х > 10
х > 5
Ответ: х > 5
(0,2)х ≥ 0,04
(0,2)х ≥ (0,2)2
х ≤
Ответ: х ≤ 2
Слайд 16
Выполни самостоятельно!
1. 45-2х ≤ 0,25
2. 0,37+4х > 0,0273. 2х + 2х+2 < 20
4. 112х+3 ≥ 121
5. 54х+2 ≤ 125