значение
7. Наименьшее значение
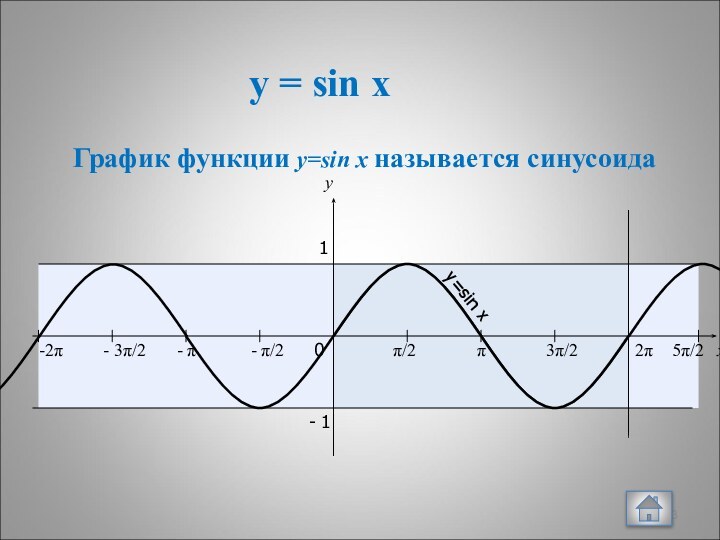
8. Положительные значения
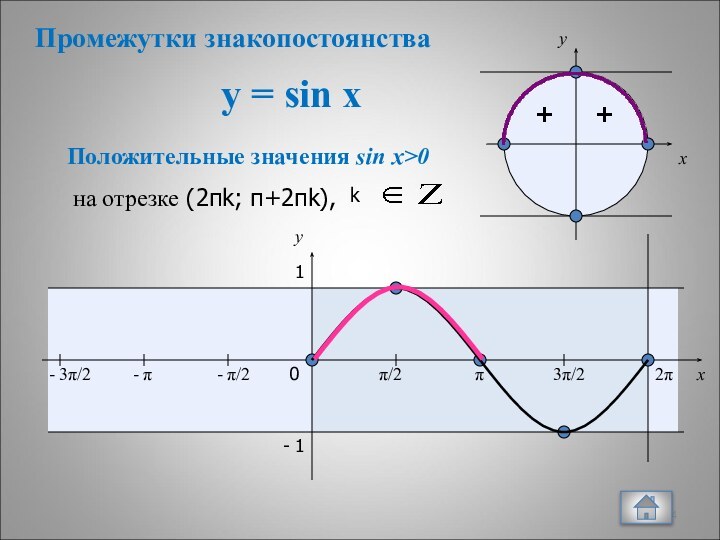
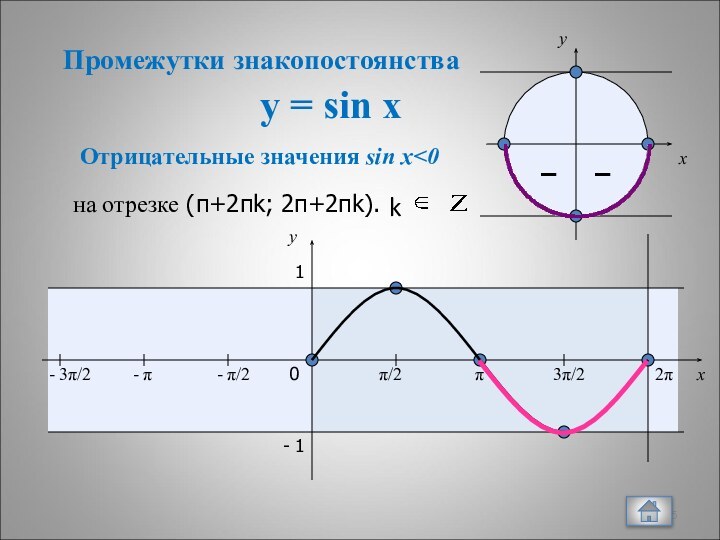
9. Отрицательные значения
10. Возрастание функции
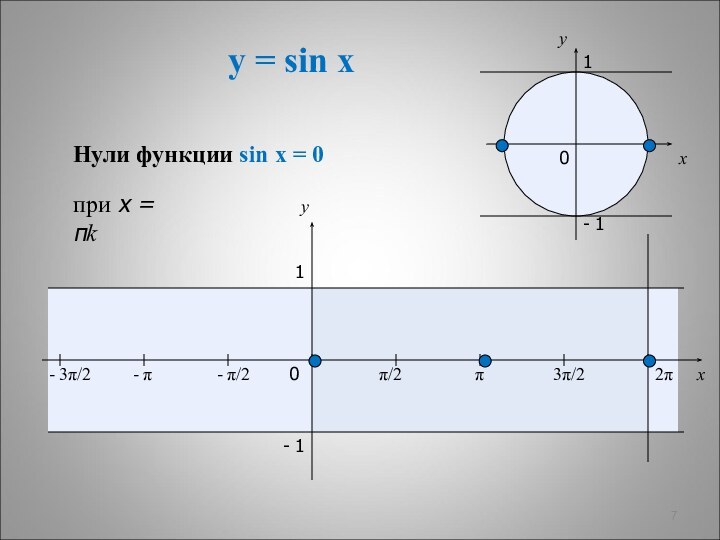
11. Убывание функции
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
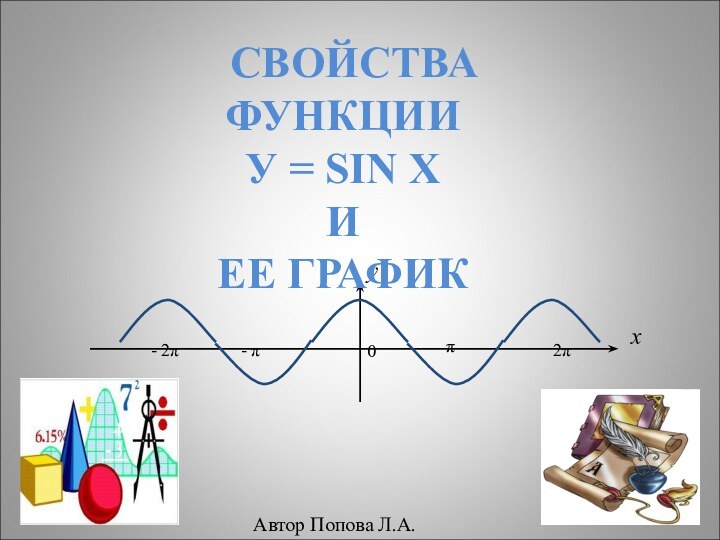


![Свойства функции и ее графики y = sin xxy0π/2π3π/22πxy1- 1- π/2- π- 3π/21- 10 E (y)[ -1; 1]](/img/tmb/12/1161148/a1cdf15a777872a9ff4e228db4635bc9-720x.jpg)

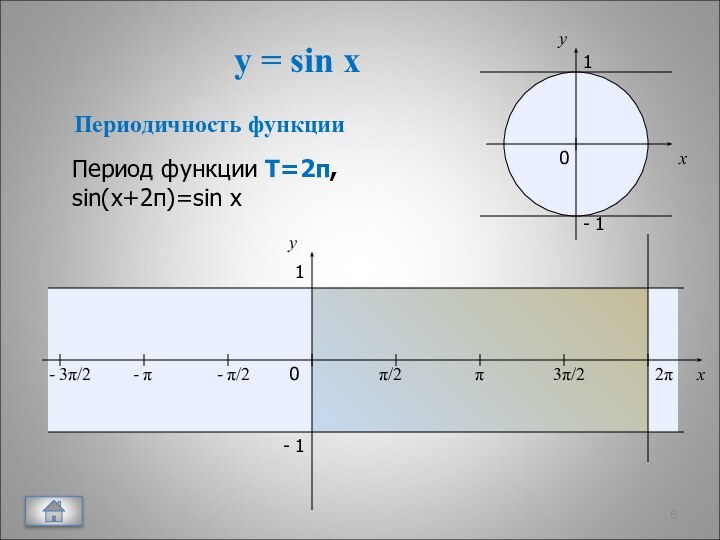




![Свойства функции и ее графики y = sin xxy0π/2π3π/22πxy1- 1 Функция возрастает- π/2- π- 3π/2на отрезке [-π/2+2πk; π/2+2πk]Промежутки возрастания](/img/tmb/12/1161148/aed7807053ac3a8e437e169d85896b4a-720x.jpg)
![Свойства функции и ее графики y = sin xxy0π/2π3π/22πxy1- 1 Функция убывает- π/2- π- 3π/2на отрезке [π/2+2πk; 3π/2+2πk]Промежутки убывания](/img/tmb/12/1161148/e2c837d8f35b8f2111e8bfa4c8d348c8-720x.jpg)








х= π/2
х= 3π/2
k
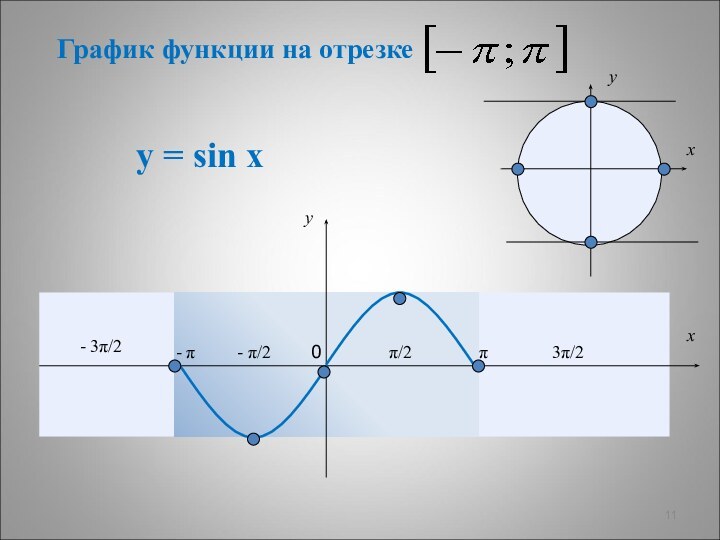
Из графика видно, что на отрезке функция у=sinх убывает.
Ответ: sin 2 > sin 3.
и
Числа sin 1.9 и sin 3 положительны, так как точки Р1,9 и Р3 находятся во 2 четверти. Функция у=sinх во 2 четверти убывает. sin 3 < sin 1.9
Числа sin(-1) и sin(-1.5) отрицательны, так как точка Р(-1) и Р(-1,5) находятся в 4 четверти.
Функция у=sinх во 4 четверти возрастает..
sin(-1.5) < sin(-1.5)
Ответ:
Таким образом, в порядке возрастания эти чила располагаются так:
sin(-1.5); sin(-1); sin 3; sin 1.9.
Ответ; На отрезке функция у=sin х убывает,
а на отрезке функция возрастает.
1)
- Функция возрастает
- Функция убывает
2)
- Функция убывает
- Функция возрастает
3)
- Функция убывает
- Функция возрастает
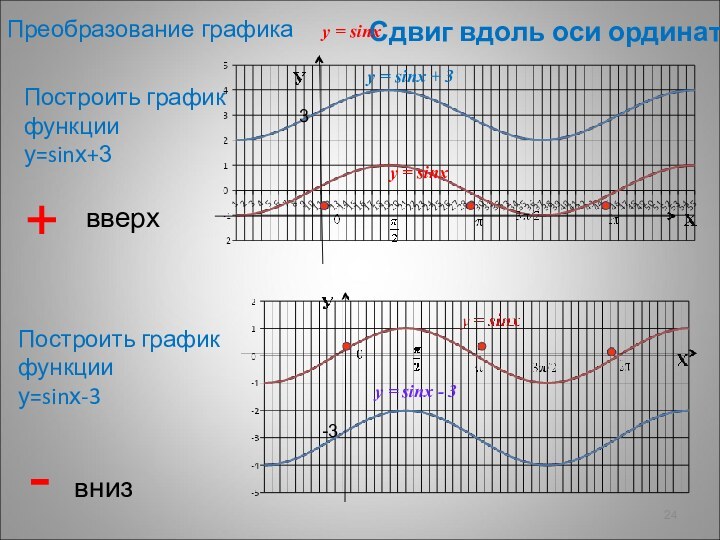
Построить график функции у=sinх-3
+
вверх
-
вниз
y = sinx
y = sinx + 3
y = sinx
y = sinx - 3
3
-3
Преобразование графика
-
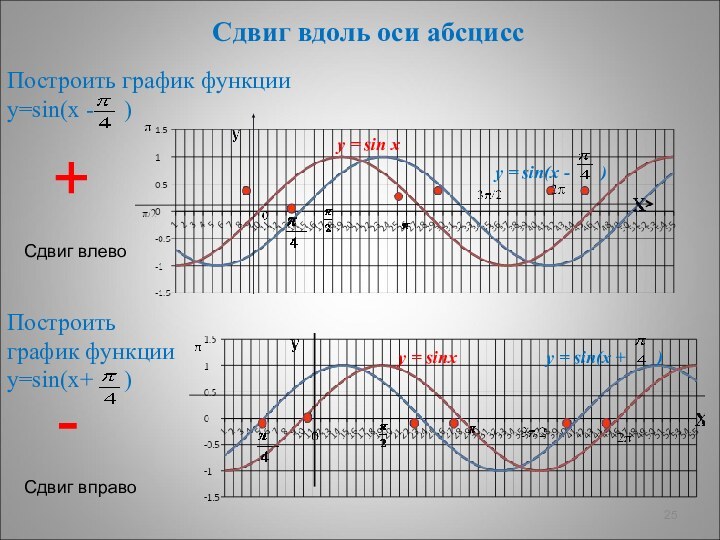
Сдвиг вправо
y = sin x
y = sin(x - )
y = sin(x + )
y = sinx
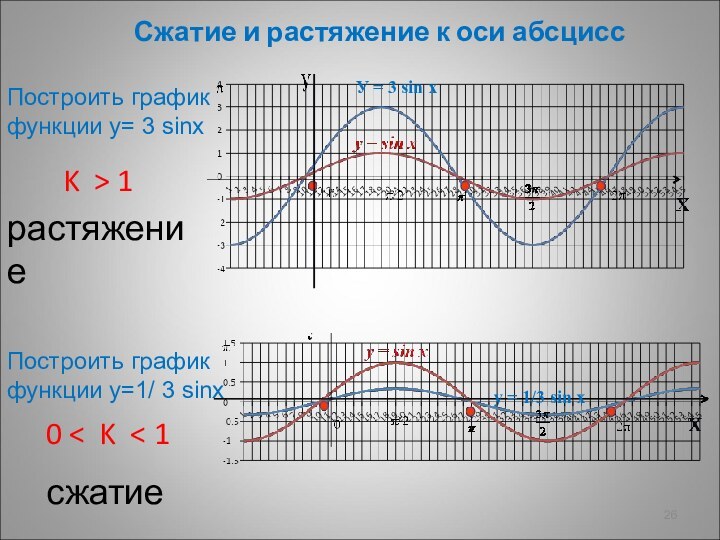
Построить график функции у=1/ 3 sinх
У = 3 sin x
у = 1/3 sin x
сжатие
0 < K < 1
растяжение
У =sin 2х
У = sin