- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Производная показательной, логарифмической и степпеной функци
Содержание
- 2. Содержание.Производная показательной функции. Число .е.Производная логарифмической функции.Степенная функция.
- 3. Производная показательной функции
- 4. Происхождение.Понятие функции является одним из основных понятии
- 5. Происхождение.Уже в 16 - 17 в. в,
- 6. Происхождение.Таким образом, понятие функции носит у него
- 7. Происхождение.Исследование поведения различных систем (технические, экономические, экологические
- 8. Происхождение.В математике XVII в. самым же большим
- 9. Происхождение.Но наряду с интегральными методами складывались и
- 10. Показательная функцияВ практике часто используются функции y=2x,
- 11. Определение: Показательной функцией называется функция
- 12. Свойства показательной функции1) Область определения показательной функции
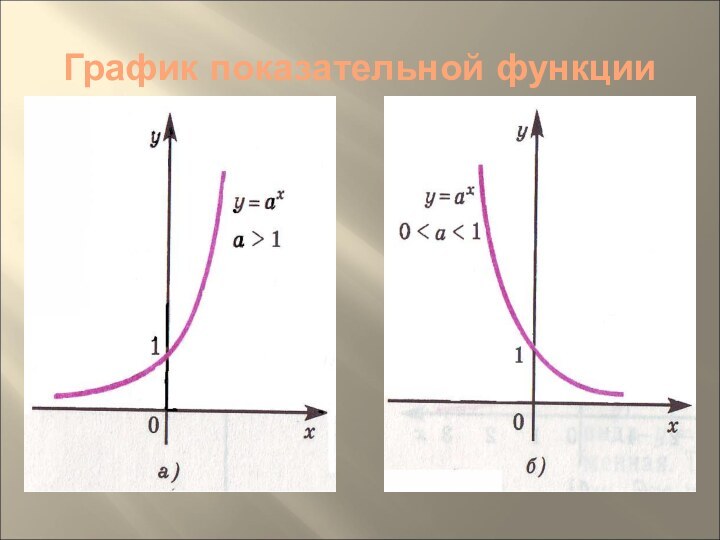
- 13. График показательной функции
- 14. Показательная функция часто используется при описании различных
- 15. Применение производной при решении неравенств Дифференциальное исчисление
- 16. Логарифмическая функция
- 17. Примененя.Широкое применение нашла логарифмическая функция в астрономии:
- 18. Применения.Ещё одно применение логарифмической функции можно найти,
- 19. В математике часто встречается логарифмическая функция y=logax
- 20. Как известно, график обратной функции симметричен графику
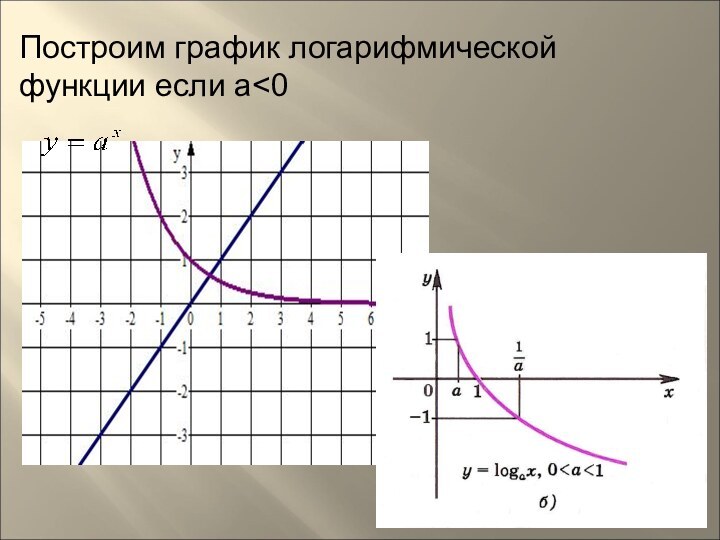
- 21. Построим график логарифмической функции если а
- 22. Таким образом, получаем графики логарифмической функцииРис.1
- 23. Свойства логарифмической функции1) Область определения логарифмической функции
- 24. Степенная функция.
- 25. Вы знакомы с функциями у=х, у=х2, у=хЗ,
- 26. Виды степенной функции1. Показатель р=2n - четное
- 27. Рис. 1
- 28. 2. Показатель р=2n-1 - нечетное натуральное число.
- 29. 3. Показатель р = - 2n, где
- 30. 4. Показатель р = - (2n -
- 31. 5. Показатель р - положительное действительное нецелое
- 32. Рис.5
- 33. Скачать презентацию
- 34. Похожие презентации
Содержание.Производная показательной функции. Число .е.Производная логарифмической функции.Степенная функция.




























Слайд 2
Содержание.
Производная показательной функции. Число .е.
Производная логарифмической функции.
Степенная функция.
Слайд 5
Происхождение.
Уже в 16 - 17 в. в, техника,
промышленность, мореходство поставили перед математикой задачи, которые нельзя было
решить имеющимися методами математики постоянных величин. Нужны были новые математические методы, отличные от методов элементарной математики. Впервые термин "функция" вводит в рассмотрение знаменитый немецкий математик и философ Лейбниц в 1694 г. Однако, этот термин (определения он не дал вообще) он употребляет в узком смысле, понимая под функцией изменение ординаты кривой в зависимости от изменения ее абсциссы.
Слайд 6
Происхождение.
Таким образом, понятие функции носит у него "геометрический
налет". В современных терминах это определение связано с понятием
множества и звучит так:«Функция есть произвольный способ отображения множества А = {а} во множество В = {в}, по которому каждому элементу а[pic]А поставлен в соответствие определенный элемент в[pic]В.
Слайд 7
Происхождение.
Исследование поведения различных систем (технические, экономические, экологические и
др.) часто приводит к анализу и решению уравнений, включающих
как параметры системы, так и скорости их изменения, аналитическим выражением которых являются производные. Такие уравнения, содержащие производные, называются дифференциальными.
Слайд 8
Происхождение.
В математике XVII в. самым же большим достижением
справедливо считается изобретение дифференциального и интегрального исчисления. Сформировалось оно
в ряде сочинений Ньютона и Лейбница и их ближайших учеников. Введение в математику методов анализа бесконечно малых стало началом больших преобразований.
Слайд 9
Происхождение.
Но наряду с интегральными методами складывались и методы
дифференциальные. Вырабатывались элементы будущего дифференциального исчисления при решении задач,
которые в настоящее время и решаются с помощью дифференцирования. В то время такие задачи были трех видов: определение касательных к кривым, нахождение максимумов и минимумов функций, отыскивание условий существования алгебраических уравнений квадратных корней.
Слайд 10
Показательная функция
В практике часто используются функции y=2x, y=10x,
y=(0,1)x и т. д., т. е. функция вида y=ax
где а - заданное число, x -переменная. Такие функции называют показательными.
Слайд 11
Определение:
Показательной функцией называется функция
y=ax
где а - заданное число, a>0 и a≠0.
Слайд 12
Свойства показательной функции
1) Область определения показательной функции -
множество R всех действительных чисел.
2) Множество значений показательной
функции - множество всех положительных чисел R+. 3) Показательная функция у=аХ является возрастающей на множестве всех действительных чисел, если а> 1, и убывающей, если 0<а<1.
Слайд 14 Показательная функция часто используется при описании различных физических
процессов. Так, радиоактивный распад описывается формулой:
M(t)=m0(1/2)t/T
где т (t)
и m0- масса радиоактивного вещества соответственно в момент времени t и в начальный момент времени t = 0, Т – период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое ). С помощью показательной функции выражается давление воздуха в зависимости от высоты подъема, ток самоиндукции в катушке после включения постоянного напряжения, и т.д.
Слайд 15
Применение производной при решении неравенств
Дифференциальное исчисление широко используется
при исследовании функций. С помощью производной можно найти промежутки
монотонности функции, ее экстремальные точки, наибольшие и наименьшие значения.
Слайд 17
Примененя.
Широкое применение нашла логарифмическая функция в астрономии:
Например
по ней изменяется величина блеска звезд, если сравнивать характеристики
блеска отмеченные глазом и с помощью приборов, то можно составить следующий график:По графику видно, что объективные и субъективные характеристики не пропорциональны, а прибор регистрирует возрастание блеска не на одну и ту же величину, а в 2,5 раза. Эта зависимость выражается логарифмической функцией.
Слайд 18
Применения.
Ещё одно применение логарифмической функции можно найти, если
рассматривать логарифмическую спираль.
Спираль, по определению - это плоская
линия, образованная движущейся точкой, которая удаляется по определенному закону от начала луча, равномерно вращающегося вокруг своего начала. Если начало спирали выбрать за полюс полярной системы координат, то математически спираль может быть представлена с помощью некоторого полярного уравнения r = f(j), где r - радиус-вектор спирали, j - угол, откладываемый на полярной оси, f(j) - некоторая монотонно возрастающая или убывающая положительная функция. В случае с логарифмической спиралью точка удаляется по экспоненциальному закону ( , где a - произвольное положительное число).логарифмическая спираль.
Слайд 19
В математике часто встречается логарифмическая функция
y=logax
где а - заданное число, а>0, а ≠ 1.
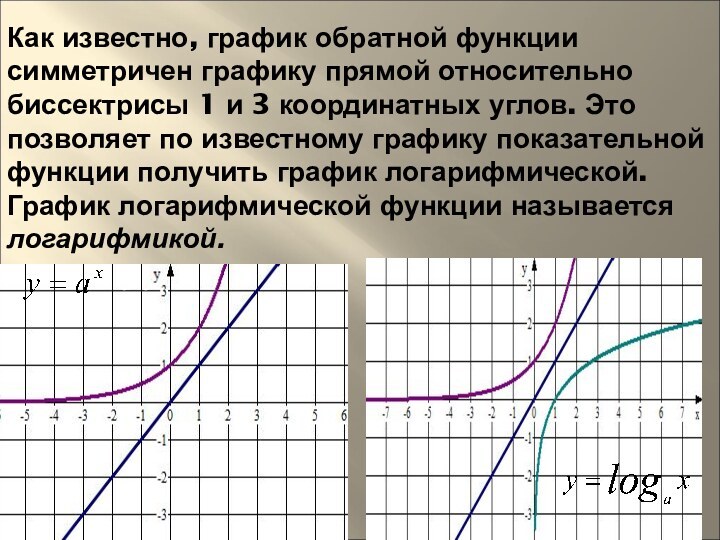
Слайд 20 Как известно, график обратной функции симметричен графику прямой
относительно биссектрисы 1 и 3 координатных углов. Это позволяет
по известному графику показательной функции получить график логарифмической. График логарифмической функции называется логарифмикой.a>0
Слайд 23
Свойства логарифмической функции
1) Область определения логарифмической функции -
множество всех положительных чисел R+.
2) Множество значений логарифмической
функции - множество R всех действительных чисел. 3) Логарифмическая функция y=logax является возрастающей на промежутке х> 0, если а> 1 (рис. 1а), и убывающей, если О < а < 1 (рис. 1б).
4) Если а> 1, то функция y=logax принимает положительные значения при х> 1, отрицательные при 0<х< 1. Если 0<а< 1, то функция y=logax принимает положительные значения при 0<х<1, отрицательные при х>1.
Слайд 25 Вы знакомы с функциями у=х, у=х2, у=хЗ, y=1/х
и т. д. Все эти функции являются частными случаями
степенной функции, т. е. функции у = хР, где р - заданное действительное число.
Слайд 26
Виды степенной функции
1. Показатель р=2n - четное натуральное
число. В этом случае степенная функция у = х2n,
где n - натуральное число, обладает следующими свойствами:- область определения - все действительные числа, т. е. множество R ;
- множество значений - неотрицательные числа, т. е. y≥ 0;
функция у=х2n четная, так как (-х)2n = х2n;
- функция является убывающей на промежутке x≥O и возрастающей на промежутке x≤ O.
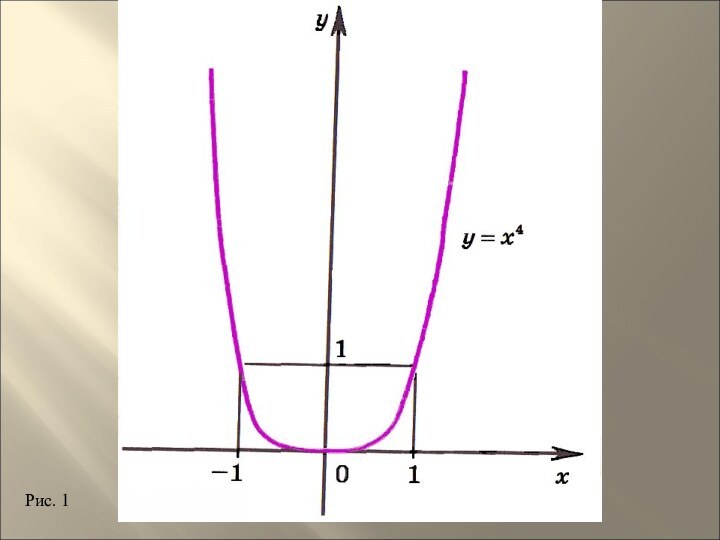
График функции у = хР имеет такой же вид, как, например, график функции у = х4 (рис. 1).
Слайд 28
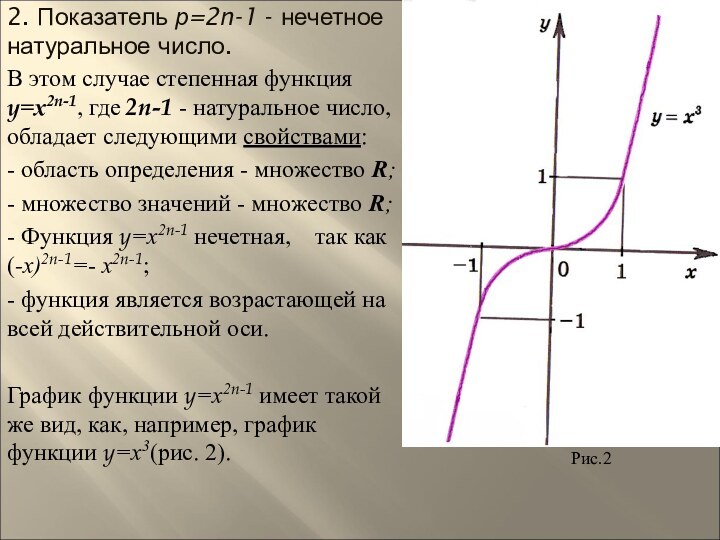
2. Показатель р=2n-1 - нечетное натуральное число.
В
этом случае степенная функция y=х2n-1, где 2n-1 - натуральное
число, обладает следующими свойствами:- область определения - множество R;
- множество значений - множество R;
- Функция y=х2n-1 нечетная, так как (-х)2n-1=- х2n-1;
- функция является возрастающей на всей действительной оси.
График функции y=х2n-1 имеет такой же вид, как, например, график функции y=х3(рис. 2).
Рис.2
Слайд 29 3. Показатель р = - 2n, где n
- натуральное число.
В этом случае степенная функция y=х2n
обладает следующими свойствами: - область определения - множество R, кроме х= 0;
- множество значений - положительные числа у>0;
- Функция y=х2n- четная, так как (-х)2n =х2n;
функция является возрастающей на промежутке х<0 и убывающей на промежутке х>0.
График функции y=х2nимеет такой же вид, как, например, график функции y=х-2(рис.3).
Рис.3
Слайд 30 4. Показатель р = - (2n - 1),
где n - натуральное число.
В этом случае степенная
функция y=х-(2n-1) обладает следующими свойствами: - область определения - множество R, кроме х=0;
- множество значений - множество R, кроме у=0;
- функция нечетная, так как (-х)-(2n-1) = х-(2n-1);
- функция является убывающей на промежутках х<0 и х>0.
График функции y=х-(2n-1) имеет такой же вид, как, например, график функции y=х-3 (рис. 4).
Рис.4
Слайд 31 5. Показатель р - положительное действительное нецелое число.
В этом случае функция у=хР обладает следующими свойствами:
область
определения - неотрицательные числа х; множество значений - неотрицательные числа у;
функция является возрастающей на промежутке (x; ∞).
График функции у=хР, где р - положительное нецелое число, имеет такой же вид, как, например, график функции у=х (при 0<р< 1) или как, например, график функции y=x (при p>1) (рис.5 a, б)





























