- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Разложение многочлена на множители способом группировки
Содержание
- 2. Содержание1) Вынесение общего множителя за скобки2) Способ группировки3)Маленькие исторические факты !!!К содержанию
- 3. Вынесение общего множителя
- 4. Алгоритм нахождения общего множителя нескольких одночленовНайти наибольший
- 5. Пример Разложить на множители: x4y3
- 6. Способ группировки Бывает, что члены
- 7. 1. Сгруппировать его члены так, чтобы
- 8. Для уяснения сути способа группировки рассмотрим следующий пример: разложить на множители многочлен Xy–6+3x–2y
- 9. xy-6+3x-2y==(xy-6)+(3x-2y).Пример не корректный !!!Попробуйте применить другой способ !!!Первый способ группировки:
- 10. Второй способ группировкиxy-6+3x-2y=(xy+3x)+(-6-2y)= =x(y+3)-2(y+3)==(y+3)(x-2).
- 11. xy-6+3y-2y=(xy-2y)+(-6+3x)= =y(x-2)+3(x-2)==(x-2)(y+3). Третий способ группировки:
- 12. Разложение многочлена на множители с помощью комбинации
- 13. xy-6+3y-2y=(x-2)(y+3).К содержаниюВы уже поняли , что не
- 14. А давайте Повторим !!!!
- 16. Завершите утверждение. Представление многочлена в виде произведения одночлена и многочлена называется
- 17. 2. Завершить утверждение. Представление многочлена в виде произведения одночлена и многочлена называется вынесением общего множителя за скобки.
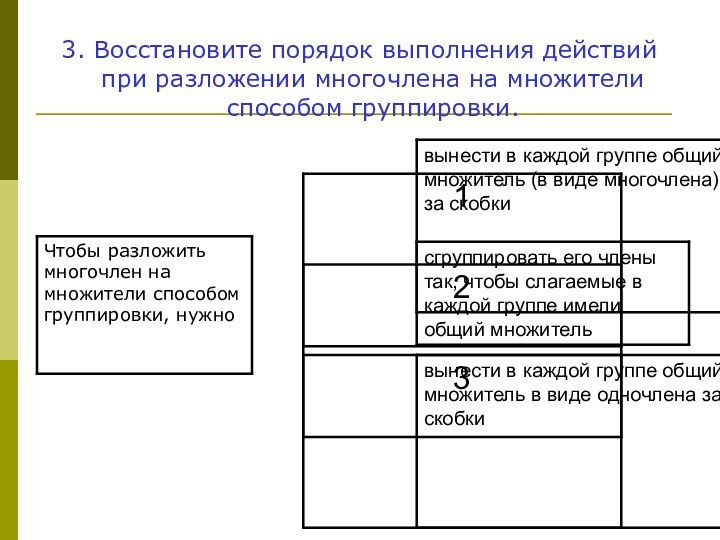
- 18. 3. Восстановите порядок выполнения действий при разложении многочлена на множители способом группировки.
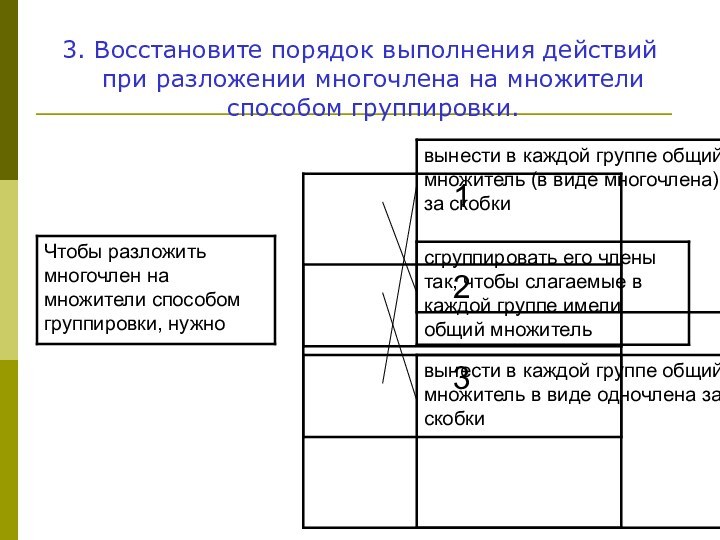
- 19. 3. Восстановите порядок выполнения действий при разложении многочлена на множители способом группировки.
- 20. ИСТОРИЧЕСКИЕ ФАКТЫ !!!Великие математики иУченые !!!
- 21. Известный математик по имени Эйлер (1707 -
- 22. Скачать презентацию
- 23. Похожие презентации
Содержание1) Вынесение общего множителя за скобки2) Способ группировки3)Маленькие исторические факты !!!К содержанию



















Слайд 2
Содержание
1) Вынесение общего множителя за скобки
2) Способ группировки
3)Маленькие
исторические факты !!!
Слайд 3 Вынесение общего множителя за скобки Из каждого слагаемого, входящего
в многочлен, выносится некоторый одночлен, входящий в качестве множителя
во все слагаемые. Таким общим множителем может быть не только одночлен, но и многочлен.
Слайд 4
Алгоритм нахождения общего множителя нескольких одночленов
Найти наибольший общий
делитель коэффициентов всех одночленов, входящих в многочлен, - он
и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.
Слайд 5
Пример
Разложить на множители:
x4y3 - 2x3y2 + 5x2.
Воспользуемся сформулированным
алгоритмом.
Наибольший общий делитель коэффициентов
–1, -2 и 5 равен 1.
Переменная x входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x2.
Переменная y входит не во все члены многочлена; значит, ее нельзя вынести за скобки.
Вывод: за скобки можно вынести x2. Правда, в данном случае целесообразнее вынести -x2. Получим:
-x4y3-2x3y2+5x2=-x2(x2y3+2xy2-5).
К содержанию
Слайд 6
Способ
группировки
Бывает, что члены многочлена не имеют общего
множителя, но после заключения нескольких членов в скобки (на
основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.
Слайд 7
1. Сгруппировать его члены так, чтобы слагаемые
в каждой группе имели общий множитель
2. Вынести в каждой
группе общий множитель в виде одночлена за скобки3. Вынести в каждой группе общий множитель (в виде многочлена) за скобки.
Алгоритм разложения многочлена на множители способом группировки:





























