Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Графическое решение квадратных уравнений

Содержание

Немного историиЕще в древнем Вавилоне могли решить некоторые виды квадратных уравнений.Диофант Александрийский, Аль- Хорезми .Евклид Омар Хайям Решали
Графическое решениеКвадратных уравнений.Выполнила: Темникова А.Е.Педагог математики Немного историиЕще в древнем Вавилоне могли решить некоторые виды квадратных уравнений.Диофант Для графического решения квадратного уравнения представьте его в одном из видов: Алгоритм графического решения квадратных уравненийВвести функцию f(x), равную левой части и g(x) Способы графического решения квадратного уравненияах² + bх + с = 0 Способ «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу Графическое решение квадратного уравненияИллюстрация на одном примере Алгоритм решения квадратного уравнения графическим способомСпособ 1Построить график функции y=ax2+bx+cНайти точки пересечения графика с осью абсцисс Решить уравнение 1 способКорнями уравнения являются абсциссы точек пересечения графика с осью Алгоритм построения параболынайти координаты вершины; провести ось параболы;отметить на оси абсцисс две Пусть f(x)= x2 – 2x -3 и g(x) =0а = 1>0, ветви Графический способ решения квадратных уравнений Квадратное уравнение имеет два равных корня Алгоритм решения квадратного уравнения графическим способомСпособ 2(а)Построить графики функции y=ax2 и x2 – 2x – 3 =0 Представим в виде x2 = 2 способПреобразуем уравнение к виду Построим в одной системе координат графики функций 4 x2 – 4x + Алгоритм решения квадратного уравнения графическим способомСпособ 2 (b)Преобразовать уравнение к виду ax2+с x2 – 2x – 3 =0 x2 – 4x + 5 =0 Алгоритм решения квадратного уравнения графическим способомСпособ 2(в)Построить графики функции y=ax2 + bx x2 – 2x – 3 =0 Представим в виде x2 – Алгоритм решения квадратного уравнения графическим способомСпособ 3 (выделение полного квадрата)Преобразовать уравнение к Выделение квадрата двучлена. x2 – 2x + 1 = 3 x2 – 2x – 3 =0 Представим в виде (x –1)2=4Пусть Решите графически уравнениеГруппа АГруппа СГруппа В х² + 2х – 8= Сколько нам открытий чудных готовит просвещения дух? Решить графически уравнение Как решить уравнение?Построить график квадратичной функции и абсциссы точек пересечения параболы с Решить графически уравнение Построить график функции Построить график функции Корни уравнения: абсциссы точек пересечения графиков функций Построить график функцииКорни уравнения:точки пересечения параболы с осью ОХ Решить графически уравнениеКорни уравнения:точки пересечения параболы и прямой Решить графически уравнениеКорни уравнения:точки пересечения параболы и прямой Итог Познакомились: с графическим методом решения квадратных уравнений;с различными способами графического решения Заключительное слово учителя:«Чем больше и глубже вам удастся усвоить азы математики и Желаю удачи !
Слайды презентации

Слайд 2 Немного истории
Еще в древнем Вавилоне могли решить

Немного историиЕще в древнем Вавилоне могли решить некоторые виды квадратных

некоторые виды квадратных уравнений.
Диофант Александрийский,

Аль- Хорезми


.


Евклид Омар Хайям


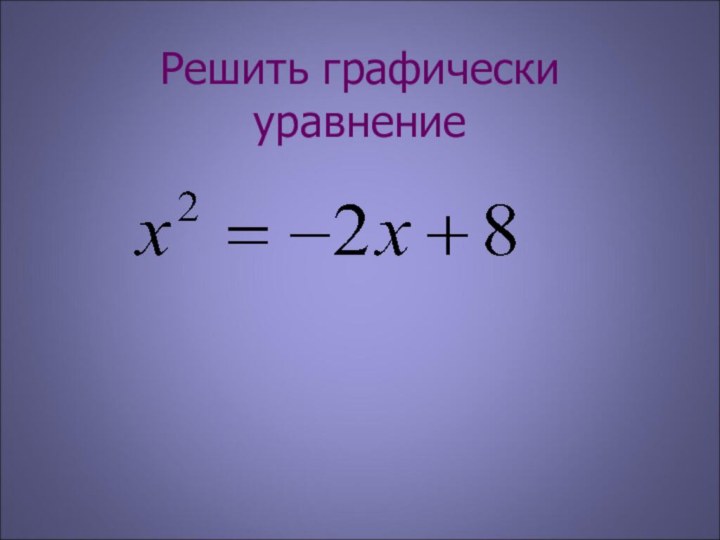
Решали уравнения
геометрическими и
графическими способами





Слайд 3 Для графического решения квадратного уравнения представьте его

Для графического решения квадратного уравнения представьте его в одном из

в одном из видов:
ax2 + bx +c =

0
ax2 = -bx – c
ax2 + c = - bx
a(x + b/2a)2 = ( 4ac - b2 )/4a

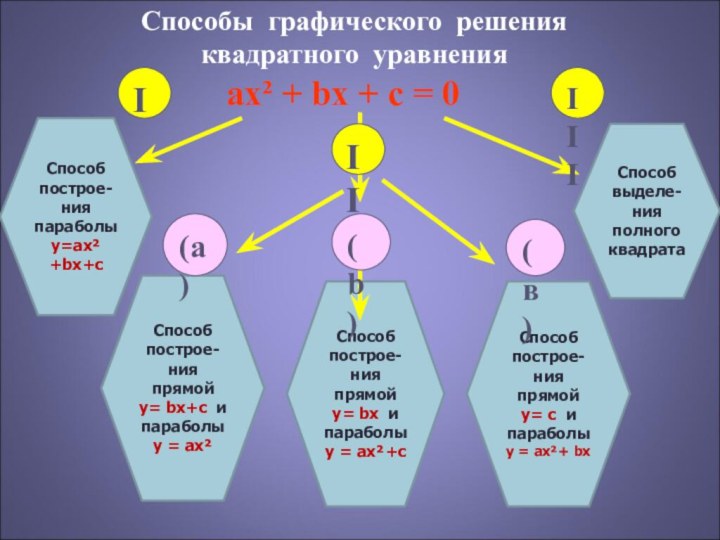
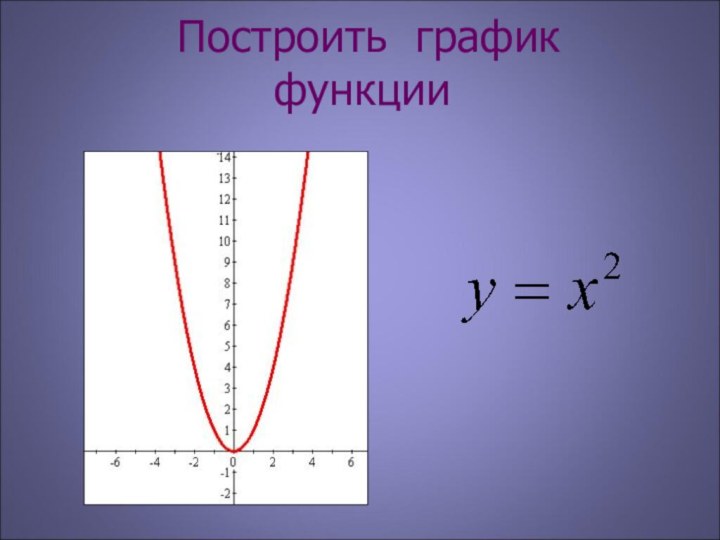
Квадратное уравнение имеет вид ax2 + bx + c = 0

Слайд 4 Алгоритм графического решения квадратных уравнений
Ввести функцию f(x), равную

Алгоритм графического решения квадратных уравненийВвести функцию f(x), равную левой части и

левой части и g(x) , равную правой части
Построить

графики функций y=f(x) и y=g(x) на одной координатной плоскости
Отметить точки пересечения графиков
Найти абсциссы точек пересечения, сформировать ответ

Слайд 5 Способы графического решения квадратного уравнения
ах² + bх +

Способы графического решения квадратного уравненияах² + bх + с = 0

с = 0






Способ поcтрое-
ния параболы y=ах² +bx+c


Способ поcтрое-
ния прямой
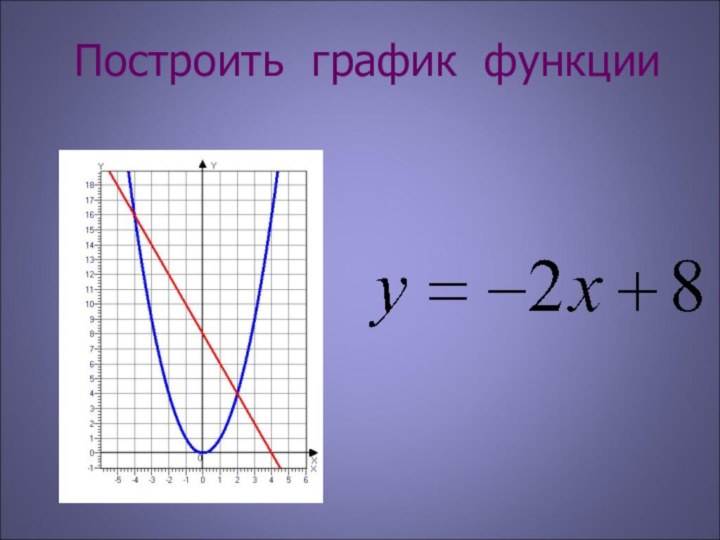
у= bx+c и параболы у = ах²

Способ поcтрое-
ния прямой
у= bx и параболы у = ах²+с

Способ выделе-ния полного квадрата

I

II

III

(a)

(b)

Способ поcтрое-
ния прямой
у= с и параболы у = ах²+ bx

(в)

Слайд 6 «Человеку, изучающему алгебру, часто полезнее решить одну

«Человеку, изучающему алгебру, часто полезнее решить одну и ту же

и ту же задачу различными способами, чем решать три-четыре

различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт». У. У. Сойер.

Слайд 7 Графическое решение квадратного уравнения

Иллюстрация на одном примере

Графическое решение квадратного уравненияИллюстрация на одном примере

Слайд 8 Алгоритм решения квадратного уравнения графическим способом
Способ 1
Построить график

Алгоритм решения квадратного уравнения графическим способомСпособ 1Построить график функции y=ax2+bx+cНайти точки пересечения графика с осью абсцисс

функции y=ax2+bx+c
Найти точки пересечения графика с осью абсцисс

Слайд 9 Решить уравнение
1 способ







Корнями уравнения являются
абсциссы точек

Решить уравнение 1 способКорнями уравнения являются абсциссы точек пересечения графика с

пересечения графика с осью х, т.е. где у=0.
Значит, корни

уравнения -1 и 3. Проверка устно. Ответ: -1; 3.

-1

1

-1

3

х

3

о

у

Слайд 10 Алгоритм построения параболы
найти координаты вершины; провести ось параболы;
отметить

Алгоритм построения параболынайти координаты вершины; провести ось параболы;отметить на оси абсцисс

на оси абсцисс две точки, симметричные относительно оси параболы;

найти значения функции в этих точках;
провести параболу через полученные точки.

Слайд 11 Пусть f(x)= x2 – 2x -3 и g(x)

Пусть f(x)= x2 – 2x -3 и g(x) =0а = 1>0,

=0
а = 1>0, ветви вверх
Координаты вершины x۪۪ ο =-b/2a;

x۪۪ ο =1 .
y ο = 1² - 2 – 3 = -4; y ο = -4; ( 1; -4)
Найти точки абсциссы которых симметричны относительно х=1
Построить по таблице график y=x2 -2x -3

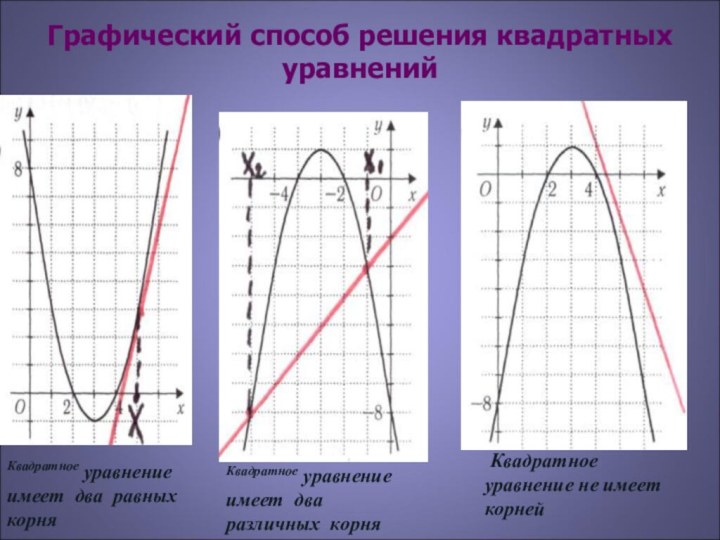
Примеры графического решения квадратных уравнений



3

-1


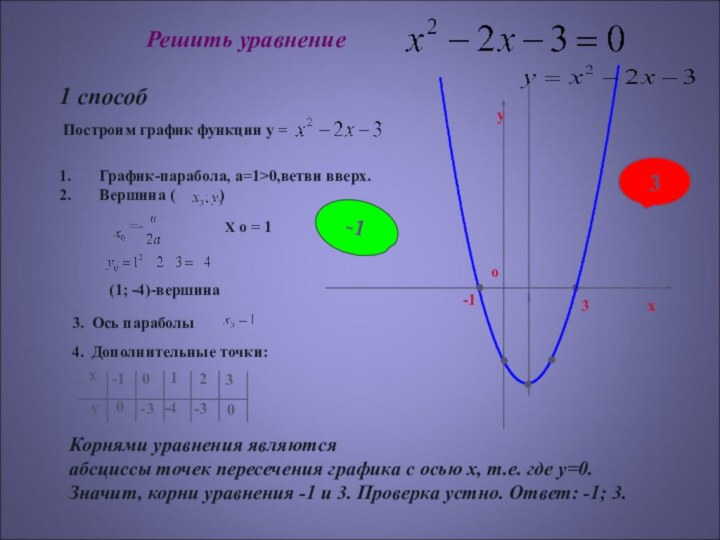
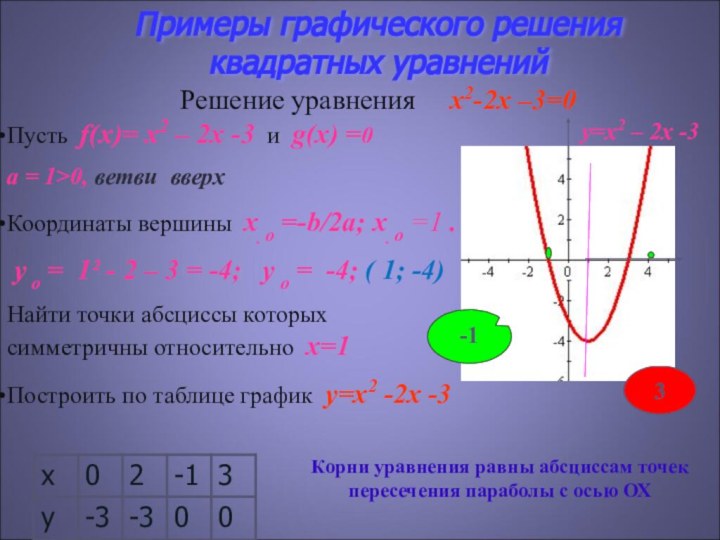
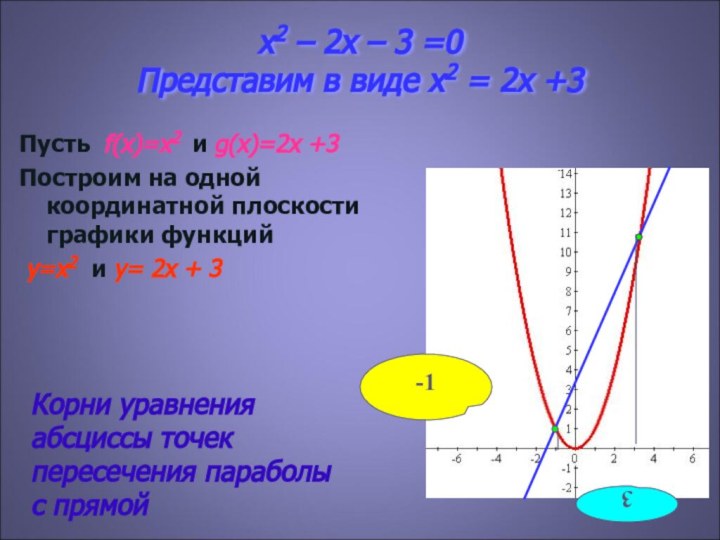
Решение уравнения x2-2x –3=0

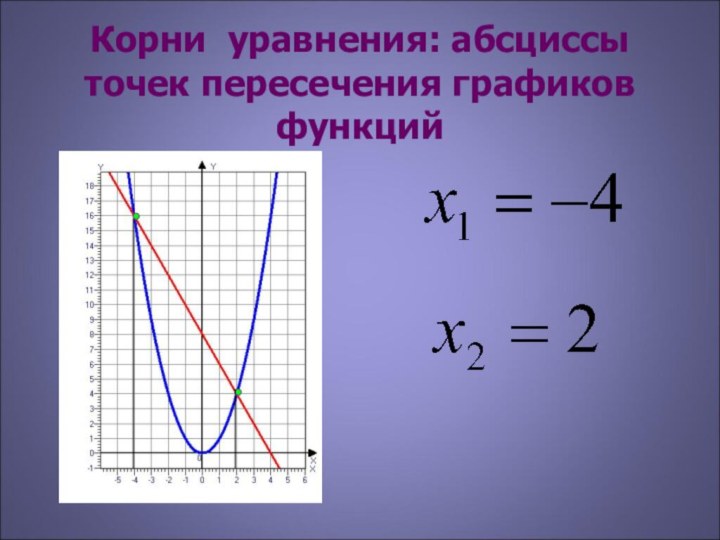
Корни уравнения равны абсциссам точек пересечения параболы с осью ОХ

у=x2 – 2x -3

Слайд 12 Графический способ решения квадратных уравнений

Квадратное уравнение имеет

Графический способ решения квадратных уравнений Квадратное уравнение имеет два равных корня

два равных корня
Квадратное уравнение не имеет корней
Квадратное

уравнение имеет два различных корня

Слайд 13 Алгоритм решения квадратного уравнения графическим способом
Способ 2(а)
Построить графики

Алгоритм решения квадратного уравнения графическим способомСпособ 2(а)Построить графики функции y=ax2 и

функции y=ax2 и у = bx+ с
Найти абсциссы

точек пересечения графиков.

Слайд 14 x2 – 2x – 3 =0 Представим в

x2 – 2x – 3 =0 Представим в виде x2 =

виде x2 = 2x +3
Пусть f(x)=x2 и g(x)=2x +3
Построим

на одной координатной плоскости графики функций
y=x2 и y= 2x + 3



3

-1

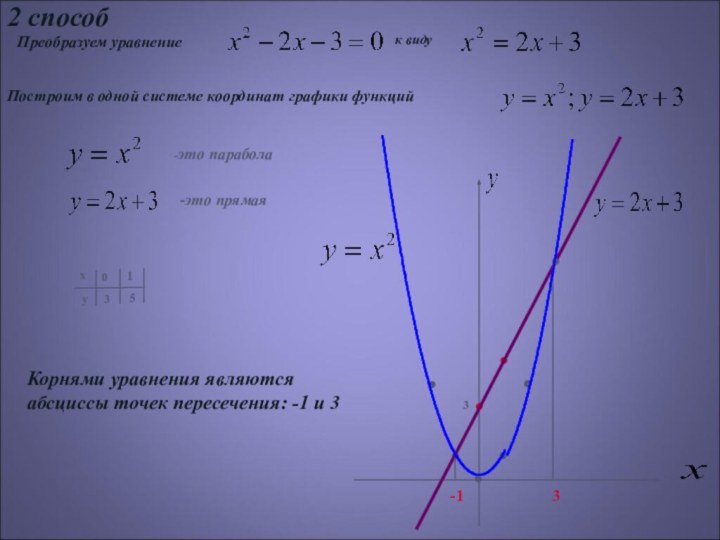
Корни уравнения абсциссы точек пересечения параболы с прямой

Слайд 15
2 способ
Преобразуем уравнение
к виду
Построим в одной

2 способПреобразуем уравнение к виду Построим в одной системе координат графики

системе координат графики функций
-это парабола
-это прямая
х
у
0
1
3
5










3

-1
3
Корнями уравнения являются


абсциссы точек пересечения: -1 и 3

Корнями уравнения являются
абсциссы точек пересечения: -1 и 3

Слайд 16 4

4 x2 – 4x + 1 =0

x2 – 4x + 1 =0 Представим в виде

4x2 = 4x -1


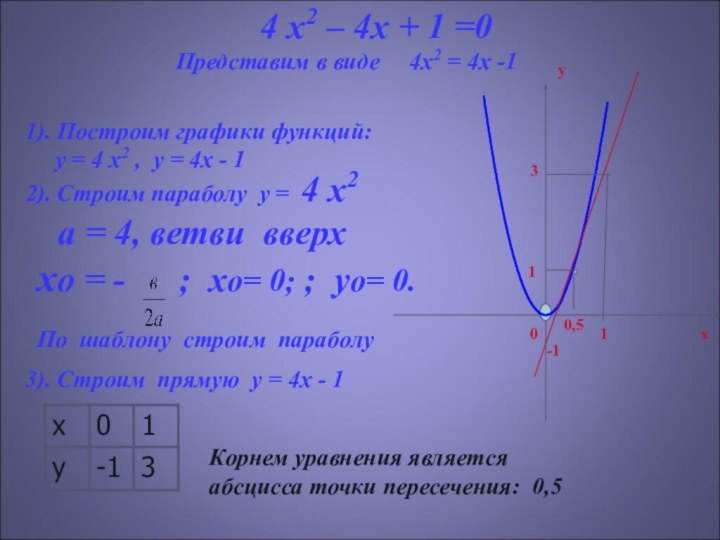
1). Построим графики функций:
у = 4 x2 , у = 4x - 1

2). Строим параболу у = 4 x2
а = 4, ветви вверх
хο = - ; хο= 0; ; уο= 0.

По шаблону строим параболу
3). Строим прямую у = 4x - 1


-1

0

1

3

1

0,5

Корнем уравнения является
абсцисса точки пересечения: 0,5

-1

-1


у

х

Слайд 17 Алгоритм решения квадратного уравнения графическим способом
Способ 2 (b)
Преобразовать

Алгоритм решения квадратного уравнения графическим способомСпособ 2 (b)Преобразовать уравнение к виду

уравнение к виду
ax2+с = bx
Построить:
параболу y

= ax2+с и прямую y = bx
Найти абсциссы точек пересечения
графиков функции.

Слайд 18 x2 – 2x – 3 =0

x2 – 2x – 3 =0 Представим

Представим в виде x2

–3 = 2x

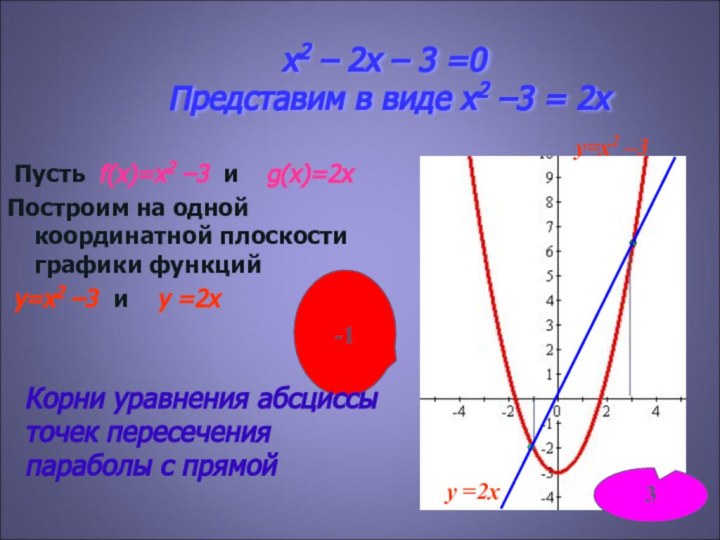
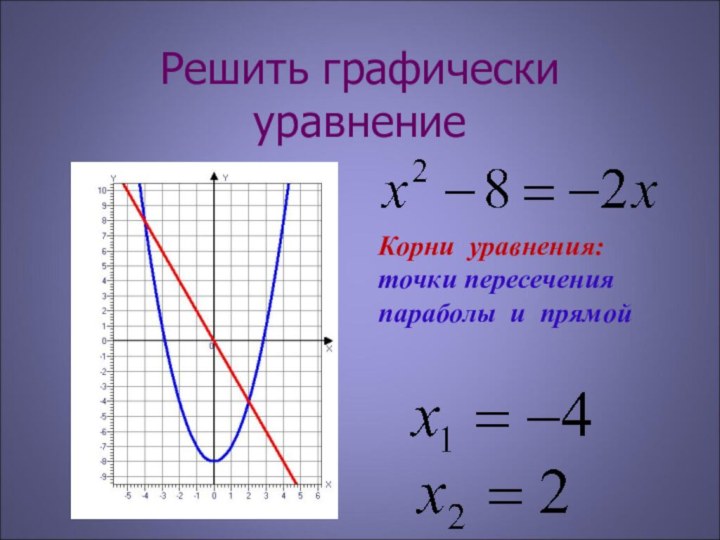
Пусть f(x)=x2 –3 и g(x)=2x
Построим на одной координатной плоскости графики функций
y=x2 –3 и y =2x




-1

3

Корни уравнения абсциссы точек пересечения параболы с прямой

y=x2 –3

y =2x

Слайд 19 x2 – 4x + 5 =0

x2 – 4x + 5 =0 Представим

Представим в виде x2

+5 = 4x

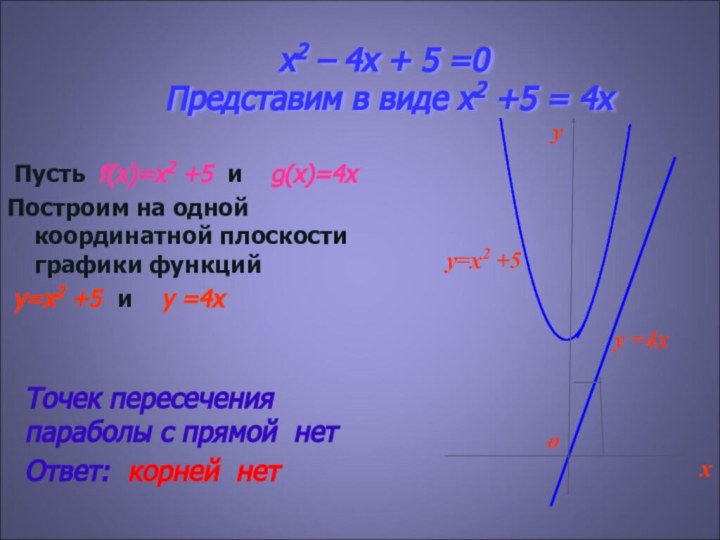
Пусть f(x)=x2 +5 и g(x)=4x
Построим на одной координатной плоскости графики функций
y=x2 +5 и y =4x

Точек пересечения параболы с прямой нет
Ответ: корней нет

y=x2 +5

y =4x

y

x

о

Слайд 20 Алгоритм решения квадратного уравнения графическим способом
Способ 2(в)
Построить графики

Алгоритм решения квадратного уравнения графическим способомСпособ 2(в)Построить графики функции y=ax2 +

функции
y=ax2 + bx и у = с
Найти

абсциссы точек пересечения графиков.

Слайд 21 x2 – 2x – 3 =0 Представим в

x2 – 2x – 3 =0 Представим в виде x2 –

виде x2 – 2x = 3
Пусть f(x)= х²

- 2х и g(x)=3
Построим на одной координатной плоскости графики функций
y= х² - 2х и y=3



-1


3

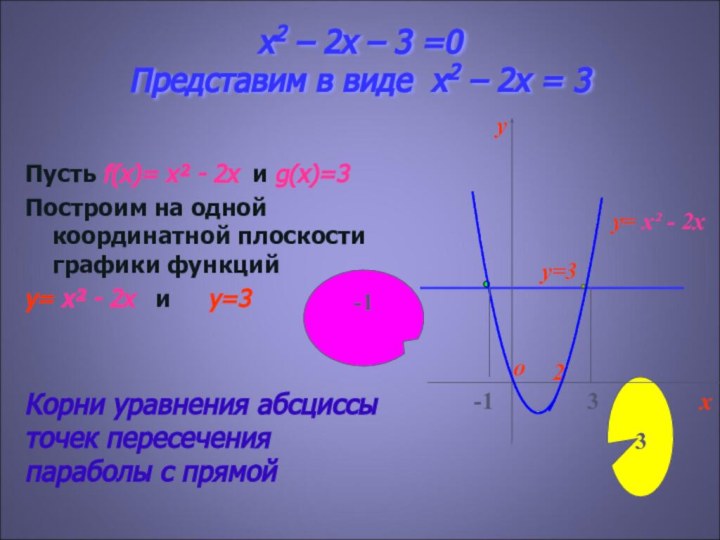
Корни уравнения абсциссы точек пересечения параболы с прямой

y=3

y= х² - 2х

y

х

о

2


-1

3

Слайд 22 Алгоритм решения квадратного уравнения графическим способом
Способ 3
(выделение

Алгоритм решения квадратного уравнения графическим способомСпособ 3 (выделение полного квадрата)Преобразовать уравнение

полного квадрата)
Преобразовать уравнение к виду
a(x+l)2 = m
Построить:

параболу y = a(x+l)2 и прямую y = m
Найти абсциссы точек пересечения графиков функций.

Слайд 23 Выделение квадрата двучлена.

x2 – 2x

Выделение квадрата двучлена. x2 – 2x + 1 = 3

+ 1 = 3 + 1
(

x –1)2=4.

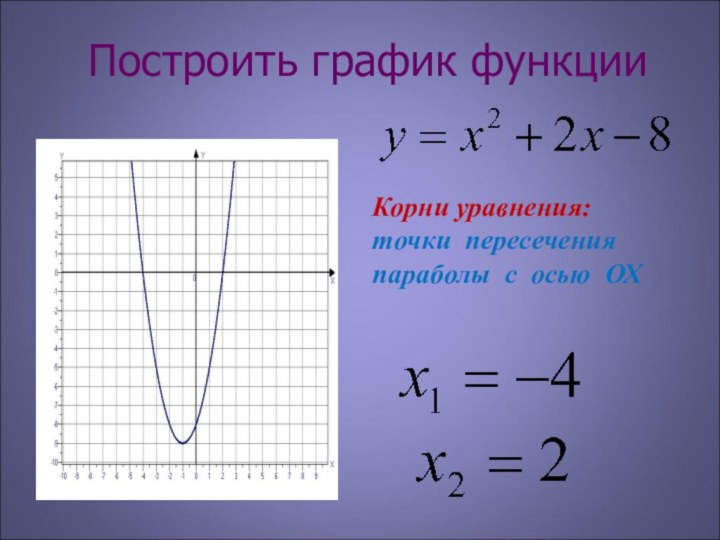
x2 – 2x = 3

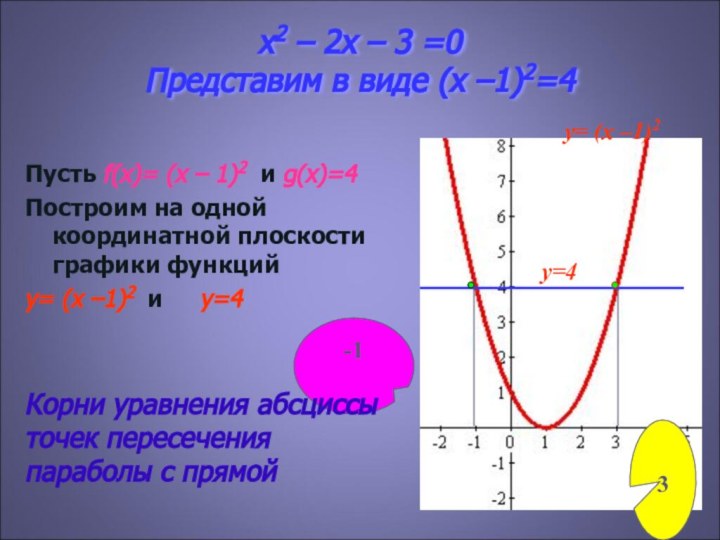
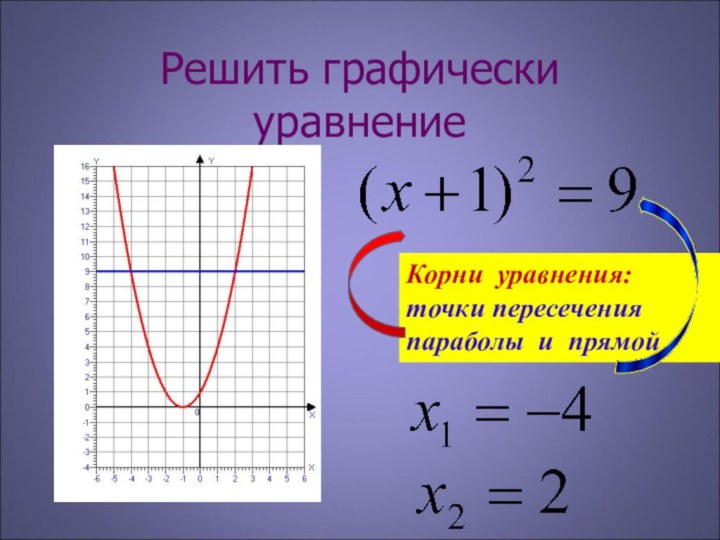
( x –1)2 - 4 = 0

( x –1)2 - 2² = 0

( x –1 – 2) ( x –1 + 2 ) = 0

( x –3 ) ( x + 1 ) = 0

x –3 = 0

x + 1 = 0

x = 3

x = - 1

Слайд 24 x2 – 2x – 3 =0 Представим в

x2 – 2x – 3 =0 Представим в виде (x –1)2=4Пусть

виде (x –1)2=4
Пусть f(x)= (x – 1)2 и g(x)=4
Построим

на одной координатной плоскости графики функций
y= (x –1)2 и y=4



-1


3

Корни уравнения абсциссы точек пересечения параболы с прямой

y=4

y= (x –1)2

Слайд 25 Решите графически уравнение
Группа А
Группа С
Группа В
х²

Решите графически уравнениеГруппа АГруппа СГруппа В х² + 2х – 8=

+ 2х – 8= 0
4х² - 8х + 3=

0

3х² + 2х – 1= 0

Слайд 26
Сколько нам открытий чудных готовит просвещения дух?

Сколько нам открытий чудных готовит просвещения дух?

Слайд 27 Решить графически уравнение

Решить графически уравнение

Слайд 28 Как решить уравнение?
Построить график квадратичной функции и абсциссы

Как решить уравнение?Построить график квадратичной функции и абсциссы точек пересечения параболы

точек пересечения параболы с осью x будут являться корнями

уравнения.
Выполнить преобразование уравнения, рассмотреть функции, построить графики этих функций, установить точки пересечения графиков функций, абсциссы которых и будут являться корнями уравнения.

Слайд 29 Решить графически уравнение

Решить графически уравнение

Слайд 30 Построить график функции

Построить график функции

Слайд 31 Построить график функции

Построить график функции

Слайд 32 Корни уравнения: абсциссы точек пересечения графиков функций


Корни уравнения: абсциссы точек пересечения графиков функций

Слайд 33 Построить график функции
Корни уравнения:
точки пересечения
параболы с осью

Построить график функцииКорни уравнения:точки пересечения параболы с осью ОХ

ОХ

Слайд 34 Решить графически уравнение
Корни уравнения:
точки пересечения
параболы и прямой

Решить графически уравнениеКорни уравнения:точки пересечения параболы и прямой

Слайд 35 Решить графически уравнение
Корни уравнения:
точки пересечения
параболы и прямой


Решить графически уравнениеКорни уравнения:точки пересечения параболы и прямой

Слайд 36 Итог
Познакомились:
с графическим методом решения квадратных уравнений;
с

Итог Познакомились: с графическим методом решения квадратных уравнений;с различными способами графического

различными способами графического решения квадратных уравнений.
закрепили знания по построению

графиков различных функций.

Слайд 37 Заключительное слово учителя:
«Чем больше и глубже вам удастся

Заключительное слово учителя:«Чем больше и глубже вам удастся усвоить азы математики

усвоить азы математики и научиться пользоваться ее методами, тем

дальше и быстрее вы сумеете продвинуться в использовании математических средств в той области деятельности, которой займетесь после школы»
  • Имя файла: graficheskoe-reshenie-kvadratnyh-uravneniy.pptx
  • Количество просмотров: 183
  • Количество скачиваний: 0
- Предыдущая Презентация Интеллект - карты на уроке французского языка
Следующая - Современные проблемы преподования информатики в условия реализации ФГОС

Похожие презентации

Презентация по математике (алгебра) Функция у=к/х (8 класс) Презентация по математике (алгебра) Функция у=к/х (8 класс) 163
Немного логики Немного логики 155
Презентация по алгебре и началам анализа на тему Числовая окружность на координатной плоскости (10 класс) Презентация по алгебре и началам анализа на тему Числовая окружность на координатной плоскости (10 класс) 205
Презентация и конспект урока алгебры в 7 классе Возведение в квадрат суммы и разности двух выражений Презентация и конспект урока алгебры в 7 классе Возведение в квадрат суммы и разности двух выражений 254
Пересечение и объединение множеств (8 класс) Пересечение и объединение множеств (8 класс) 188
Презентация по геометрии на тему :Симметрия в пространстве (10класс) Презентация по геометрии на тему :Симметрия в пространстве (10класс) 134
Деление дробей Деление дробей 154
Презентация открытого урока по теме Разложение многочлена на множители Презентация открытого урока по теме Разложение многочлена на множители 186
Презентация Математическая викторина для 6-7 классов Презентация Математическая викторина для 6-7 классов 196
Умножение одночлена на многочлен Умножение одночлена на многочлен 172
Числовая окружность на координатной плоскости. 10 класс Числовая окружность на координатной плоскости. 10 класс 215
Иррациональные числа Иррациональные числа 176
Методы решения иррациональных уравнений Методы решения иррациональных уравнений 188
Презентация к уроку алгебры в 8 классе Рациональные выражения Презентация к уроку алгебры в 8 классе Рациональные выражения 164
Квадратные уравнения Квадратные уравнения 192
Преобразование алгебраических выражений Преобразование алгебраических выражений 189
Презентация по математике на тему Иррациональные числа. Понятие комплексного числа. Презентация по математике на тему Иррациональные числа. Понятие комплексного числа. 186
Презентация по алгебре на тему Свойства арифметического корня Презентация по алгебре на тему Свойства арифметического корня 165
Комплексные числа в алгебраической форме Комплексные числа в алгебраической форме 135
Игра №2 Игры разума по заданиям ОГЭ (по заданиям 1 части) Игра №2 Игры разума по заданиям ОГЭ (по заданиям 1 части) 137
Презентация к дидактической игре Крестики-нолики. Алгебра. 7 класс Презентация к дидактической игре Крестики-нолики. Алгебра. 7 класс 142
Презентация внеклассного мероприятия по математике Презентация внеклассного мероприятия по математике 148
Презентация к уроку Исследование функции Презентация к уроку Исследование функции 151
Урок алгебры и начал анализа Урок алгебры и начал анализа 161
Решение задач В11 Решение задач В11 140
Определение производной Определение производной 143
Применение теории графов Применение теории графов 182
Использование производной для нахождения минимума/максимума в физике. Использование производной для нахождения минимума/максимума в физике. 166
Презентация по алгебре на тему Простейшие тригонометрические уравнения (10 класс) Презентация по алгебре на тему Простейшие тригонометрические уравнения (10 класс) 163