Презентация на тему Урок по теме Пирамиды

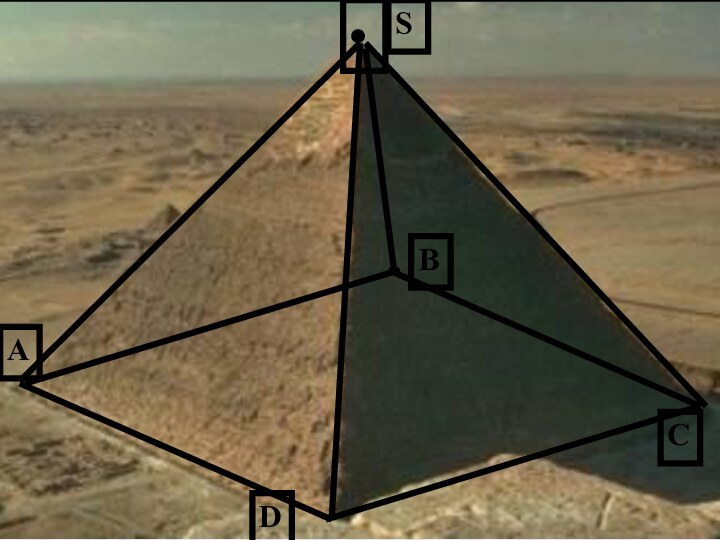
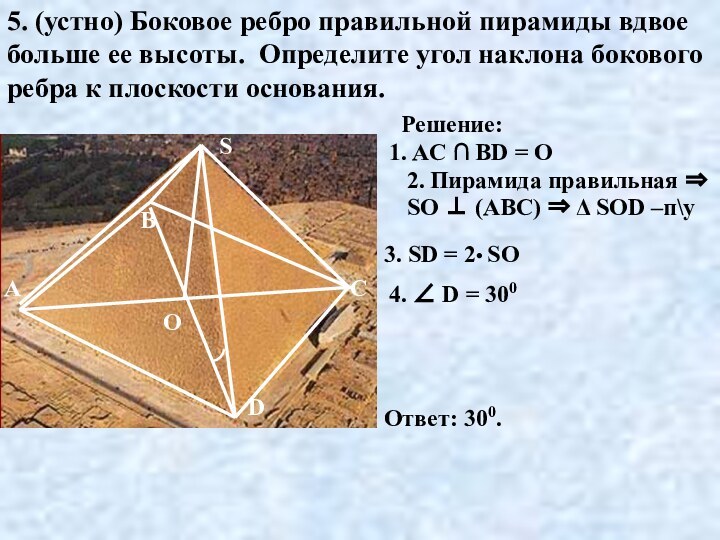
стороной 230м, тангенс угла наклона боковой грани к основанию

равен 1,2. Найти высоту самой высокой египетской пирамиды, если основание ее лежит в центре квадрата.

О

E

S

D

С

В

А

Решение:

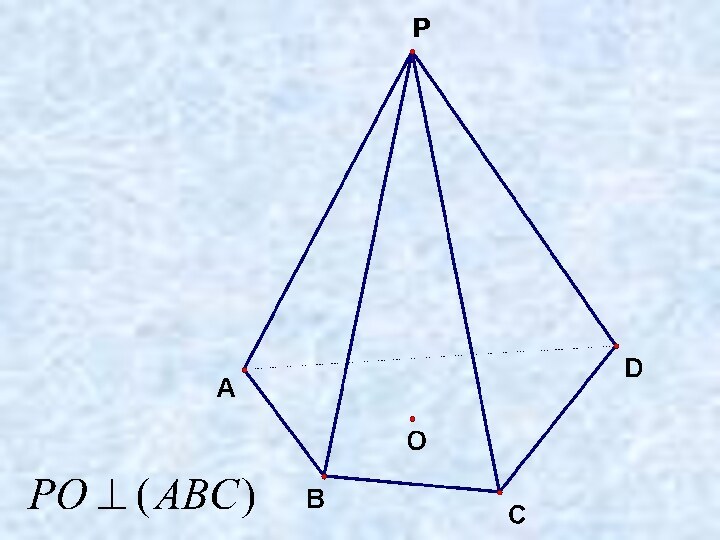
1. AC ∩ ВD = О

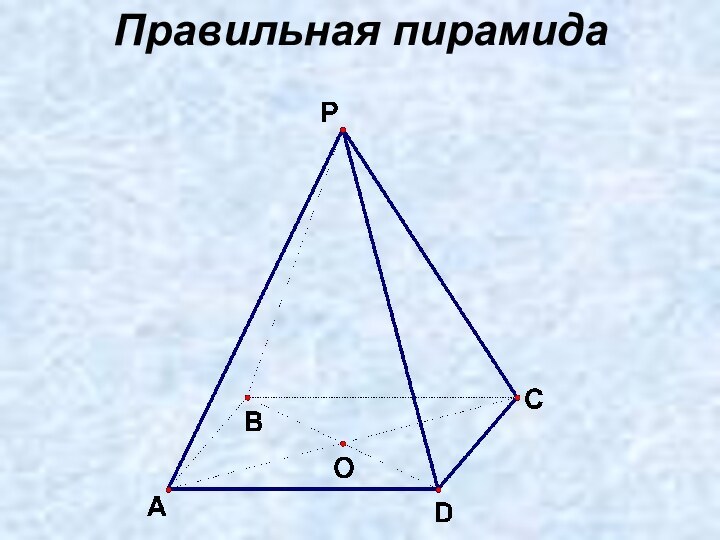
2. Пирамида правильная ⇒
SО ⊥ (АВС)

3. ОЕ ⎜⎜ АD ⇒ ОЕ ⊥ СD ⇒

4. SЕ ⊥ СD (по теореме о 3 перпендикулярах)

5. Δ SОЕ – п\у tg E = SО : ОЕ

6. ОЕ = 0,5АD =115м

7. SО = ОЕ • tg E = 115 • 1,2 = 138 м

Ответ: 138 м.

стороной 230м, высота пирамиды 138 м. Найти боковое ребро

самой высокой египетской пирамиды.

О

230 м

S

D

С

В

А

Решение:

1. AC ∩ ВD = О

3. Пирамида правильная ⇒
SО ⊥ (АВС)

4. Δ SОD – п\у

по т. Пифагора DS2 = DО2+ОS2 = 26450 + 1382=
= 26450 +19044 = 45494
DS ≈ 213 м

Ответ: 213 м.

2. Δ АОD – п\у, р\б

по т. Пифагора
АD2 = DО2+ОА2
2ОD2= 2302 = 52900
ОD2 = 26450

правильного тетраэдра с ребром 1?
Решение
1. Sпов=4Sтр
2. Sтр = 0,5а2sin600




Ответ:

3. Sпов=4 • 0,5а2sin600 =
=

основания которой равна 230 м и высота 138 м.


О
E
S
D
С
В
А
Решение:
2.

AC ∩ ВD = О

3. Пирамида правильная ⇒
SО ⊥ (АВС)

4. ОЕ ⎜⎜ СD ⇒ ОЕ ⊥ АD ⇒

5. SЕ ⊥ АD (по теореме о 3 перпендикулярах)

6. Δ SОЕ – п\у
по т. Пифагора
ЕS2 = ЕО2+ОS2 = 1152 + 1382 =
= 13225 +19044 = 32269
ЕS ≈ 180

7. ES - высота ΔАSD

SАSD = 0,5 ЕS•АD = 0,5 •180 • 230 =20700 м2

Ответ: 82800 м2

1. Sб.пов=4Sтр

8. Sб.пов=4Sтр = 4 • 20700 = 82800 м2

ее высоты. Определите угол наклона бокового ребра к плоскости

основания.

О

S

D

С

В

А

Решение:

1. AC ∩ ВD = О

2. Пирамида правильная ⇒
SО ⊥ (АВС) ⇒ Δ SОD –п\у

4. ∠ D = 300

Ответ: 300.

3. SD = 2• SO

и точки М и N, лежащие на ребрах AB

и BC тетраэдра ABCD

1.MN

2.MD

3.DN

4.Искомое сечение - ∆MDN.

•

•

•

M

N

B

М и прямую АС.

М


1. МА
2. МС
3. АМС - искомое

точки.
В
А
С
S


К
Р
F




1. РК
2. КF
3. КF ∩ SС = N
N
4. РN

∩ ВС = D

D

5. DF

6. PKFD - искомое

точки.
А
B
C
D
S
M
N
K



X
P
Y
Q




1. MN
2. MN ∩ ВС = Х
3. КХ ∩

DС = Р

4. NP

5. КХ ∩ АВ = Y

6. MY ∩ AS = Q

7. QK

8. QMNPK искомое

точки M,N,P, лежащие , соответственно, на ребрах AD,DC и

CB тетраэдра. Причем M и N заданы так, что прямые MN и AC не параллельны.

В

М

N

Р

1. MN

2. NP

3. MN ∩ AC = Q

Q

4. PQ ∩ AB = S

S

5. S M

6. SMNP – искомое сечение

H равна стороне основания a, то боковые ребра составляют

с плоскостью основания углы в 600. Верно ли это утверждение?
2). Сторона квадрата равна 10 см. Доказать, что нельзя, используя его в качестве основания, построить правильную четырехугольную пирамиду с боковым ребром 7 см.
3). Доказать или опровергнуть утверждение: «если в пирамиде все ребра равны, то пирамида правильная».