Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему по математике на тему:Решение тригонометрических уравнений

Содержание

2. Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает. (У. У. Сойер)
3. sin x = 1cos x = 0sin 4x – sin 2x = 0Удачи!Решение тригонометрических уравнений
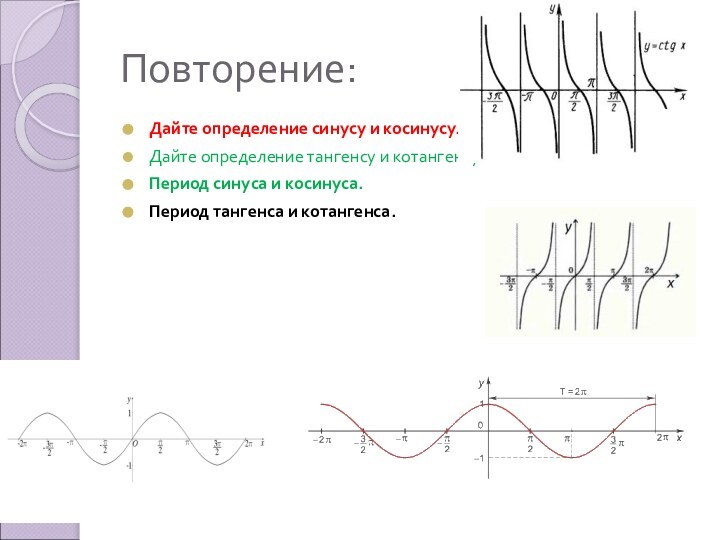
4. Повторение:Дайте определение синусу и косинусу.Дайте определение тангенсу и котангенсу.Период синуса и косинуса.Период тангенса и котангенса.
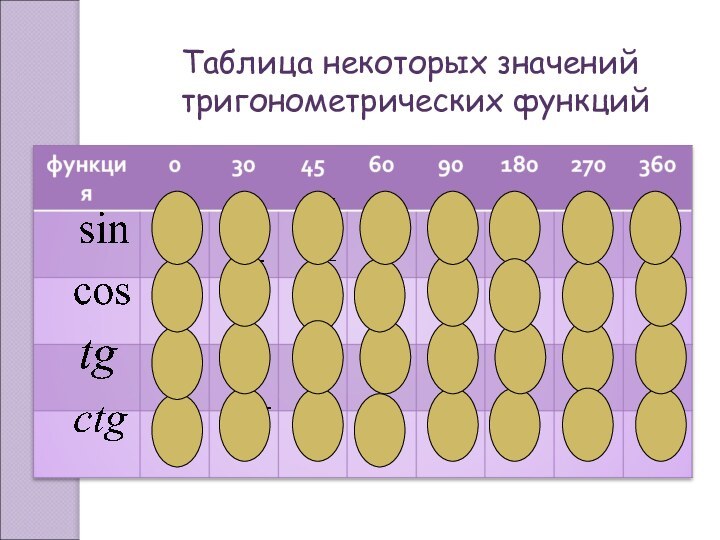
5. Таблица некоторых значений тригонометрических функций
6. Таблица перевода градусов в радианы
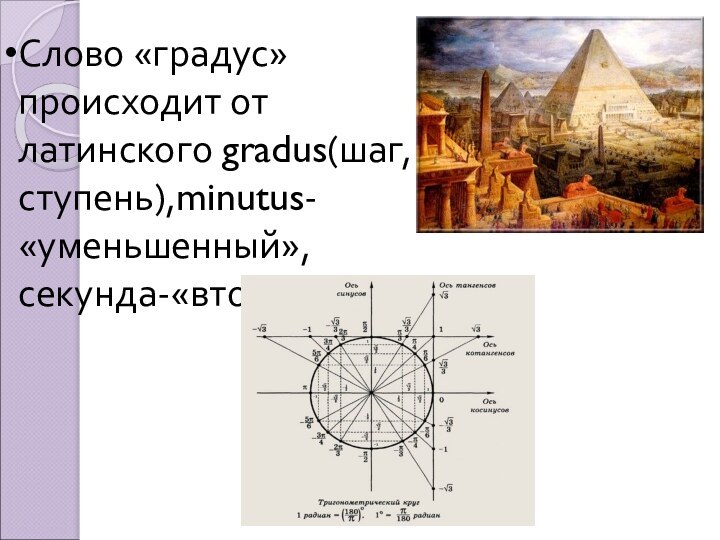
7. Слово «градус» происходит от латинского gradus(шаг, ступень),minutus-«уменьшенный»,секунда-«вторая»
8. В какой четверти лежит угол α, если выполняется условие sinα>0, cosα
9. Закончите предложение: cos(π/2 +α)=… (-Sinα)
10. Закончите 2sinαcosα (sin2α)
11. Может ли быть верным равенство sin²α
12. Вычислите sin²α + tgα∙сtgα + cos²α (2)
13. Какие значения может принимать sinх? ( от -1 до 1 включительно)
14. Закончите предложение cos²α - sin²α = ( cos2α)
15. Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол)
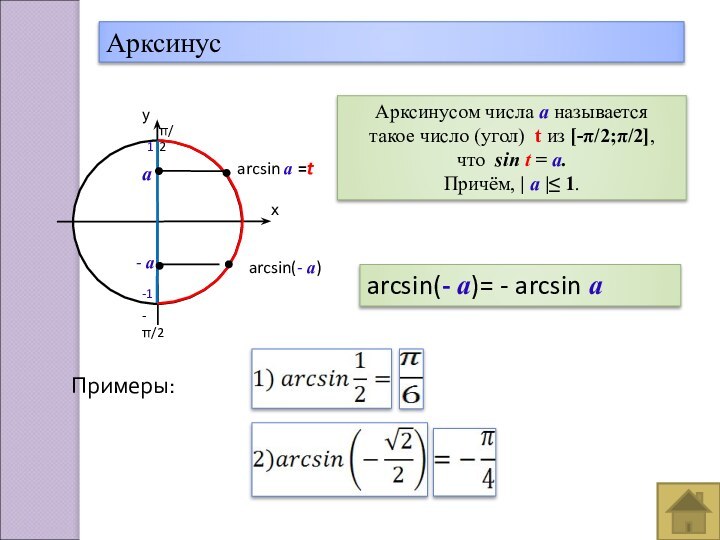
16. Арксинус
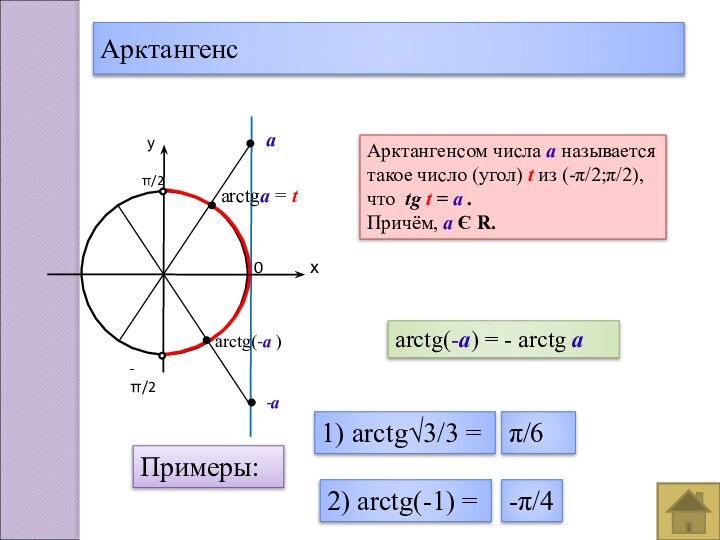
17. Арктангенс0arctgа = tАрктангенсом числа а называетсятакое число
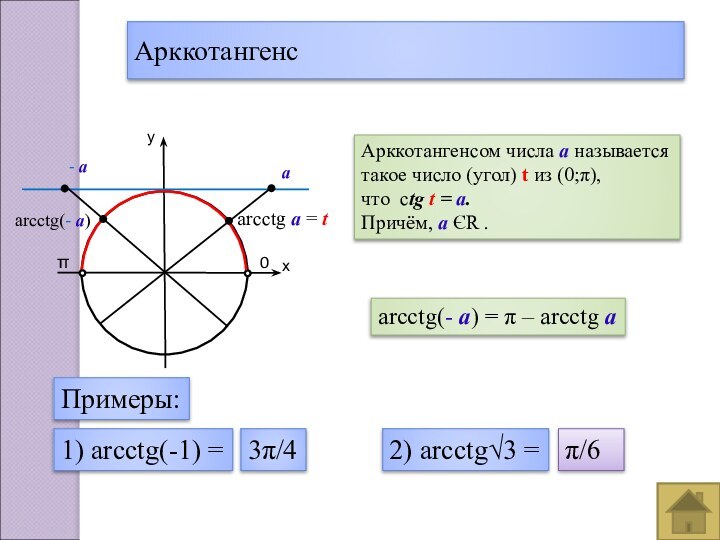
18. Арккотангенсух0πarcctg а = tАрккотангенсом числа а называетсятакое
20. Определение.Уравнения вида f(x) = а, где а
21. Уравнение cos t = a a)
22. Решите уравнение 1) cos х =
23. 3) cos 4x = 1
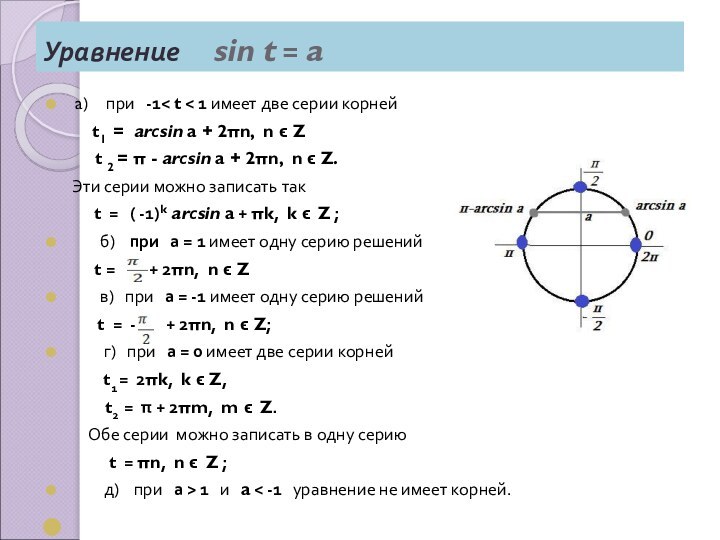
25. Уравнение sin t = a a)
26. Косинус- от сокращенного выражения , означающее на латинском «дополнительный синус».
27. sin х = Решите
29. 1) Задание 2. Найти корни уравнения:
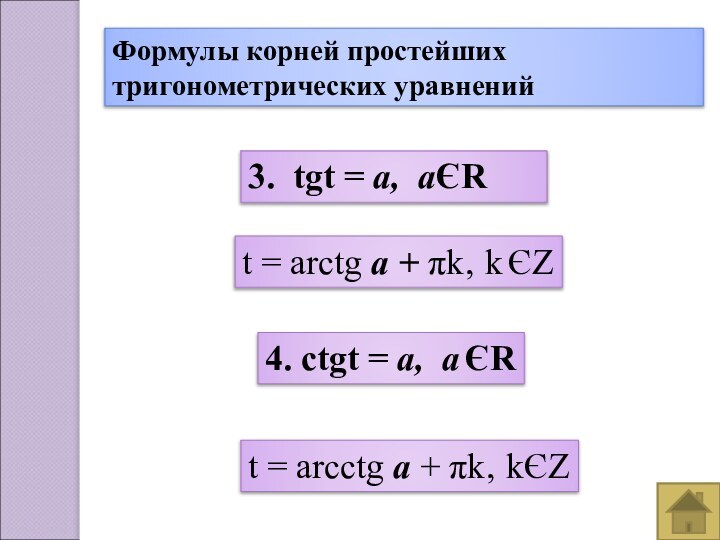
30. Формулы корней простейших тригонометрических уравнений3. tgt =
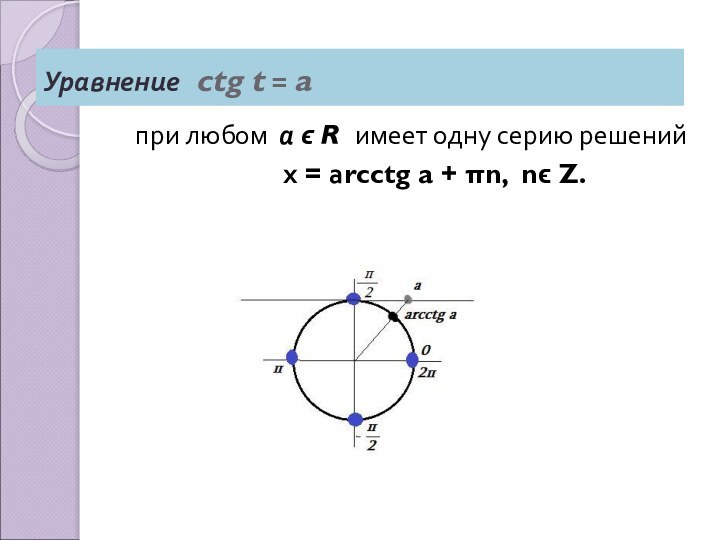
31. Уравнение ctg t = a при любом
32. Тангенсы(котангенсы)- возникли при решении задач об определении
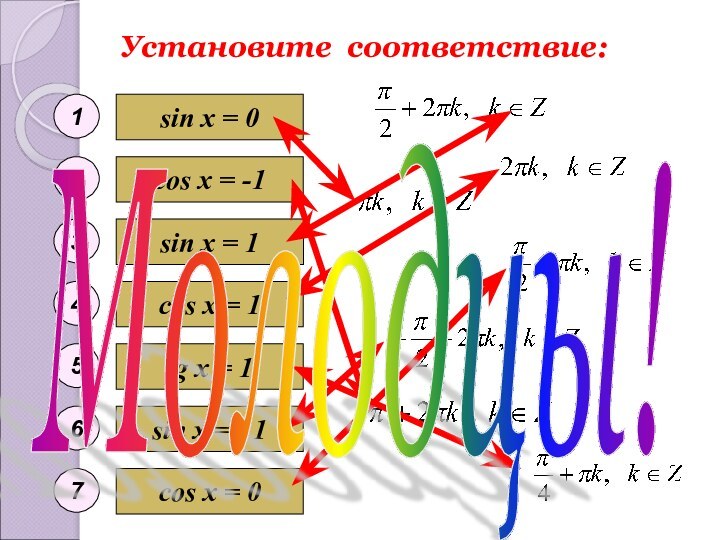
34. Установите соответствие(математическое лото):sin x = 0 sin
35. Установите соответствие:sin x = 0 sin x
36. Вариант 1№136(а),стр .71№139(б),стр.72Самостоятельная работаВариант 2№136(б),стр .71№139(а),стр.72
37. Ответы:
39. АКТИВНОСТЬ - ОТ 0
40. Читаю мыслиЗапиши любое однозначное или двузначное натуральное числоУмножь на 2Прибавь 12Раздели 2Вычти исходное число
41. Продолжите фразу :Сегодня на уроке я повторил
42. Скачать презентацию
43. Похожие презентации

Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает. (У. У. Сойер)

Главная
Алгебра
Презентация по математике на тему:Решение тригонометрических уравнений

Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает. (У. У. Сойер)

sin x = 1cos x = 0sin 4x – sin 2x = 0Удачи!Решение тригонометрических уравнений

Повторение:Дайте определение синусу и косинусу.Дайте определение тангенсу и котангенсу.Период синуса и косинуса.Период тангенса и котангенса.

Таблица некоторых значений тригонометрических функций

Слово «градус» происходит от латинского gradus(шаг, ступень),minutus-«уменьшенный»,секунда-«вторая»

В какой четверти лежит угол α, если выполняется условие sinα>0, cosα

Закончите предложение: cos(π/2 +α)=… (-Sinα)

Может ли быть верным равенство sin²α + cos²α = 3/2 ?

Какие значения может принимать sinх? ( от -1 до 1 включительно)

Закончите предложение cos²α - sin²α = ( cos2α)

Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол) t из [0;π], чтоcos t

Арктангенс0arctgа = tАрктангенсом числа а называетсятакое число (угол) t из (-π/2;π/2), что

Арккотангенсух0πarcctg а = tАрккотангенсом числа а называетсятакое число (угол) t из (0;π),

Презентация по математике на тему:Решение тригонометрических уравнений

Определение.Уравнения вида f(x) = а, где а – данное число, а f(x)

Косинус- от сокращенного выражения , означающее на латинском «дополнительный синус».

Формулы корней простейших тригонометрических уравнений3. tgt = а, аЄR t = arctg

Уравнение ctg t = a при любом а ϵ R имеет

Тангенсы(котангенсы)- возникли при решении задач об определении длины тени еще в 10

Установите соответствие(математическое лото):sin x = 0 sin x = - 1 sin

Установите соответствие:sin x = 0 sin x = - 1 sin x

Вариант 1№136(а),стр .71№139(б),стр.72Самостоятельная работаВариант 2№136(б),стр .71№139(а),стр.72

Читаю мыслиЗапиши любое однозначное или двузначное натуральное числоУмножь на 2Прибавь 12Раздели 2Вычти исходное число

Продолжите фразу :Сегодня на уроке я повторил …Сегодня на уроке я узнал

П.9, № 138(А,Б),№145(В,Г)ДОМАШНЕЕ ЗАДАНИЕ:

Слайды презентации

Слайд 2
Стоит только показать, что какая-либо вещь невозможна, как

найдется математик, который ее сделает. (У. У. Сойер)

Слайд 3

sin x = 1
cos x = 0
sin 4x

– sin 2x = 0
Удачи!
Решение тригонометрических уравнений

Слайд 4 Повторение:
Дайте определение синусу и косинусу.
Дайте определение тангенсу и

котангенсу.
Период синуса и косинуса.
Период тангенса и котангенса.

Слайд 5 Таблица некоторых значений
тригонометрических функций

Слайд 6 Таблица перевода градусов в радианы

Слайд 7 Слово «градус» происходит от латинского gradus(шаг, ступень),minutus-«уменьшенный»,секунда-«вторая»

Слайд 8

В какой четверти лежит угол α, если выполняется

условие sinα>0, cosα

Слайд 9

Закончите предложение: cos(π/2 +α)=…

(-Sinα)

Слайд 10

Закончите 2sinαcosα
(sin2α)

Слайд 11
Может ли быть верным равенство
sin²α

+ cos²α = 3/2 ?

( Нет)

Слайд 12

Вычислите
sin²α + tgα∙сtgα + cos²α

(2)

Слайд 13
Какие значения может принимать sinх?

( от -1 до 1 включительно)

Слайд 14

Закончите предложение
cos²α - sin²α =

( cos2α)

Слайд 15 Арккосинус

0
π
1
-1
arccos(-а)
Арккосинусом числа а называется
такое число (угол) t

Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол) t из [0;π], чтоcos

из [0;π], что
cos t = а.
Причём, | а

|≤ 1.

arccos(- а) = π- arccos а

Примеры:

1)arccos(-1)

= π

2)arccos( )

Слайд 16 Арксинус

Примеры:

- а

arcsin(- а)= - arcsin а

Арксинусом числа а называется
такое число (угол) t из [-π/2;π/2],
что sin t = а.
Причём, | а |≤ 1.

Слайд 17 Арктангенс

0
arctgа = t
Арктангенсом числа а называется
такое число (угол)

Арктангенс0arctgа = tАрктангенсом числа а называетсятакое число (угол) t из (-π/2;π/2),

t из (-π/2;π/2),
что tg t = а .
Причём,

а Є R.

arctg(-а) = - arctg а

-а

arctg(-а )

Примеры:

1) arctg√3/3 =

π/6

2) arctg(-1) =

-π/4

Слайд 18 Арккотангенс

у
х

0
π
arcctg а = t
Арккотангенсом числа а называется
такое число

Арккотангенсух0πarcctg а = tАрккотангенсом числа а называетсятакое число (угол) t из

(угол) t из (0;π),
что ctg t = а.
Причём,

а ЄR .

arcctg(- а) = π – arcctg а

- а

arcctg(- а)

1) arcctg(-1) =

Примеры:

3π/4

2) arcctg√3 =

π/6

Слайд 19

Слайд 20 Определение.
Уравнения вида f(x) = а, где а –

Определение.Уравнения вида f(x) = а, где а – данное число, а

данное число, а f(x) – одна из тригонометрических функций,

называются простейшими тригонометрическими уравнениями.

Слайд 21 Уравнение cos t = a
a)

при -1< t < 1 имеет две

серии корней
t1 = arсcos a + 2πk, k ϵ Z
t 2 = - arсcos a + 2πm, m ϵ Z.
Эти серии можно записать так
t = ± arсcos a + 2πn, n ϵ Z ;
б) при а = 1 имеет одну серию решений
t = 2πn, n ϵ Z ;
в) при а = -1 имеет одну серию решений
t = π + 2πn, n ϵ Z ;
г) при а = 0 имеет две серии корней
t1 = + 2πk, k ϵ Z
t 2 = - + 2πm, m ϵ Z. Обе серии можно записать в одну серию
t = + πn, n ϵ Z.
д) при а > 1 и a < -1 уравнение не имеет корней.

Слайд 22 Решите уравнение
1) cos х =
2)

cos х = -

Слайд 23 3) cos 4x = 1

4x = 2πn, n ϵ Z

Решите уравнение

Слайд 24

5)
Решите уравнение

.

Слайд 25 Уравнение sin t = a
a)

при -1< t < 1 имеет

две серии корней
t1 = arсsin a + 2πn, n ϵ Z
t 2 = π - arсsin a + 2πn, n ϵ Z.
Эти серии можно записать так
t = ( -1)k arсsin a + πk, k ϵ Z ;
б) при а = 1 имеет одну серию решений
t = + 2πn, n ϵ Z
в) при а = -1 имеет одну серию решений
t = - + 2πn, n ϵ Z;
г) при а = 0 имеет две серии корней
t1 = 2πk, k ϵ Z,
t2 = π + 2πm, m ϵ Z.
Обе серии можно записать в одну серию
t = πn, n ϵ Z ;
д) при а > 1 и a < -1 уравнение не имеет корней.