углов с сонаправленными сторонами.
Научиться находить
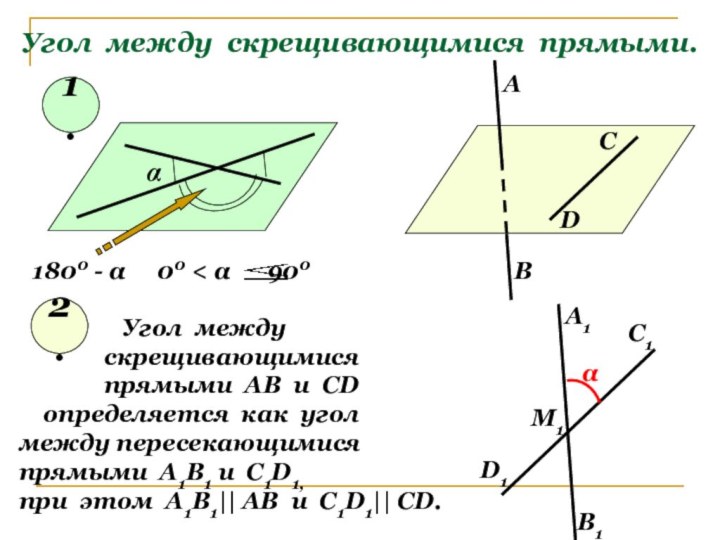
угол между
прямымив пространстве.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





Нет
Да
Нет
Нет
Да
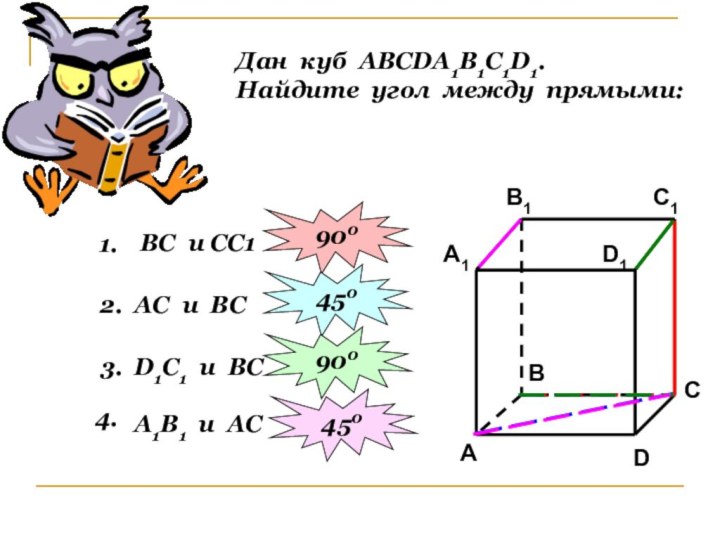
АВ скрещивается с А1В1
А
В
С
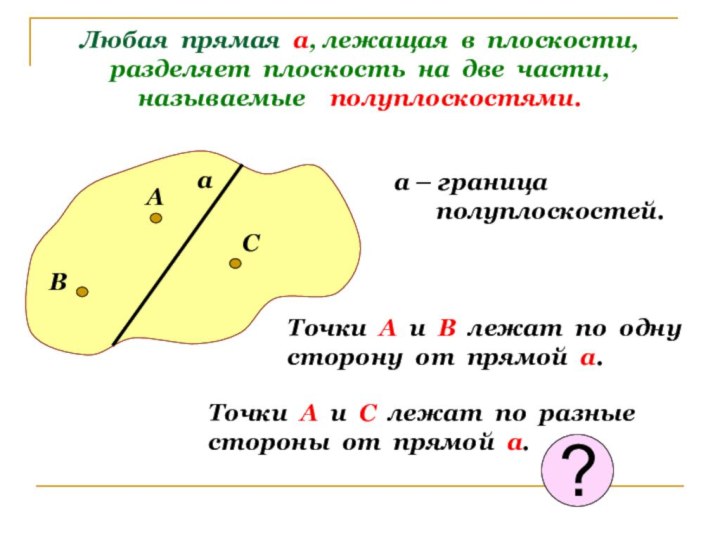
Точки А и В лежат по одну
сторону от прямой а.
Точки А и С лежат по разные
стороны от прямой а.
?
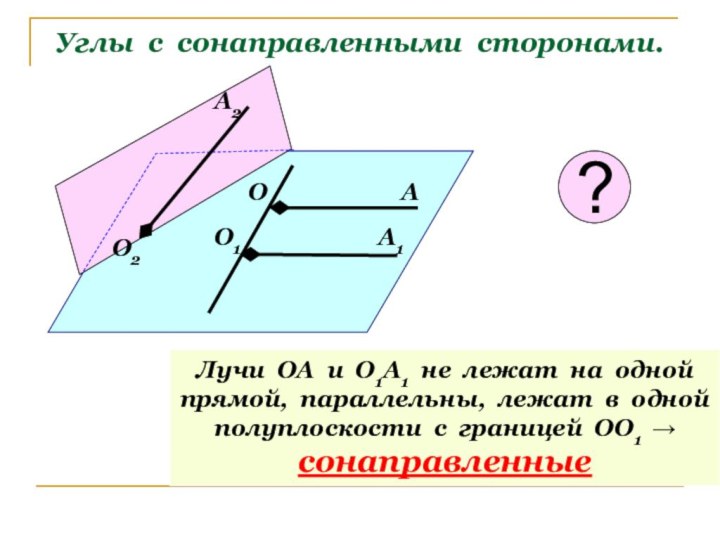
А2
О2
?
Доказать:
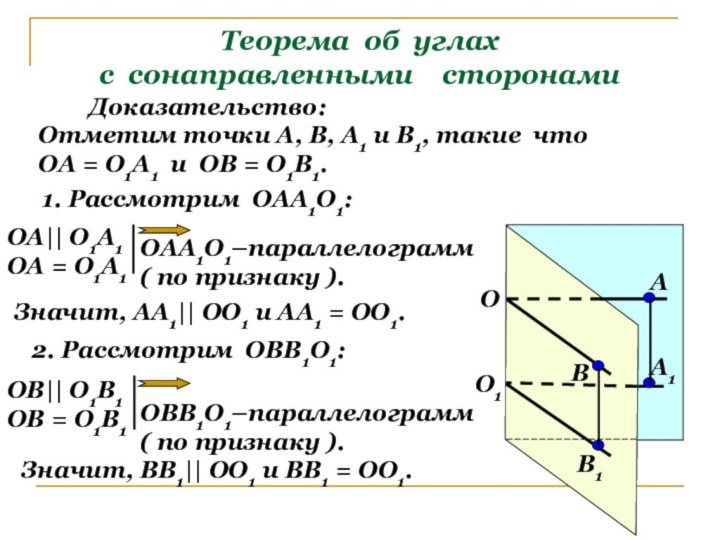
1. Рассмотрим ОАА1О1:
ОА|| О1А1
ОА = О1А1
ОАА1О1–параллелограмм
( по признаку ).
2. Рассмотрим ОВВ1О1:
Значит, АА1|| ОО1 и АА1 = ОО1.
ОВ|| О1В1
ОВ = О1В1
ОВВ1О1–параллелограмм
( по признаку ).
Значит, ВВ1|| ОО1 и ВВ1 = ОО1.
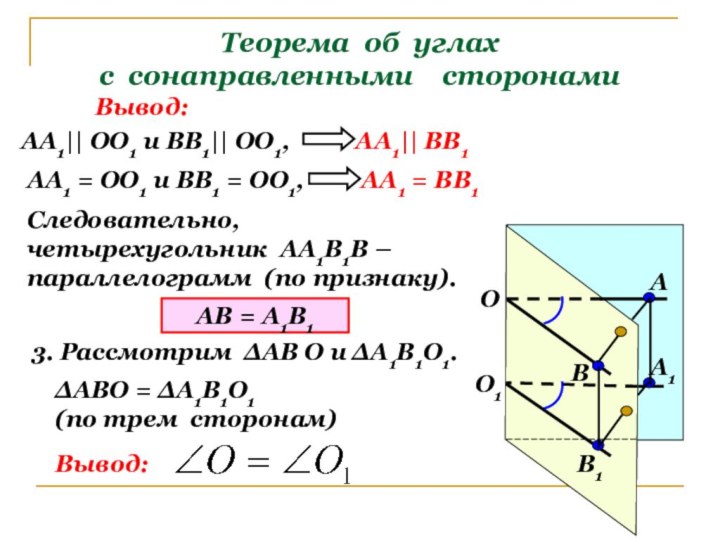
АА1 = ВВ1
Следовательно,
четырехугольник АА1В1В –
параллелограмм (по признаку).
АВ = А1В1
3. Рассмотрим ∆АВ О и ∆А1В1О1.
∆АВО = ∆А1В1О1
(по трем сторонам)
Вывод:
А
В
D
С
А1
В1
С1
D1
α
М1
2. Являются ли углы А1М1D1 и А2М2D2
углами с соответственно
параллельными сторонами?
?
Вывод:
1.
Величина угла между скрещивающимися
прямыми не зависит от выбора точки.
3.
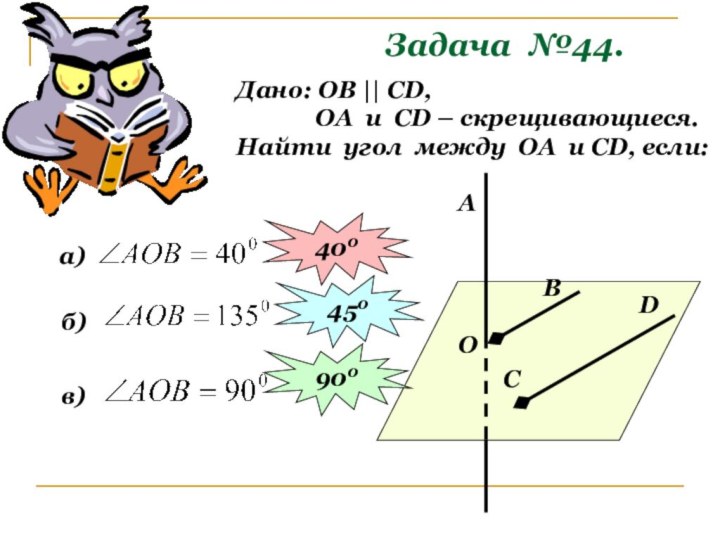
О
В
C
D
A
а)
400
б)
450
в)
900