.
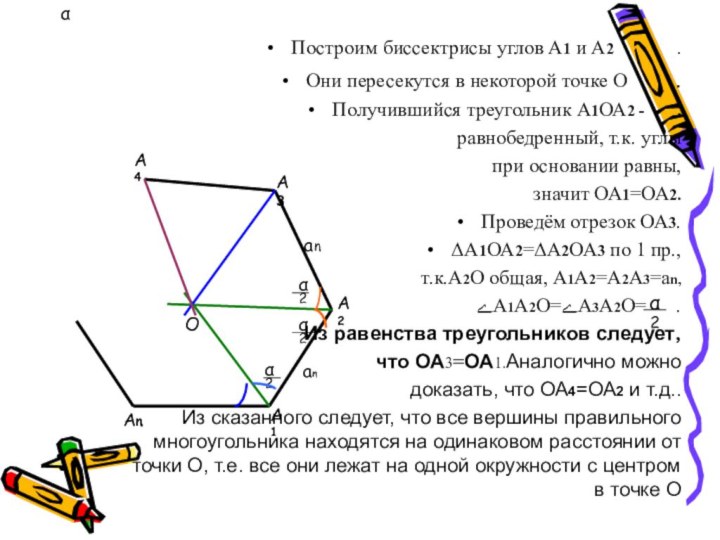
Они пересекутся в некоторой точке
О .Получившийся треугольник А1ОА2 - .
равнобедренный, т.к. углы
при основании равны,
значит ОА1=ОА2.
Проведём отрезок ОА3.
ΔА1ОА2=ΔА2ОА3 по 1 пр.,
т.к.А2О общая, А1А2=А2А3=аn,
ےА1А2О=ےА3А2О= .
Из равенства треугольников следует,
что ОА3=ОА1.Аналогично можно
доказать, что ОА4=ОА2 и т.д..
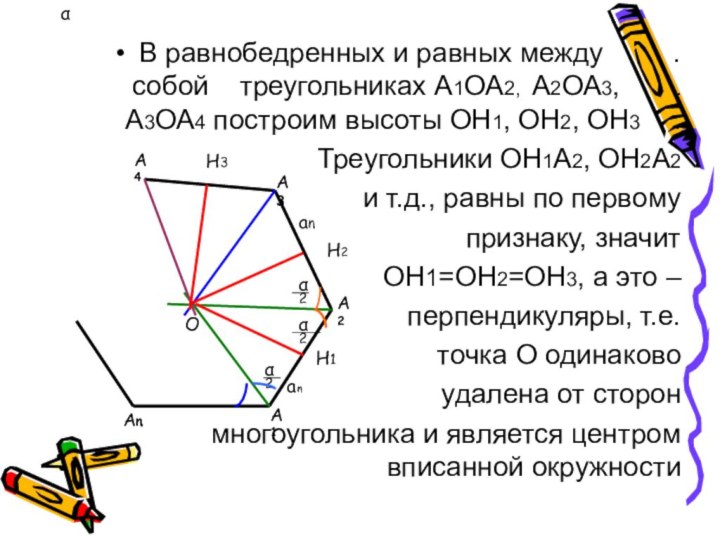
Из сказанного следует, что все вершины правильного многоугольника находятся на одинаковом расстоянии от точки О, т.е. все они лежат на одной окружности с центром в точке О
α
2
аn
аn
α
2
α
2
О
А1
А2
А4
А3
α
2
Аn