Презентация на тему Многогранник.

числа плоских многоугольников.
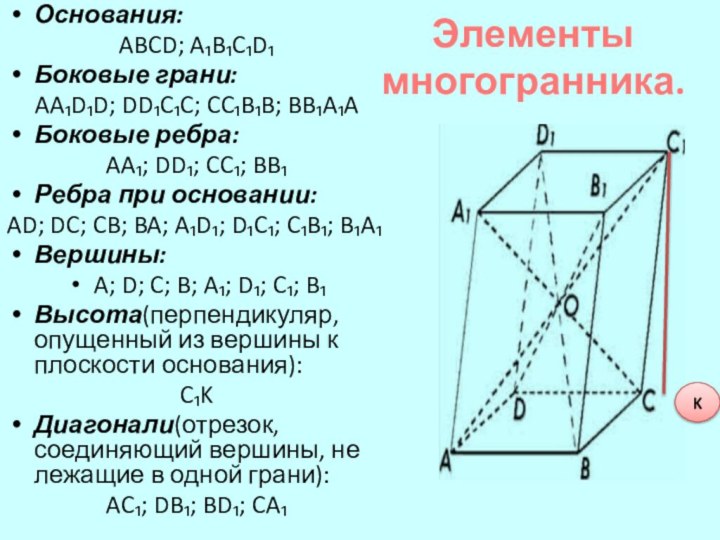
Эти многоугольники называются гранями многогранника.
Стороны многоугольников –

ребрами многогранника.
Вершины или точки, в которых сходятся ребра – вершинами многогранника.

В₁ С₁

A₁ D₁



B C

A D

DD₁; CC₁; BB₁
Ребра при основании:
AD; DC; CB; BA; A₁D₁;

D₁C₁; C₁B₁; B₁A₁
Вершины:
A; D; C; B; A₁; D₁; C₁; B₁
Высота(перпендикуляр, опущенный из вершины к плоскости основания):
C₁K
Диагонали(отрезок, соединяющий вершины, не лежащие в одной грани):
AC₁; DB₁; BD₁; CA₁

K

сторону от плоскости любой его грани.
Невыпуклый

(треугольная призма)
или высота попадает в центр основания (четырехугольная

пирамида).

Наклонные, если боковое ребро не перпендикулярно плоскости основания (треугольная призма)
Или высота не попадает в центр основания (треугольная пирамида).

многоугольник (многоугольник, у которого все стороны равны).
Неправильные, если в

основании лежит неправильный многоугольник.

Оформим дано.
2. На чертеже покажем диагональ BD₁ и обозначим

ребро D₁C₁=4.
3. Определим треугольник, куда входит диагональ BD₁: ∆DD₁B – прямоугольный. Почему? Для треугольника BD₁ - гипотенуза. Вычислим ее по теореме Пифагора:
BD₁²=DD₁²+BD². (3)
В данном выражении неизвестен катет BD.
4. Определим треугольник, в который входит BD: ∆ADB – прямоугольный. Почему? По теореме Пифагора вычислим BD - гипотянуза.
BD²=AB²+AD². (4)
5. Подставляя значение (4) в (3), получим BD₁²=DD₁²+AB²+AD².

6. Ответ:

4

измерения параллелепипеда, где
a – длина,
b – ширина,
c - высота;

2. Квадрат диагонали равен сумме квадратов его измерений.
d²=a²+b²+c²

d

равна 80см.