называется правильной?
г) Что является основанием правильной
треугольной призмы?
д) Чем являются боковые грани призмы?
Прямой призмы? Правильной призмы?
Устно
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




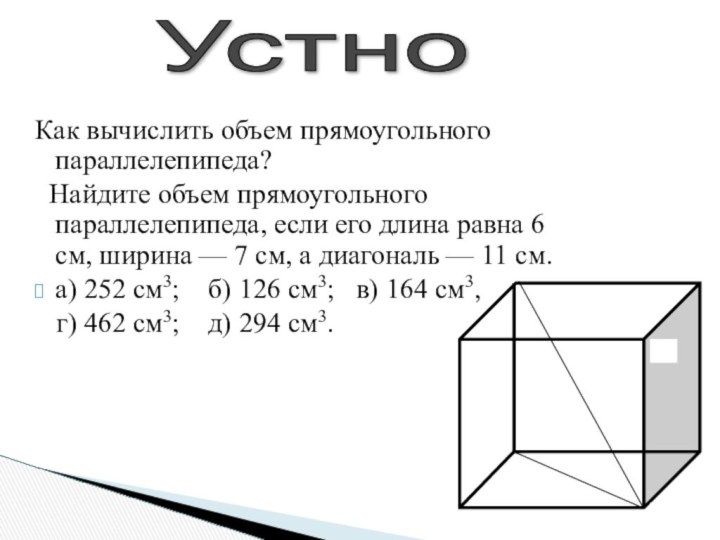
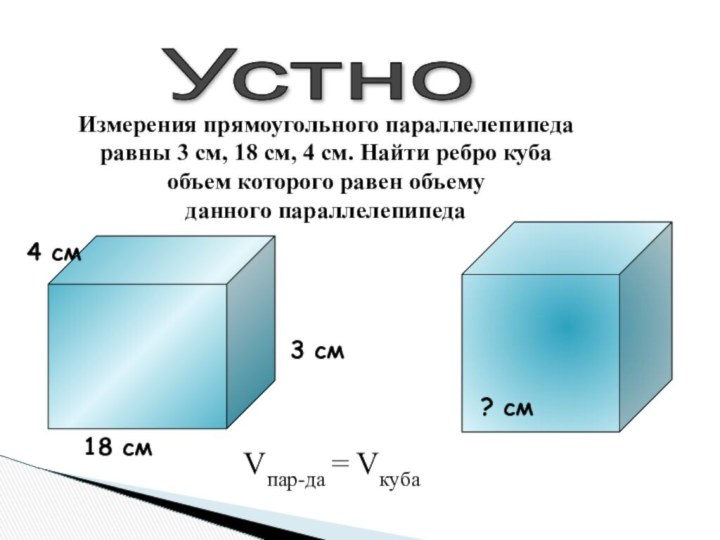


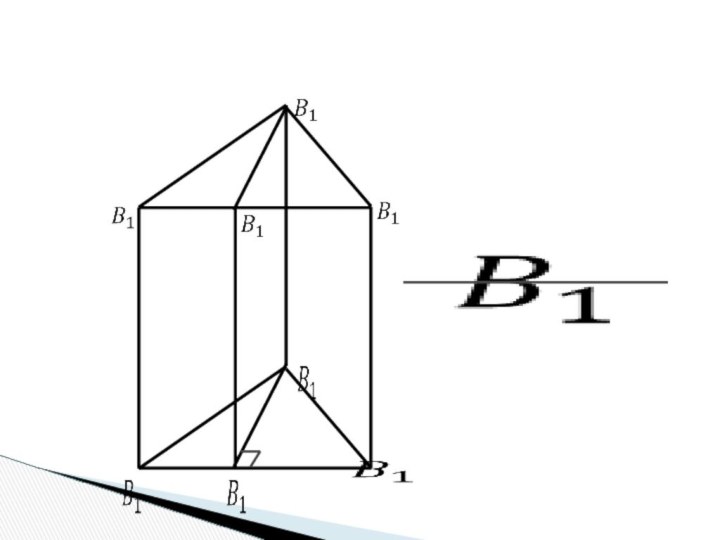
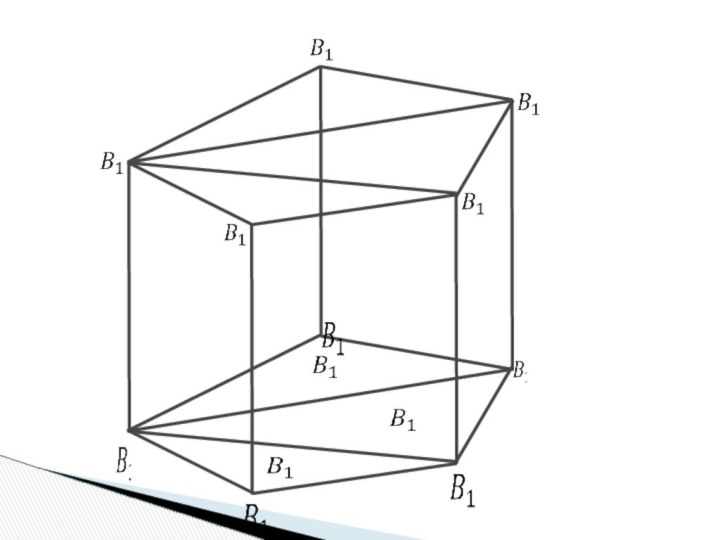




Устно
Выберите неверное утверждение
Устно
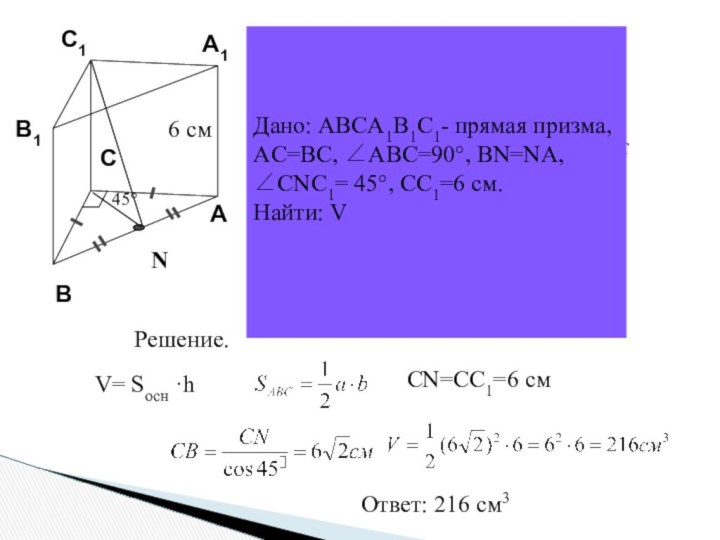
Боковое ребро равно 6 см.
45°
6 см
Найти объём призмы.
V= Sосн ·h
CN=CC1=6 cм
Решение.
Ответ: 216 см3
Дано: ABCA1B1C1- прямая призма,
AC=BC, ∠АВС=90°, BN=NA,
∠CNC1= 45°, СС1=6 см.
Найти: V
45°
Найти объём призмы.
Дано: ABCDA1B1C1D1- прямая призма,
ABCD – ромб, ∠ВАD=60°, BB1=2,
∠B1DВ= 45°.
Найти: V
Решение.
V= Sосн ·h
∆ABD - равносторонний
AB=BD=2, т. к. ∆B1BD - равнобедренный
Ответ:
8 см
30°
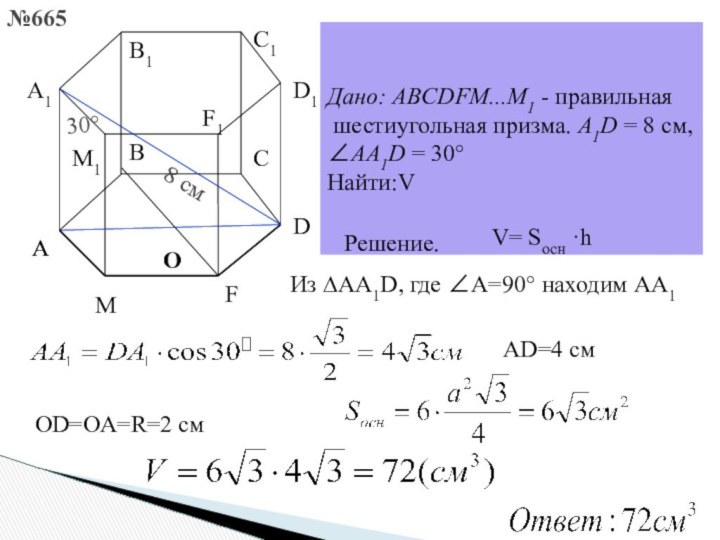
Дано: ABCDFM...M1 - правильная
шестиугольная призма. A1D = 8 см,
∠AА1D = 30°
Найти:V
Решение.
V= Sосн ·h
Из ∆AА1D, где ∠А=90° находим AА1
AD=4 см
О
OD=OA=R=2 см
Итог урока.