Презентация на тему Числовая окружность, 10 класс

числовой окружности.
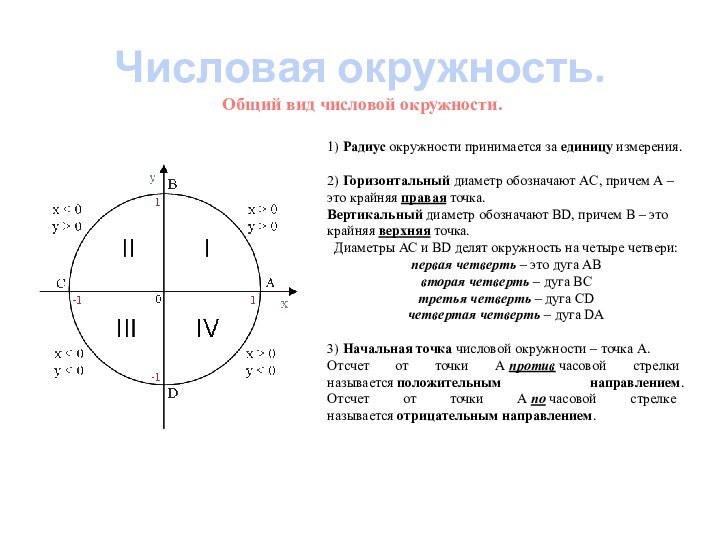
Общий вид числовой окружности.
Длина числовой окружности.
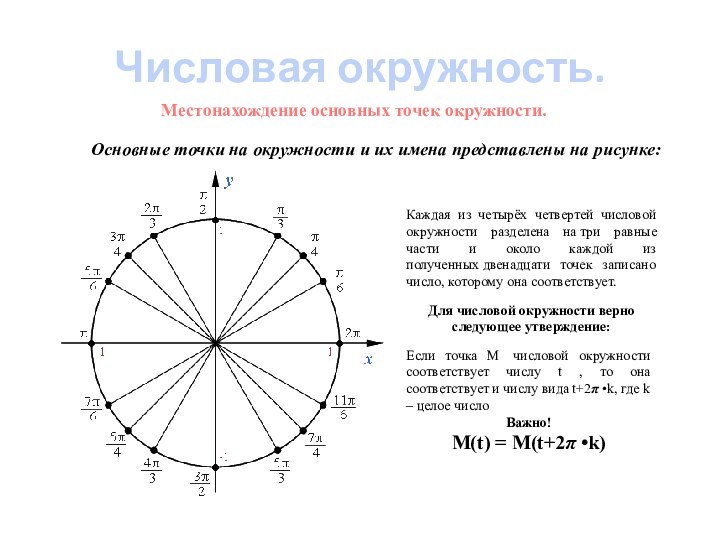
Местонахождение основных точек

окружности.

Примеры задач.

встречается движение по окружности. Например в спорте: соревнования велосипедистов,

которые проезжают определенный круг на время или соревнования гоночных автомобилей которым надо проехать наибольшее количество кругов за отведенное время.

по кругу длиной 400 метров. Спортсмен стартует в точке

А (рис. 1) и движется против часовой стрелки. Где он будет находится через 200м, 800м, 1500м.? А где провести финишную черту если бегуну пробежать 4195м.?

Рисунок 1.

Через 200м. бегун будет находиться в точке С, так как он пробежит ровно половину дистанции.

Пробежав 800м., бегун сделает ровно два круга и окажется в точке А.

1500м. это 3 круга по 400 м (1200м.) и еще 300 метров, то есть ¾ от беговой дорожки, финиш этой дистанции в точке D.

Где будет находиться наш бегун пробежав 4195м.? 10 кругов это 4000 метров, останется пробежать 195 метров, это на 5 метров меньше чем половина дистанции. Значит финиш будет в точки М, расположенной около точки С.

Решение:

соответствуют определенным действительным числам.

Единичной окружностью называют окружность радиуса 1.
 

за единицу измерения.

2) Горизонтальный диаметр обозначают AC, причем А

– это крайняя правая точка.  Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Диаметры АС и BD делят окружность на четыре четвери: первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA

3) Начальная точка числовой окружности – точка А.
Отсчет от точки А против часовой стрелки называется положительным направлением. Отсчет от точки А по часовой стрелке называется отрицательным направлением.

формуле:
Так как единичная окружность то
Если взять
то

длина окружности

может быть выражена числом

Длина каждой четверти равна

и их имена представлены на рисунке:
Каждая из четырёх четвертей

числовой окружности разделена на три равные части и около каждой из полученных двенадцати точек записано число, которому она соответствует.

Для числовой окружности верно следующее утверждение:

Если точка М  числовой окружности соответствует числу t , то она соответствует и числу вида t+2π •k, где k – целое число
Важно!
М(t) = M(t+2π •k)

М на две равные части, а точками К и

Р — на три равные части.
Чему равна длина дуги: AM, МВ, АК, КР, РB, АР, КМ?

Длина дуги АВ = π/2, разделив ее на две равные части точкой М, получим две дуги, длиной — π/4 каждая. Значит, AM = МВ = π/4

Дуга АВ разбита на три равные части точками К и Р, то длина каждой полученной части равна 1/3 · π/2, т. е. π/6 значит, АК = КР = РВ = π/6.

Дуга АР состоит из двух дуг АК и КР длиной — π/6. Значит, АР = 2 • π/6 = π/3

Осталось вычислить длину дуги КМ. Эта дуга получается из дуги AM исключением дуги АК. Таким образом, КМ = AM – АК = π/4 - π/6 = π/12

заданному числу: 2π , 7π/2 , π/4 , -3π/2.
Решение:
Числу

2π соответствует точка А, т.к. пройдя по окружности путь длиной 2π, т.е. ровно одну окружность, мы опять попадем в точку А

Числу 7π/2 соответствует точка D, т.к. 7π/2 = 2π +3π/2, т.е. двигаясь в положительном направлении, нужно пройти целую окружность и дополнительно путь длиной 3π/2, который закончится в точке D

Числу π/4 соответствует точка М, т.к. двигаясь в положительном направлении, нужно пройти путь в половину дуги АВ длиной π/2, который закончится в точке M.

Числу -3π/2 соответствует точка В, т.к. двигаясь в отрицательном направлении из точки А, нужно пройти путь длиной 3π/2, который закончится в точке В

б) -37π/6
Решение: Пользуясь формулой что число М(t) = M(t+2π

•k) (8 слайд) получим

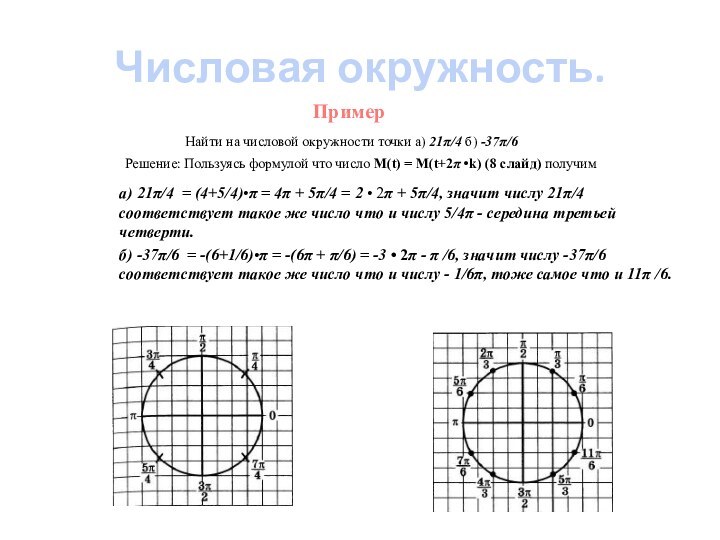
а) 21π/4 = (4+5/4)•π = 4π + 5π/4 = 2 • 2π + 5π/4, значит числу 21π/4 соответствует такое же число что и числу 5/4π - середина третьей четверти.

б) -37π/6 = -(6+1/6)•π = -(6π + π/6) = -3 • 2π - π /6, значит числу -37π/6 соответствует такое же число что и числу - 1/6π, тоже самое что и 11π /6.

окружности соответствуют точки, принадлежащие заданной дуге: а) ВА б)

МK

Решение:

а)Дуга ВА - это дуга с началом в точке В и концом в точке А при движении по окружности против часовой стрелки. Точка В соответственно равна π/2, а точка А равна 2π. Значит для точек t имеем: π/2 ≤ t ≤ 2π. Но согласно формуле на слайде 8 числам π/2 и 2π соответствуют числа вида π/2+2π •k и 2π+2π •k, соответственно. Тогда наше число t принимает значения: π/2 +2π •k ≤ t ≤ 2π +2π •k, где к – целое число

б)Дуга МK - это дуга с началом в точке М и концом в точке К. Точка М соответственно равна -3π/4, а точка К равна π/4. Значит для точек t имеем: -3π/4 ≤ t ≤ π/4. Но согласно формуле на слайде 8 числам -3π/4 и π/4 соответствуют числа вида -3π/4+2π •k и π/4+2π •k, соответственно. Тогда наше число t принимает значения: -3π/4 +2π •k ≤ t ≤ π/4 +2π •k, где к – целое число