на себя, сохраняющее расстояния.
Виды движения:
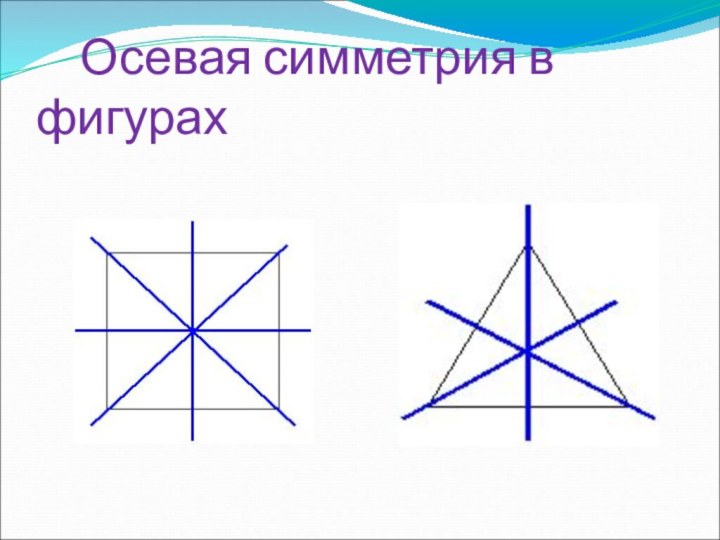
1. Симметрия:
─
осевая,─ центральная,
─ зеркальная.
─ скользящая.
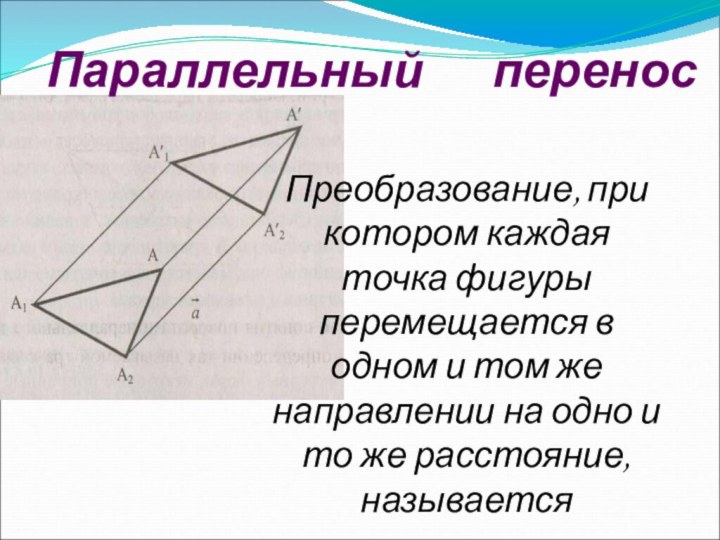
2. Параллельный перенос:
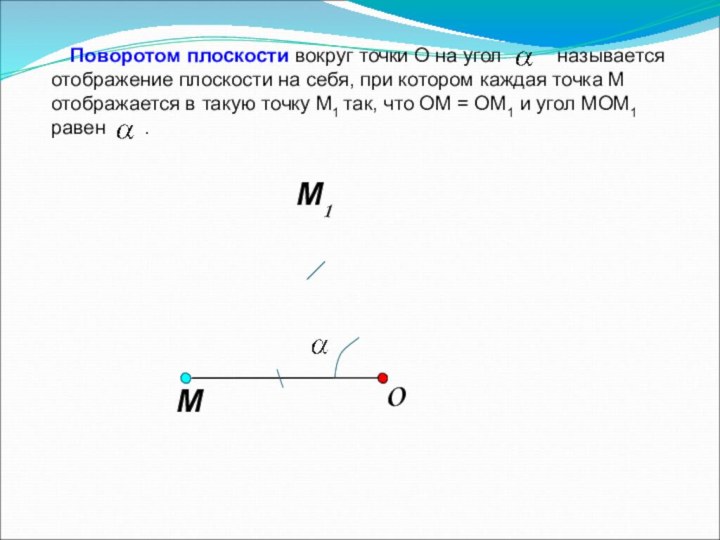
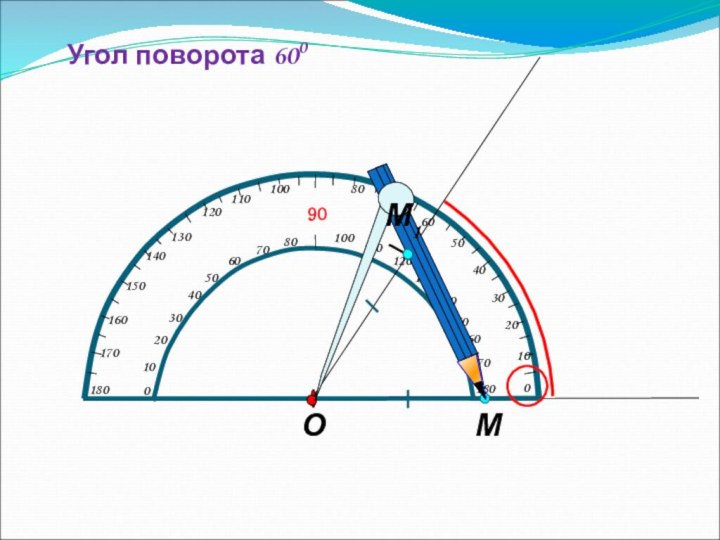
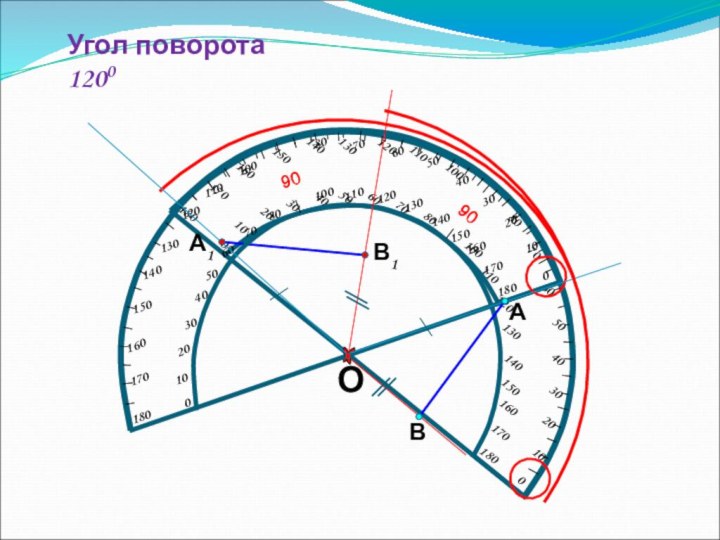
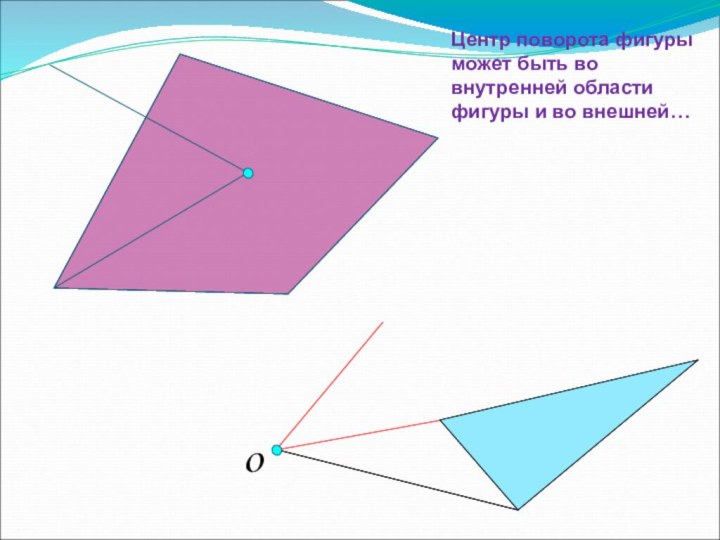
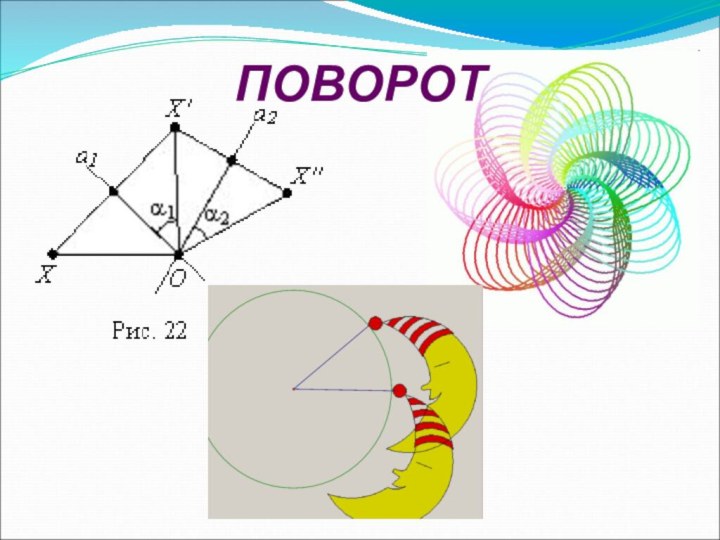
3. Поворот.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






















М
М1