Слайд 2
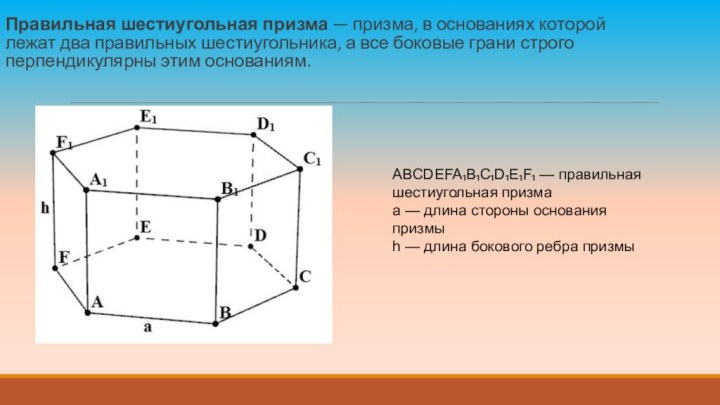
Правильная шестиугольная призма — призма, в основаниях которой лежат
два правильных шестиугольника, а все боковые грани строго перпендикулярны
этим основаниям.
ABCDEFA₁B₁C₁D₁E₁F₁ — правильная шестиугольная призма
a — длина стороны основания призмы
h — длина бокового ребра призмы
Слайд 3
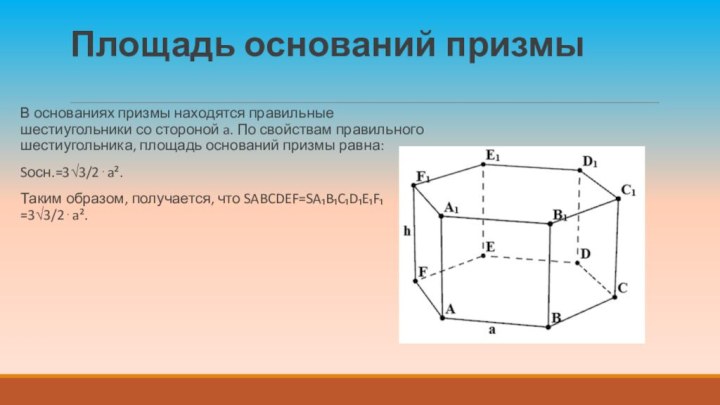
Площадь оснований призмы
В основаниях призмы находятся правильные шестиугольники
со стороной a. По свойствам правильного шестиугольника, площадь оснований
призмы равна:
Sосн.=3√3/2⋅a².
Таким образом, получается, что SABCDEF=SA₁B₁C₁D₁E₁F₁ =3√3/2⋅a².
Слайд 4
Площадь полной поверхности призмы
Площадь полной поверхности призмы складывается
из площадей боковых граней призмы и площадей ее оснований.
Каждая из боковых граней призмы является прямоугольником со сторонами a и h. Следовательно, по свойствам прямоугольника
Sбок.=a⋅h
У призмы шесть боковых граней и два основания, следовательно, площадь ее полной поверхности равна
Sполн.=6⋅Sбок.+2⋅Sосн.=6⋅a⋅h+2⋅3√3/2⋅a².
Слайд 5
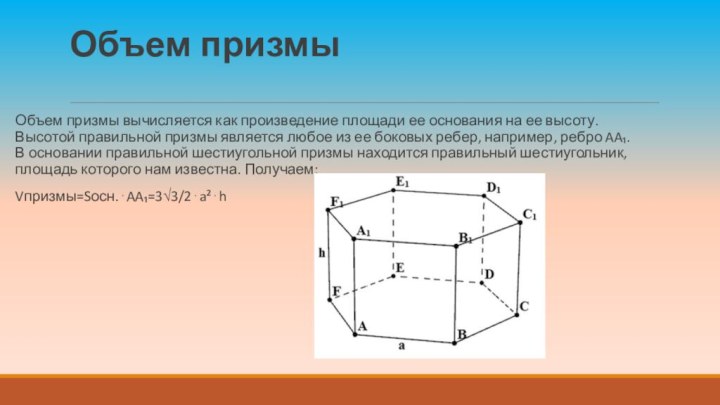
Объем призмы
Объем призмы вычисляется как произведение площади ее
основания на ее высоту. Высотой правильной призмы является любое
из ее боковых ребер, например, ребро AA₁. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем:
Vпризмы=Sосн.⋅AA₁=3√3/2⋅a²⋅h
Слайд 6
Правильный шестиугольник в основаниях призмы
Рассматриваем правильный шестиугольник ABCDEF,
лежащий в основании призмы. Проводим отрезки AD, BE и
CF. Пусть пересечением этих отрезков является точка O. По свойствам правильного шестиугольника, треугольники AOB, BOC, COD, DOE, EOF, FOA являются правильными треугольниками. Отсюда следует, что
AO=OD=EO=OB=CO=OF=a
Проводим отрезок AE, пересекающийся с отрезком CF в точке M. Треугольник AEO равнобедренный, в нём AO=OE=a, ∠EOA=120∘. По свойствам равнобедренного треугольника
AE=a⋅√2(1−cosEOA)=√3⋅a
Аналогичным образом приходим к заключению, что AC=CE=√3⋅a, FM=MO=1/2⋅a.
Слайд 7
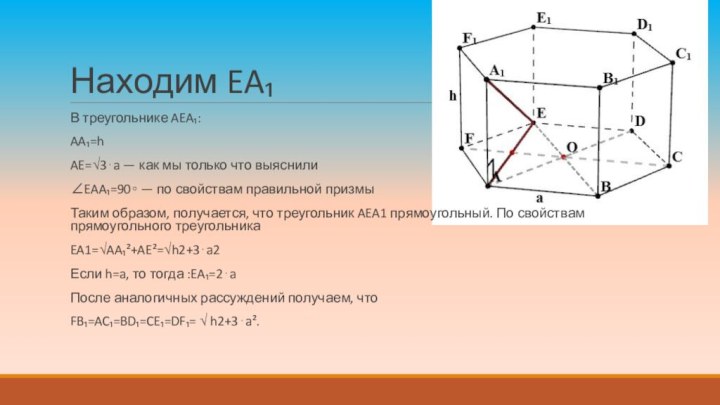
Находим EA₁
В треугольнике AEA₁:
AA₁=h
AE=√3⋅a — как мы только
что выяснили
∠EAA₁=90∘ — по свойствам правильной призмы
Таким образом, получается,
что треугольник AEA1 прямоугольный. По свойствам прямоугольного треугольника
EA1=√AA₁²+AE²=√h2+3⋅a2
Если h=a, то тогда :EA₁=2⋅a
После аналогичных рассуждений получаем, что
FB₁=AC₁=BD₁=CE₁=DF₁= √ h2+3⋅a².
Слайд 8
Находим EB₁
В треугольнике BEB₁:
BB₁=h
BE=2⋅a — потому что EO=OB=a
∠EBB₁=90∘
— по свойствам правильной призмы
Таким образом, получается, что треугольник
BEB1 прямоугольный. По свойствам прямоугольного треугольника
EB1= √BB₁²+BE²=√h²+4⋅a2
Если h=a, то тогда EB₁=√5⋅a
После аналогичных рассуждений получаем, что FC₁=AD₁=BE₁=CF₁=DA₁=√h²+4⋅a².
Слайд 9
Находим OF₁
В треугольнике FOF₁:
FF₁=h
FO=a
∠OFF₁=90∘ — по свойствам правильной
призмы
Таким образом, получается, что треугольник FOF1 прямоугольный. По свойствам
прямоугольного треугольника
OF₁=√FF₁²+OF²=√h²+a²
Если h=a, то тогда OF₁=√2⋅a
После аналогичных рассуждений получаем, что OA₁=OB₁=OC₁=OD₁=OE₁=√h²+a².
Слайд 10
Находим FE₁
В треугольнике FEE₁:
EE₁=h
FE=a
∠FEE₁=90∘ — по свойствам правильной
призмы
Таким образом, получается, что треугольник FEE₁ прямоугольный. По свойствам
прямоугольного треугольника
FE₁=√FE²+EE₁²=√h²+a²
Если h=a, то тогда
FE₁=√2⋅a
После аналогичных рассуждений получаем, что длины диагоналей остальных боковых граней призмы также равны √h²+a².
Слайд 11
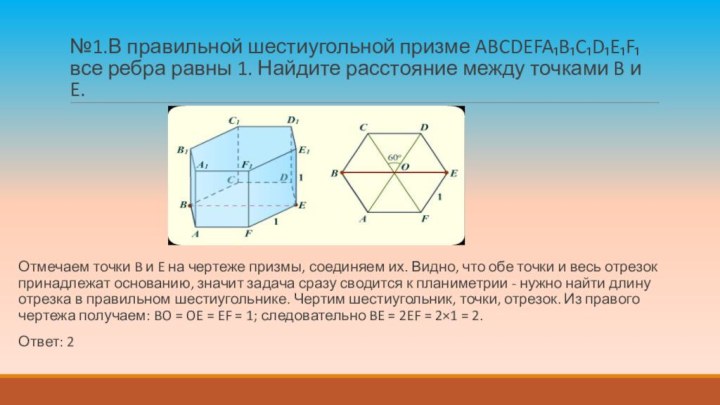
№1.В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны
1. Найдите расстояние между точками B и E.
Отмечаем точки
B и E на чертеже призмы, соединяем их. Видно, что обе точки и весь отрезок принадлежат основанию, значит задача сразу сводится к планиметрии - нужно найти длину отрезка в правильном шестиугольнике. Чертим шестиугольник, точки, отрезок. Из правого чертежа получаем: BO = OE = EF = 1; следовательно BE = 2EF = 2×1 = 2.
Ответ: 2
Слайд 12
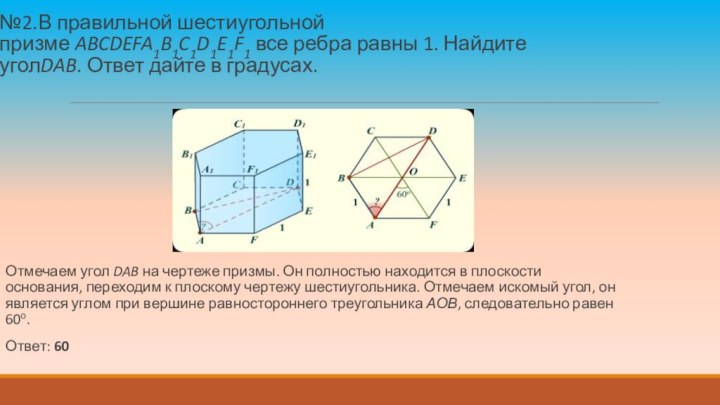
№2.В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите
уголDAB. Ответ дайте в градусах.
Отмечаем угол DAB на чертеже призмы. Он
полностью находится в плоскости основания, переходим к плоскому чертежу шестиугольника. Отмечаем искомый угол, он является углом при вершине равностороннего треугольника АОВ, следовательно равен 60о.
Ответ: 60
Слайд 13
№3.В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите
уголAC1C. Ответ дайте в градусах.
Отмечаем угол AC1C на чертеже призмы. Треугольник AC1C,
содержащий искомый угол, также включает боковое ребро призмы и отрезок, лежащий в её основании, следовательно он прямоугольный (боковое ребро прямой призмы перпендикулярно основанию)
Слайд 14
По условию все ребра равны 1, значит C1C = 1.
Чтобы найти угол прямоугольного треугольника через синус, нам еще
понадобится длина гипотенузы AC1, а чтобы найти угол через тангенс понадобится длина катета AC. Катет AC является отрезком внутри правильного шестиугольника, поэтому его длину найти легче, чем длину диагонали призмы AC1, выбираем способ "через тангенс".
AC находим как основание равнобедренного треугольника АВС с известными боковыми сторонами и углом при вершине 120о. См. самый правый чертеж.
Получим AC = 2·BC·cos30o = 2·1·√3/2 = √3.
Тогда tg∠AC1C = AC/CC1 = √3/1 = √3. Это табличное значение тангенса. Вспоминаем, что ему соответствует угол 60o.
Ответ: 60
Слайд 15
№4.В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны √5. Найдите
расстояние между точками B и E1.
Отмечаем точки B и E1 на чертеже призмы, соединяем их. Видно,
что точки принадлежат разным граням, т.е. отрезок BE1 является диагональю призмы. Соединим также точки В и Е, чтобы построить прямоугольный треугольник BЕE1, который представлен на чертеже справа.
Слайд 16
Угол BЕE1 - прямой. Убедимся в этом: призма прямая, значит
ребро ЕE1 перпендикулярно плоскости основания, значит ЕE1 перпендикулярно любой прямой в этой плоскости,
в том числе BE. Гипотенузу BE1 можно найти по теореме Пифагора, так как катет ЕE1 = √5 по условию задачи, а катет ВЕ легко найти пользуясь свойствами шестиугольника. Мы как раз это делали в предыдущей задаче и получили ВЕ = 2EF = 2·√5.
BE12 = EE12 + BE2 = (√5)2 + (2·√5)2 = 5 + 4·5 = 25;
BE1 = 5.
Ответ: 5
Слайд 17
№5.Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона
основания которой равна 5, а высота – 10.
Решение.
Площадь боковой
поверхности призмы равна сумме площадей всех ее боковых граней:
Sбок=6Sгр
Sгр=ah
Sбок=6·5·10
Ответ: 300.
Слайд 18
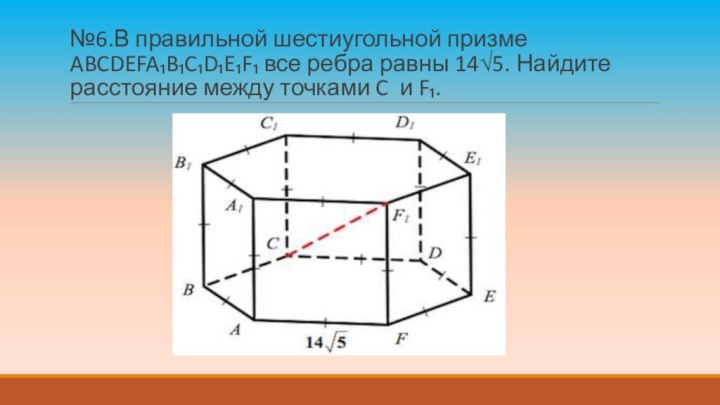
№6.В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны
14√5. Найдите расстояние между точками C и F₁.
Слайд 19
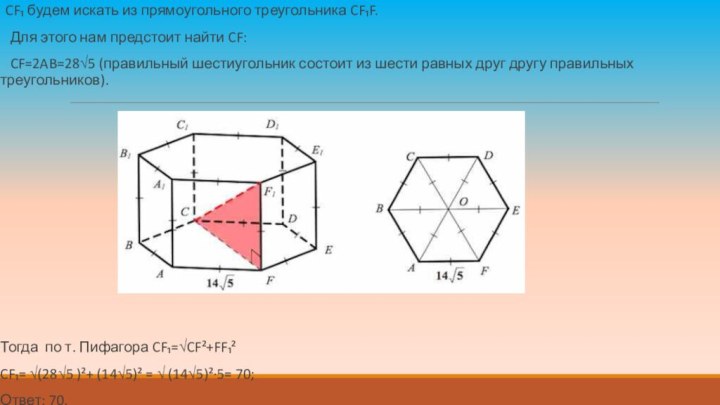
CF₁ будем искать из прямоугольного треугольника CF₁F.
Для этого нам предстоит найти CF:
CF=2AB=28√5 (правильный
шестиугольник состоит из шести равных друг другу правильных треугольников).
Тогда по т. Пифагора CF₁=√CF²+FF₁²
CF₁= √(28√5 )²+ (14√5)² = √ (14√5)²·5= 70;
Ответ: 70.