Презентация на тему Объем прямой призмы

Содержание

2. Теорема: объем прямой призмы равен произведению площади основания на высоту.
3. Доказательство
4. 1. Рассмотрим прямую треугольную призму АВСА1В1С1 С
5. 2. Докажем теорему для произвольной прямой призмы
6. ТЕОРЕМА ДОКАЗАНА.
7. Скачать презентацию
8. Похожие презентации

Теорема: объем прямой призмы равен произведению площади основания на высоту.

1. Рассмотрим прямую треугольную призму АВСА1В1С1 С ОБЪЕМОМ V и высотой h.

2. Докажем теорему для произвольной прямой призмы с высотой h и площадью

Работу выполнила: ученица 11 «А» класса Смотраева Наталья Работу проверила: Хайбрахманова Г.Ф.

Слайды презентации

Слайд 2 Теорема: объем прямой призмы равен произведению площади основания

на высоту.

Слайд 3 Доказательство

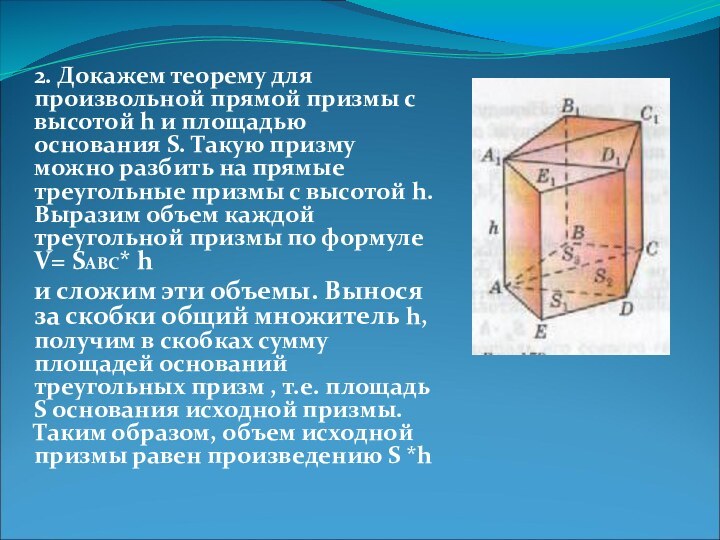
Слайд 4 1. Рассмотрим прямую треугольную призму АВСА1В1С1 С ОБЪЕМОМ

1. Рассмотрим прямую треугольную призму АВСА1В1С1 С ОБЪЕМОМ V и высотой

V и высотой h. Проведем такую высоту треугольника АВС,

которая разделяет этот треугольник на два треугольника. Плоскость ВВ1 Д разделяет данную призму на две призмы, основаниями которых являются прямоугольные треугольники АВД и ВДС. Поэтому объемы V1 и V2 этих призм соответственно равны SАВД* h и SВДС* h . Таким образом V= SАВС* h

Слайд 5 2. Докажем теорему для произвольной прямой призмы с

2. Докажем теорему для произвольной прямой призмы с высотой h и

высотой h и площадью основания S. Такую призму можно

разбить на прямые треугольные призмы с высотой h. Выразим объем каждой треугольной призмы по формуле V= SАВС* h
и сложим эти объемы. Вынося за скобки общий множитель h, получим в скобках сумму площадей оснований треугольных призм , т.е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен произведению S *h