Слайд 2
9 класс
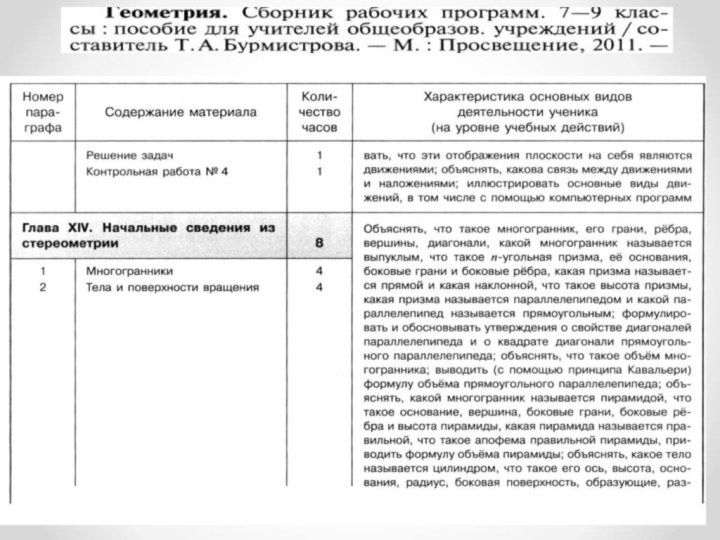
6. Начальные сведения из стереометрии
Предмет стереометрии. Геометрические
тела и поверхности. Многогранники: призма, параллелепипед, пирамида, формулы для
вычисления их объемов. Тела и поверхности вращения: цилиндр, конус, сфера, шар, формулы для вычисления их площадей поверхностей и объемов.
Основная цель — дать начальное представление о телах и поверхностях в пространстве: познакомить учащихся с основными формулами для вычисления площадей поверхностей и объемов тел.
Рассмотрение простейших многогранников (призмы, параллелепипеда, пирамиды), а также тел и поверхностей вращения (цилиндра, конуса, сферы, шара) проводится на основе наглядных представлений, без привлечения аксиом стереометрии. Формулы для вычисления объемов указанных тел выводятся на основе принципа Кавальери, формулы для вычисления площадей боковых поверхностей цилиндра и конуса получаются с помощью разверток этих поверхностей, формула площади сферы приводится без обоснования.
Слайд 3
Планируемые результаты
по теме «Многогранник и его элементы
Начальные

сведения из стереометрии
ЗНАТЬ: что такое многогранник, его грани,
ребра, вершины, диагонали.
Какой многогранник называется выпуклы.
Что такое n-угольная призма, ее основания, боковые грани и боковые ребра.
Какая призма называется прямой, и какая наклонной, что такое высота призмы, какая призма называется параллелепипедом и какой параллелепипед называется прямоугольным.
утверждения о свойстве диагоналей параллелепипеда и квадрате диагонали прямоугольного параллелепипеда.
объем многогранника.
.Какой многогранник называется пирамидой, что такое основание, вершина, боковые грани, боковые ребра, и высота пирамиды.
Какая пирамида называется правильной, что такое апофема правильной пирамиды.
Знать формулу объема пирамиды.
какое тело называется цилиндром.
Знать, что такое его ось, высота, основания, радиус, боковая поверхность, образующие, развертка боковой поверхности.
формулами объем и площадь боковой поверхности цилиндра.
какое тело называется конусом
формулами объем и площадь боковой поверхности конуса
, какая поверхность называется сферой и какое тело называется шаром.
Что такое радиус и диаметр сферы(шара).
УМЕТЬ: Выводить( с помощью принципа Кавальери) формулу объема прямоугольного параллелепипедаКакими формулами выражаются объем шара и площадь сферы.
Изображать и распознавать на рисунках призму, параллелепипед, пирамиду, цилиндр, конус, шар.
Слайд 5
Календарно-тематический план 9 класс
Слайд 6
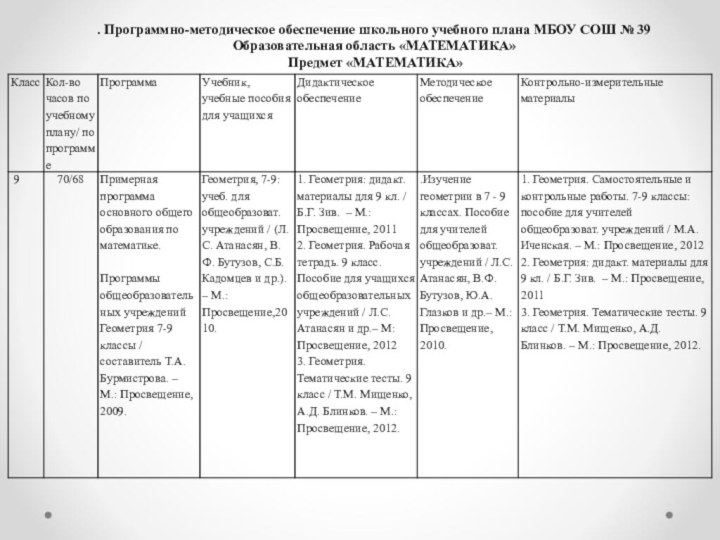
. Программно-методическое обеспечение школьного учебного плана МБОУ СОШ
№ 39
Образовательная область «МАТЕМАТИКА»
Предмет «МАТЕМАТИКА»
Слайд 7
Геометрия. Методические рекомендации. 9 класс :учеб. пособие для
общеобразоват. организаций /[Л. С. Атанасян, В. Ф. Бутузов, Ю.
А. Глазков и
др.]. — М. : Просвещение, 2015.
Г Л А В А ХIV Начальные сведения из стереометрии (2 ч)
При наличии времени учитель может ознакомить учащихся с некоторыми пространственными фигурами — многогранниками, а также телами и поверхностями вращения, построив свой рассказ в виде лекции по материалам главы XIV. Можно предложить наиболее сильным учащимся самим разобрать решение задачи 1188 на построение сечения параллелепипеда и решить аналогичные задачи 1189—1192.
При необходимости отведённые на знакомство с элементами стереометрии 2 урока можно использовать как дополнительные уроки повторения и подготовки к ГИА.
Слайд 8
10 класс
4. Многогранники
Понятие многогранника. Призма. Пирамида. Правильные многогранники.
Основнаяцель—
познакомить учащихся с основными видами многогранников (призма, пирамида, усеченная
пирамида), с формулой Эйлера для выпуклых многогранников, с правильными многогранниками и элементами их симметрии.
С двумя видами многогранников — тетраэдром и параллелепипедом — учащиеся уже знакомы. Теперь эти представления расширяются. Многогранник определяется как поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело (его тоже называют многогранником). В связи с этим уточняется само понятие геометрического тела, для чего вводится еще ряд новых понятий (граничная точка фигуры, внутренняя точка и т. д.). Усвоение их не является обязательным для всех учащихся, можно ограничиться наглядным представлением о многогранниках.
Слайд 9
Изучение геометрии в 10 классе по теме: «Многогранники»
направлено на решение следующих задач:
Сформировать представление о геометрических телах
и их поверхностях, об изображении пространственных фигур на чертеже;
Изучить свойства прямоугольного параллелепипеда;
Сформировать представления об основных видах многогранников.
Слайд 10
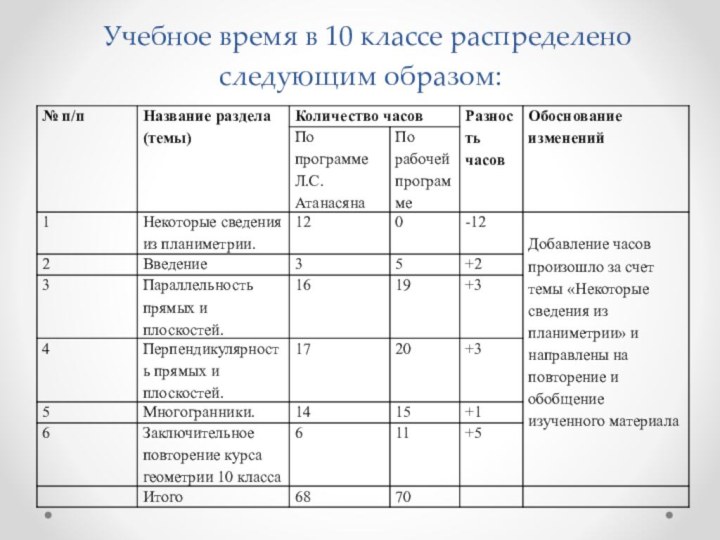
Учебное время в 10 классе распределено следующим
образом:
Слайд 11
Геометрия
Планиметрия
Стереометрия
stereos
телесный, твердый, объемный, пространственный
Слайд 12
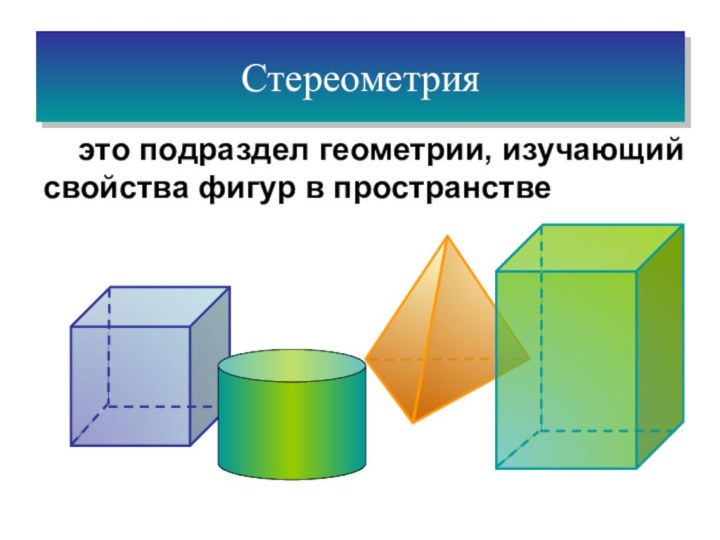
это подраздел геометрии, изучающий свойства фигур в пространстве
Стереометрия
Слайд 13
1. Многогранники.Теория:
Часть геометрии, изучаемую до сих пор, называется планиметрией — эта

часть была о свойствах плоских геометрических фигур, то есть фигур,
целиком расположенных в некоторой плоскости. Но окружающие нас предметы в большинстве не являются плоскими. Любой реальный предмет занимает какую-то часть пространства.
Раздел геометрии, в котором изучаются свойства фигур в пространстве, называется стереометрией.
Это слово στερεομετρία происходит от древнегреческих слов «stereos» — объёмный, пространственный и «metria» — измерение.
Простейшие фигуры стереометрии — точки, прямые и плоскости. Из этих фигур образованы геометрические тела и их поверхности. Если поверхности геометрических тел составлены из многоугольников, то такие тела называются многогранниками.
Многоугольники, из которых составлен многогранник, называются его гранями. При этом предполагается, что никакие две соседние грани многогранника не лежат в одной плоскости
Стороны граней называются рёбрами, а концы рёбер — вершинами многогранника.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Слайд 14
Многогранники бывают выпуклыми и невыпуклыми.
Выпуклый многогранник характеризуется тем, что он расположен
по одну сторону от плоскости каждой своей грани
. На
рисунке выпуклый многогранник — октаэдр. У октаэдра восемь граней, все грани — правильные треугольники.
На рисунке — невыпуклый (вогнутый) многоугольник. Если рассмотреть, например, плоскость треугольника EDC ,
то, очевидно, часть многоугольника находится по одну сторону, а часть по другую сторону этой плоскости.
Слайд 15
Призма
Теперь можем ввести определение призмы.
n -угольной призмой называют
многогранник, составленный из двух равных n -угольников, лежащих в параллельных
плоскостях, и n -параллелограммов, которые образовались при соединении вершин n -угольников отрезками
параллельных прямых.
Равные n -угольники называют основаниями призмы.
Стороны многоугольников называют рёбрами оснований.
Параллелограммы называют боковыми гранями призмы.
Параллельные отрезки называют боковыми рёбрами призмы.
Призмы бывают прямыми и наклонными.
Если основания прямой призмы — правильные многоугольники, то такую призму называют правильной.
У прямых призм все боковые грани — прямоугольники. Боковые ребра прямой призмы перпендикулярны к плоскостям её оснований.
Если из любой точки одного основания провести перпендикуляр к другому основанию призмы, то этот перпендикуляр называют высотой призмы.
На рисунке наклонная четырёхугольная призма,
в которой проведена высота B 1 E .
Слайд 16
В прямой призме каждое из боковых рёбер является
высотой призмы.
На рисунке прямая треугольная призма. Все боковые грани
— прямоугольники, любое боковое ребро
можно называть высотой призмы. У треугольной призмы нет диагоналей, так как все вершины соединены рёбрами.
На рисунке — правильная четырёхугольная призма. Основания призмы — квадраты. Все диагонали правильной
четырёхугольной призмы равны, пересекаются в одной точке и делятся в этой точке пополам.
Четырёхугольная призма, основания которой — параллелограммы, называется параллелепипедом.
Слайд 17
Правильную четырёхугольную призму можно также называть прямым параллелепипедом.
Если
основания прямого параллелепипеда — прямоугольники, то этот параллелепипед
—
прямоугольный.
На рисунке — прямоугольный параллелепипед. Длины трёх рёбер с общей вершиной
называют измерениями прямоугольного параллелепипеда.
Например, AB , AD и AA 1 можно называть измерениями.
Так как треугольники ABC и ACC 1 — прямоугольные, то, следовательно,
квадрат длины диагонали прямоугольного параллелепипеда равен сумме
квадратов его измерений: AC 1 2 =AB 2 +AD 2 +AA 1 2
Слайд 18
Основные формулы для расчётов в прямых призмах
1. Боковая
поверхность S бок. =P осн. ⋅H , где H — высота призмы. Для наклонных
призм площадь каждой боковой грани определяется отдельно.
2. Полная поверхность S полн. =2⋅S осн. +S бок. . Эта формула справедлива для всех призм, не только для прямых.
3. Объём V=S осн. ⋅H . Эта формула справедлива для всех призм, не только для прямых.
Если через соответственные диагонали оснований провести сечение, то его называют
диагональным сечением призмы.
В прямых призмах диагональные сечения являются прямоугольниками.
Через равные диагонали проходят равные диагональные сечения.
На рисунке — правильная шестиугольная призма, в которой проведены два разные
диагональных сечения, которые проходят через диагонали с разными длинами.
Слайд 19
Пирамида
n -угольная пирамида — многогранник, составленный из n -угольника
в основании и n -треугольников
, которые образовались при соединении точки вершины
пирамиды со всеми вершинами многоугольника
основания.n -угольник называют основанием пирамиды.
Треугольники — боковые грани пирамиды.
Общая вершина треугольников — вершина пирамиды.
Рёбра, выходящие из вершины — боковые ребра пирамиды.
Перпендикуляр от вершины пирамиды к плоскости основания называют высотой пирамиды.
На рисунке шестиугольная пирамида GABCDEF , проведена высота пирамиды GH .
Пирамиду, в основании которой правильный многоугольник и высота соединяет вершину пирамиды с центром
правильного многоугольника, называют правильной.
У правильной пирамиды все боковые грани — равные равнобедренные треугольники. Если провести высоты этих
треугольников, то они также будут равны.
Высоту боковой грани правильной пирамиды называют апофемой.
На рисунке проведено диагональное сечение правильной четырёхугольной пирамиды.
Слайд 20
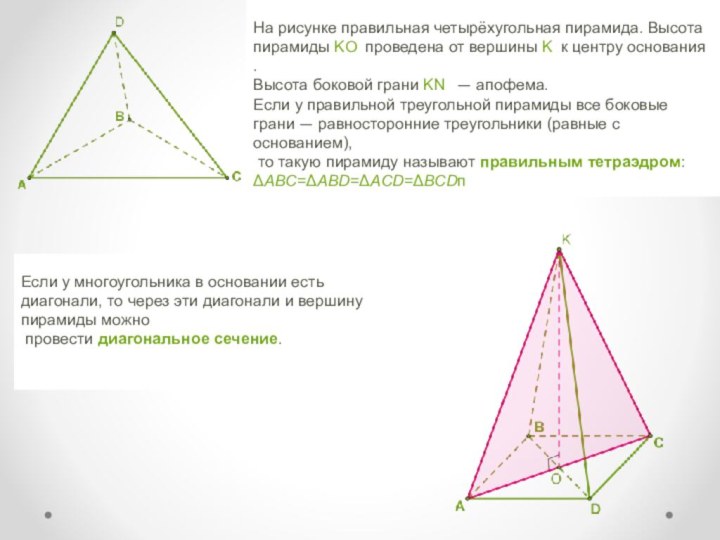
На рисунке правильная четырёхугольная пирамида. Высота пирамиды KO
проведена от вершины K к центру основания .
Высота боковой
грани KN — апофема.
Если у правильной треугольной пирамиды все боковые грани — равносторонние треугольники (равные с основанием),
то такую пирамиду называют правильным тетраэдром:
ΔABC=ΔABD=ΔACD=ΔBCDп
Если у многоугольника в основании есть диагонали, то через эти диагонали и вершину пирамиды можно
провести диагональное сечение.
Слайд 21
Основные формулы для расчётов в правильных пирамидах
1. Боковая
поверхность S бок. =P осн. ⋅h2 , где h — апофема. Для пирамид,
которые не являются правильными, необходимо определить отдельно поверхность каждой боковой грани.
2. Полная поверхность S полн. =S осн. +S бок. . Эта формула справедлива для всех пирамид, не только для правильных.
3. Объём V=13 ⋅S осн. ⋅H , где H — высота пирамиды. Эта формула справедлива для всех пирамид, не только для правильных.
Слайд 22
Тела и поверхности вращения
Цилиндр
Цилиндр можно получить вращением прямоугольника AA1O1O вокруг
одной из его сторон OO1
или прямоугольника AA1B1B вокруг прямой OO1, которая проходит через
серединные точки противолежащих сторон.
Прямая OO1 называется осью цилиндра, AA1 и BB1 — образующими.
Высота H цилиндра совпадает с любым из отрезков OO1=AA1=BB1.
Два круга, которые образовались при вращении, называют основаниями цилиндра.
Радиусом R=OA=OB цилиндра называется радиус его основания.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось.
Осевым сечением цилиндра (прямого кругового цилиндра) является прямоугольник, на данном рисунке — прямоугольникAA1B1B.
Слайд 23
Развёртка боковой поверхности цилиндра тоже прямоугольник:
Боковая поверхность прямого
кругового цилиндра равна произведению длины окружности
основания на высоту:
Sбок.=2πRH
Полная
поверхность цилиндра вычисляется по формуле:
S=Sбок.+2Sосн.=2πRH+2πR2
Для объёма прямого кругового цилиндра верно:
V=πR2H
Слайд 24
Конус
Конус можно получить вращением прямоугольного треугольника POA вокруг
одного из его
катетов PO
или равнобедренного треугольника APB вокруг прямой PO, проходящей через
вершину P и середину O
основания треугольника.
Осью прямого кругового конуса называется прямая PO, содержащая его высоту H.
Осевое сечение конуса, проходящее через его вершину, представляет собой
равнобедренный треугольник,
у которого боковые стороны PA и PB являются образующими l конуса.
Радиус конуса R=OA=OB — это радиус основания.
Слайд 25
Развёртка боковой поверхности конуса представляет
собой круговой сектор:
Радиус этого
сектора равен образующей конуса, то есть равен l, а длина дуги сектора равна длине окружности основания конуса, то есть равна 2πr.
Площадь боковой поверхности конуса определяется как площадь данного кругового сектора:
Sбок.=πl2⋅α°360°
Если рассмотреть длину окружности основания конуса как длину дуги кругового сектора, получаем:
2πR=2πl⋅α°360°2πR=πl⋅α°180°α°=2πR⋅180°πl=R⋅360°lSбок.=πl2⋅α°360°=πl2⋅R⋅360°360°⋅l=πRl
Sбок.=πRl — ещё одна формула для определения боковой поверхности конуса.
Полная поверхность конуса:
S=Sбок.+Sосн.=πRl+πR2
Объём конуса находим по формуле:
V=13πR2H
Слайд 26
Шар и поверхность шара — сфера
Сфера получается при вращении
полукруга или круга вокруг его диаметра AB как оси.
Граница шара
называется шаровой поверхностью или сферой.
Таким образом, точками сферы являются все точки шара, которые удалены от центра O на расстояние, равное радиусу R.
Любой отрезок, как OA, OB и OC или другие, соединяющие центр шара с точкой шаровой поверхности,
также называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром,
как AB на рисунке. Концы любого диаметра называются диаметрально противоположными точками шара.
Сечение шара плоскостью, проходящей через его центр,
называется большим кругом, а сечение сферы —
большой окружностью.
Поверхность сферы:
S=4πR2
Объём шара:
V=43πR3
Слайд 28
Стереометрией
называется раздел геометрии, в котором изучаются свойства
фигур в пространстве.
«стерео» - объёмный,пространственный;
«метрео» - измерять
Слайд 29
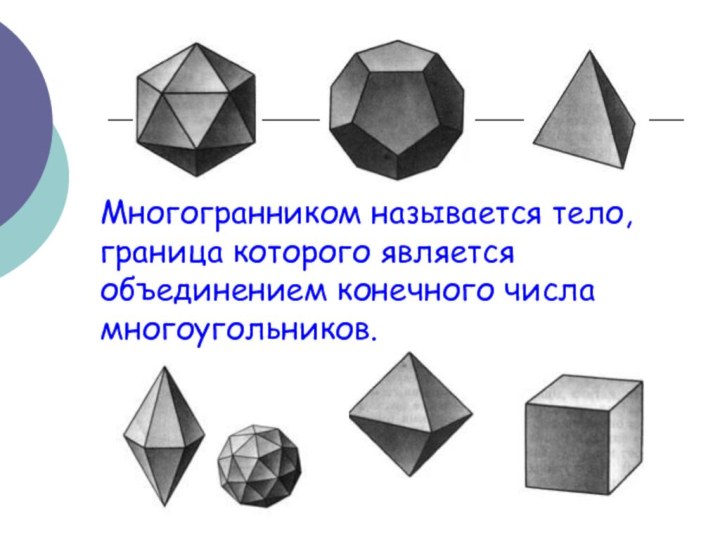
Многогранником называется тело, граница которого является объединением конечного
числа многоугольников.
Слайд 30
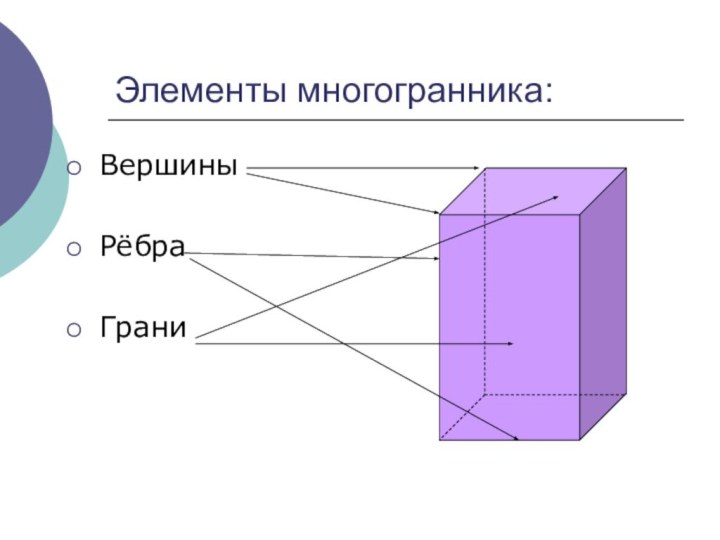
Элементы многогранника:
Вершины
Рёбра
Грани
Слайд 31
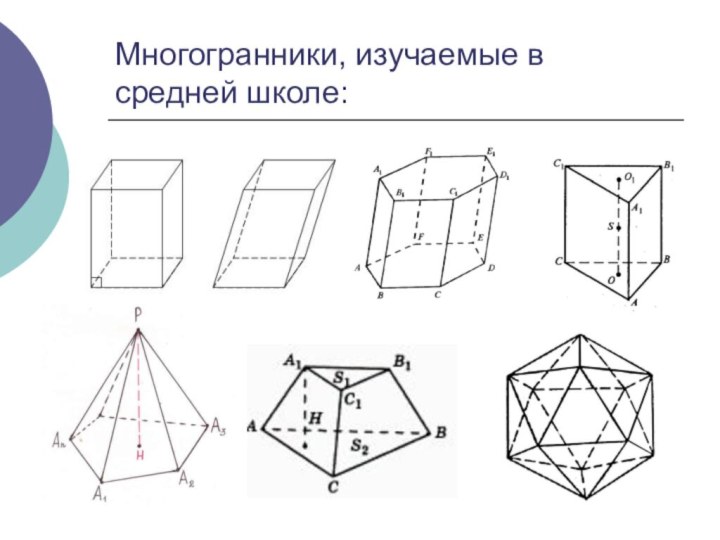
Многогранники, изучаемые в средней школе:
Слайд 32
Многогранники
выпуклые
невыпуклые
Тела
Архимеда
Тела
Платона
Тела
Кеплера-
Пуансо
Слайд 33
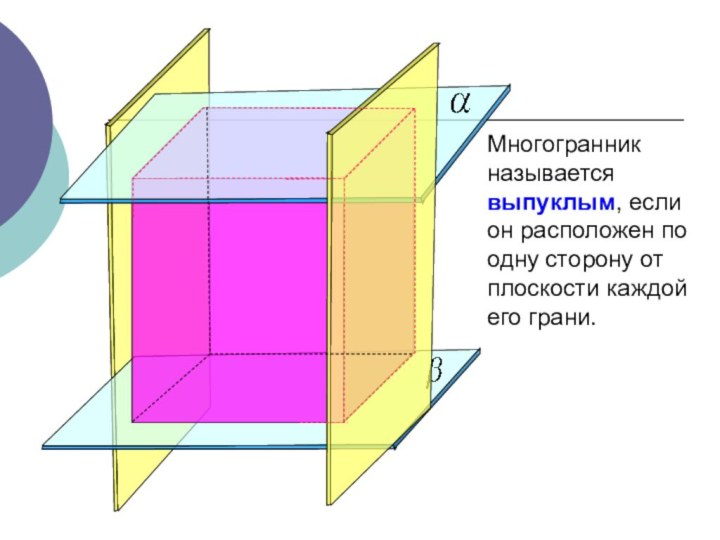
Многогранник называется выпуклым, если он расположен по одну
сторону от плоскости каждой его грани.
Слайд 34
Невыпуклый многогранник – многогранник, расположенный по разные стороны
от плоскости одной из его граней.
Слайд 35
Правильными многогранниками
называют выпуклые многогранники, все грани и
все углы которых равны, причем грани - правильные многоугольники.
Слайд 36
Тетраэдр
Икосаэдр
Гексаэдр
Додекаэдр
Октаэдр
Слайд 37
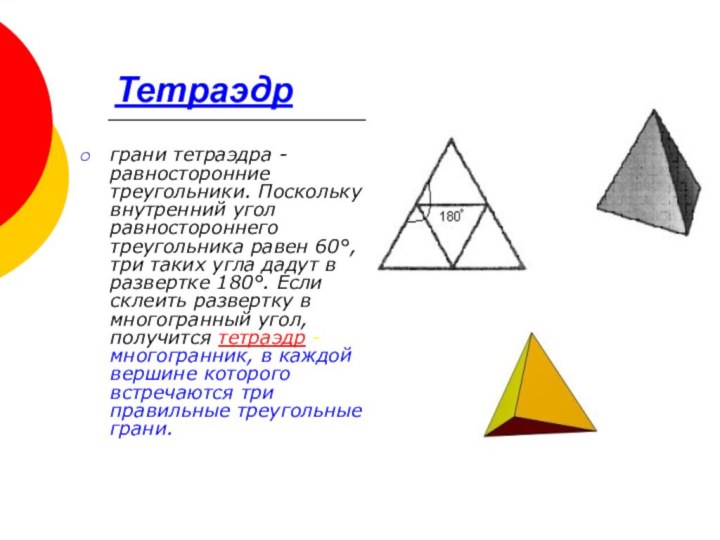
Тетраэдр
грани тетраэдра - равносторонние треугольники. Поскольку внутренний угол
равностороннего треугольника равен 60°, три таких угла дадут в
развертке 180°. Если склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани.
Слайд 38
Октаэдр-
Если добавить к развертке вершины еще один треугольник,
в сумме получится 240°. Это развертка вершины октаэдра. Октаэдр-восьмигранник,
тело, ограниченное восемью правильными треугольниками.
Слайд 39
Икосаэдр
Добавление пятого треугольника даст угол 300° - получаем
развертку вершины икосаэдра.
Икосаэдр-двадцатигранник, тело, ограниченное двадцатью равносторонними треугольниками
Слайд 40
Если же добавить еще один, шестой треугольник, сумма
углов станет равной 360° - эта развертка, очевидно, не
может соответствовать ни одному выпуклому многограннику.
Слайд 41
Куб или правильный гексаэдр
Развертка
из трех квадратных граней имеет угол 3x90°=270° - получается
вершина куба, который также называют гексаэдром. Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник.
Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами.
Слайд 42
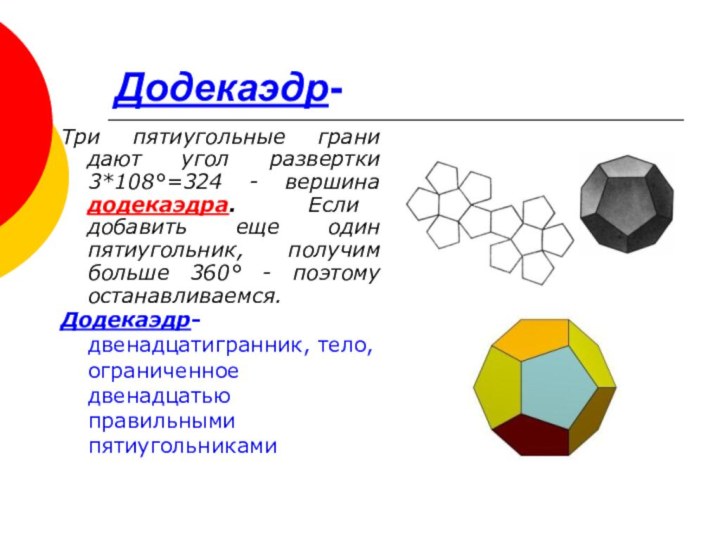
Додекаэдр-
Три пятиугольные грани дают угол развертки 3*108°=324 -
вершина додекаэдра. Если добавить еще один пятиугольник, получим больше
360° - поэтому останавливаемся.
Додекаэдр-двенадцатигранник, тело, ограниченное двенадцатью правильными пятиугольниками
Слайд 43
Для шестиугольников уже три грани дают угол развертки
3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не
существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.
Слайд 44
Вывод:
Существует лишь пять выпуклых правильных многогранников - тетраэдр,
октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с
квадратными гранями и додекаэдр с пятиугольными гранями. Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:
«эдра» - грань
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«додека» - 12
Слайд 45
Тетраэдр
Икосаэдр
Гексаэдр
Додекаэдр
Октаэдр
Слайд 46
Эти тела еще называют телами Платона
Платон связал с
этими телами формы атомов основных стихий природы.
Слайд 47
огонь
тетраэдр
вода
икосаэдр
воздух
октаэдр
земля
гексаэдр
вселенная
додекаэдр
стихии
Слайд 48
Тела Архимеда
Архимедовыми телами называются полуправильные однородные выпуклые многогранники,
то есть выпуклые многогранники, все многогранные углы которых равны,
а грани - правильные многоугольники нескольких типов.
Слайд 50
Тела
Кеплера - Пуансо
Среди невыпуклых однородных многогранников существуют
аналоги платоновых тел - четыре правильных невыпуклых однородных многогранника
или тела Кеплера - Пуансо.
Как следует из их названия, тела Кеплера-Пуансо - это невыпуклые однородные многогранники, все грани которых - одинаковые правильные многоугольники, и все многогранные углы которых равны. Грани при этом могут быть как выпуклыми, так и невыпуклыми.
Слайд 51
Большой звездчатый
додекаэдр
Большой икосаэдр
Малый звездчатый
додекаэдр
Звёздчатый октаэдр
Слайд 52
Многогранники в архитектуре
Великая пирамида в Гизе. Эта грандиозная
Египетская пирамида является древнейшим из Семи чудес древности.
Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц.
Слайд 53
Александрийский маяк.
Маяк был построен на
маленьком острове Фарос в Средиземном море, около берегов Александрии.
Этот оживленный порт основал Александр Великий во время посещения Египта. Сооружение назвали по имени острова. На его строительство ушло 20 лет, а завершен он был около 280 г. до н.э., во времена правления Птолемея II, царя Египта.
Слайд 54
Александрийский (Фаросский) маяк состоял из трех мраморных башен,
стоявших на основании из массивных каменных блоков. Первая башня
была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню.
Слайд 55
Многогранники используются и в современной архитектуре
Слайд 56
В Германии есть памятник правильным многогранникам
Слайд 57
Многогранники в искусстве
Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер
(1471- 1528) , в известной гравюре ''Меланхолия '‘ на
переднем плане изобразил додекаэдр.
Слайд 58
Сальвадор Дали на картине «Тайная вечеря» изобразил
И.
Христа со своими учениками на фоне огромного прозрачного додекаэдра.
Слайд 59
Многогранники в природе
Правильные многогранники – самые выгодные фигуры.
И природа этим широко пользуется. Подтверждением тому служит форма
некоторых кристаллов.
Кристалл сульфата меди II
Кристалл алюмокалиевых
квасцов
Кристалл сульфата никеля II
Слайд 60
Пчёлы
строили свои
шестиугольные соты
задолго до появления человека.
Слайд 61
Домашнее задание
П.118,119,120.
Обратить внимание на материал, о котором не
сказали на уроке.
№ 1184, 1186.