Презентация на тему по математике на тему Теорема Пифагора(8 класс)

геометрии, понимания роли геометрии в решении практических задач, возникающих

в окружающем нас мире.
Воспитание у учащихся общеучебных умений и навыков: работы с дополнительной литературой по математике; поиска, выбора и анализа нужной информации по заданной теме и составления исчерпывающего сообщения в краткой форме; оформления наглядности и защиты своего выступления.
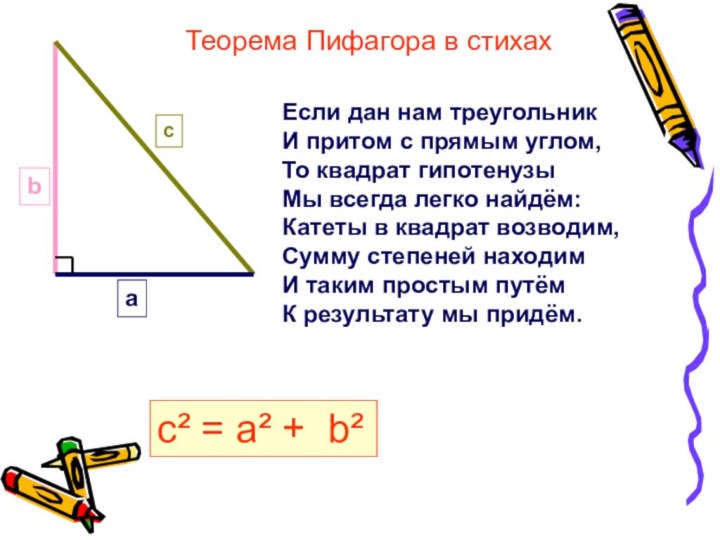
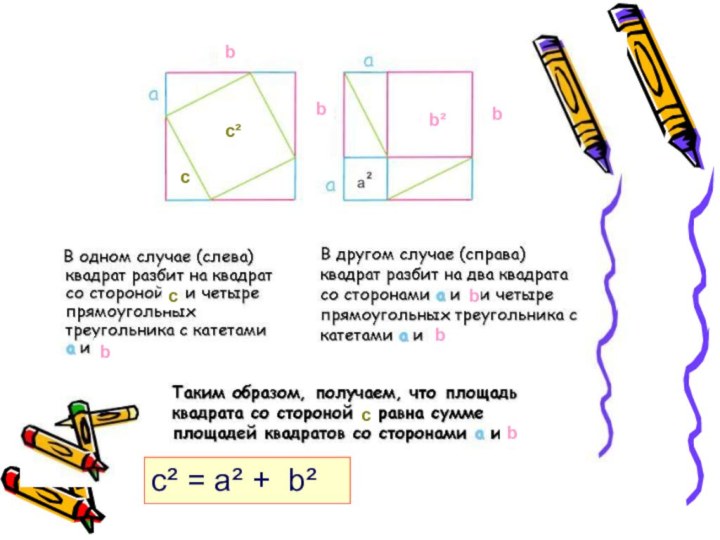
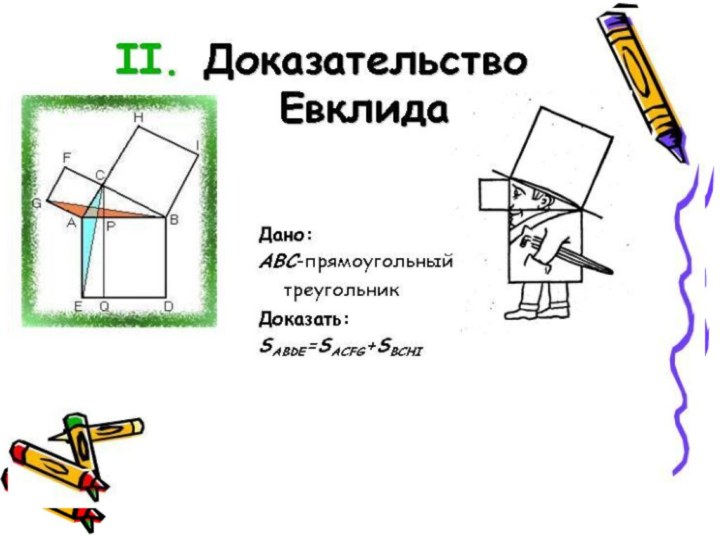
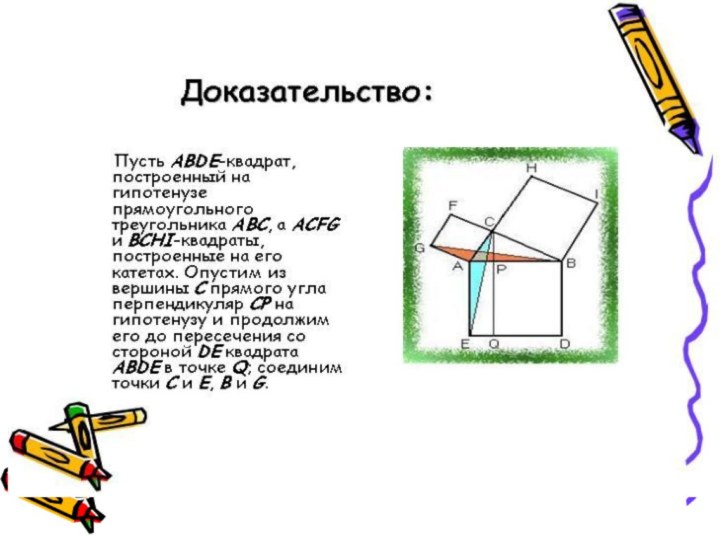
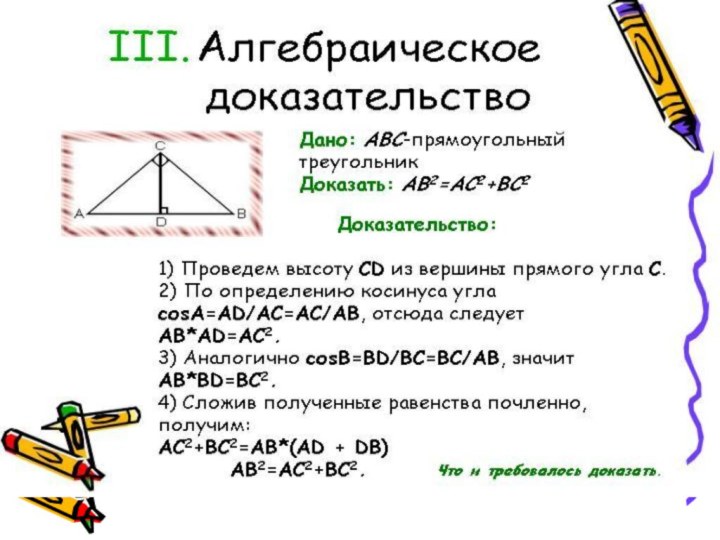
Расширение познания учащихся о жизни великого математика Пифагора, о знаменитой теореме Пифагора и её различных способах доказательства.
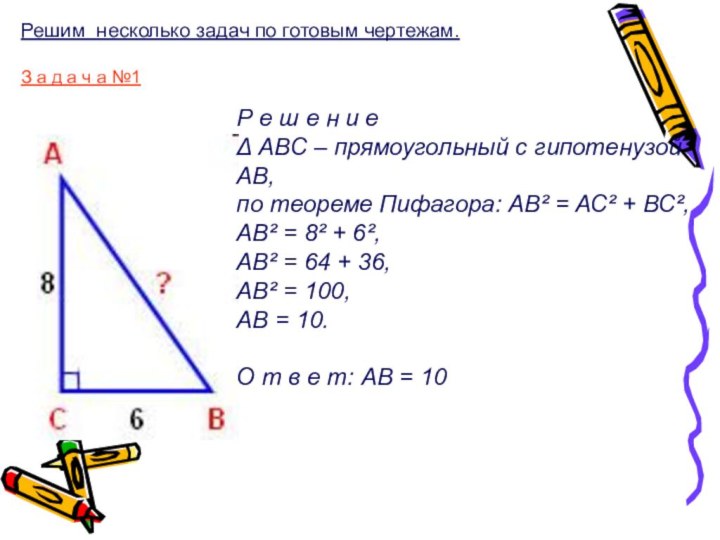
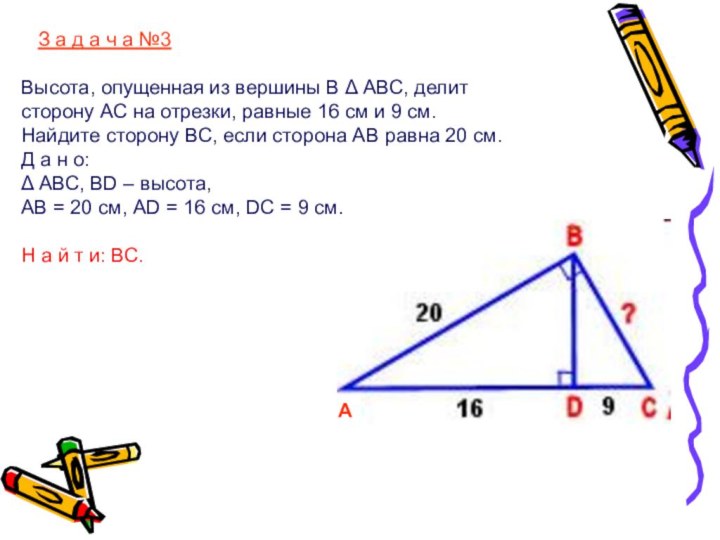
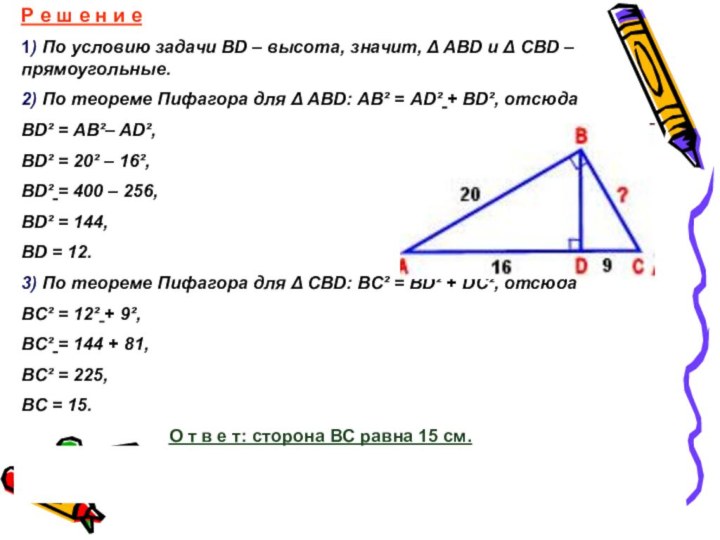
Рассмотрение решения разных практических задач на применение теоремы Пифагора.

Пифагора
Вопросы гостям

квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней

находим
И таким простым путём
К результату мы придём.

c² = a² + b²

Теорема Пифагора в стихах

до н. э.) древнегреческий математик и философ-идеалист. Родился на

острове Самос. Получил хорошее образование. По преданию Пифагор, чтобы ознакомиться с мудростью восточных ученых, выехал в Египет и как будто прожил там 22 года. Хорошо овладев всеми науками египтян, в том числе и математикой, он переехал в Вавилон, где прожил 12 лет и ознакомился с научными знаниями вавилонских жрецов. Предания приписывают Пифагору посещение и Индии. Это очень вероятно, так как Иония и Индия тогда имели торговые связи. Возвратившись на родину (ок. 530 г. до н. э.), Пифагор попытался организовать свою философскую школу. Однако по неизвестным причинам он вскоре оставляет Самос и селится в Кротоне (греческая колония на севере Италии). Здесь Пифагору удалось организовать свою школу, которая действовала почти тридцать лет. Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством.

и, по одной из версий, в возрасте восьмидесяти лет

Пифагор был убит в уличной схватке во время народного восстания.
После его смерти ученики окружили имя своего учителя множеством легенд

Легенда о том, что в честь своего открытия Пифагор принес в жертву быка или, как рассказывают другие, сто быков, послужила поводом для юмора в рассказах писателей и в стихах поэтов. Так, например, немецкий писатель-романист А. Шамиссо, который в начале XIX в. участвовал в кругосветном путешествии на русском корабле "Рюрик", написал следующие стихи:

ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно

было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.

О теореме Пифагора

построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов,

построенных на его катетах". Действительно, с² – площадь квадрата, построенного на гипотенузе, а² и b² – площади квадратов, построенных на катетах.

слов”.

а ч а №1

Р е ш е н

и е
Δ АВС – прямоугольный с гипотенузой АВ,
по теореме Пифагора: АВ² = АС² + ВС²,
АВ² = 8² + 6²,
АВ² = 64 + 36,
АВ² = 100,
АВ = 10.

О т в е т: АВ = 10

е ш е н и е

Δ DCE –

прямоугольный с гипотенузой DE
по теореме Пифагора: DE² = DС² + CE²,
DC² = DE² – CE²,
DC² = 5² – 3²,
DC² = 25 – 9,
DC² = 16,
DC = 4.
О т в е т: DC = 4

Получили прямоугольный треугольник со сторонами 3, 4 и 5 ед. Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен ещё древним египтянам. Они использовали этот треугольник в "правиле верёвки" для построения прямых углов при закладке зданий, храмов, алтарей… Об этом вы прочитаете дома.

опущенная из вершины В Δ АВС, делит сторону АС

на отрезки, равные 16 см и 9 см.
Найдите сторону ВС, если сторона АВ равна 20 см.
Д а н о:
Δ АВС, BD – высота,
АВ = 20 см, AD = 16 см, DC = 9 см.

Н а й т и: ВС.

А

По условию задачи BD – высота, значит, Δ ABD

и Δ CBD – прямоугольные.
2) По теореме Пифагора для Δ ABD: АВ² = AD² + BD², отсюда
BD² = AB²– AD²,
BD² = 20² – 16²,
BD² = 400 – 256,
BD² = 144,
BD = 12.
3) По теореме Пифагора для Δ СBD: ВС² = ВD² + DС², отсюда
BC² = 12² + 9²,
BC² = 144 + 81,
BC² = 225,
BC = 15.
О т в е т: сторона BC равна 15 см.

П и ф а г о р а

Суть

истины вся в том, что нам она – навечно,
Когда хоть раз в прозрении её увидим свет,
И теорема Пифагора через столько лет
Для нас. Как для него, бесспорна, безупречна …

(Отрывок из стихотворения А. Шамиссо)

мачты нужно установить 4 троса. Один конец каждого троса

должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты.
Хватит ли 50 м троса для крепления мачты?

Применение теоремы Пифагора

Ответ: 43,6 м

земли нужно” .
Неизвестный катет можно найти по теореме Пифагора:
2.

S участка = Ѕ (2 + 10) х 13 = 78 (кв. вёрст);т. к. получившейся четырёхугольник- трапеция

1 верста = (русская мера длины) = 1,0668 км,

78 кв. вёрст ≈ 78 кв. км ≈ 7800 га.