Презентация на тему Понятие призмы

- прямая призма;
- наклонная

призма;
- правильная призма;
3.) Площадь полной поверхности призмы.
4.) Площадь боковой поверхности призмы.
5.) Объём призмы.
6.) Докажем теорему для треугольной призмы.
7.) Докажем теорему для произвольной призмы.
8.) Сечения призм:
- перпендикулярное сечение призмы;
9.) Призмы встречающиеся в жизни.

призмы
Параллелограммы А1А2В2В1, А1А2В2В1,… АnА1В1Вn – боковые грани
Отрезки А1В1, А2В2…АnBn

– боковые ребра призмы

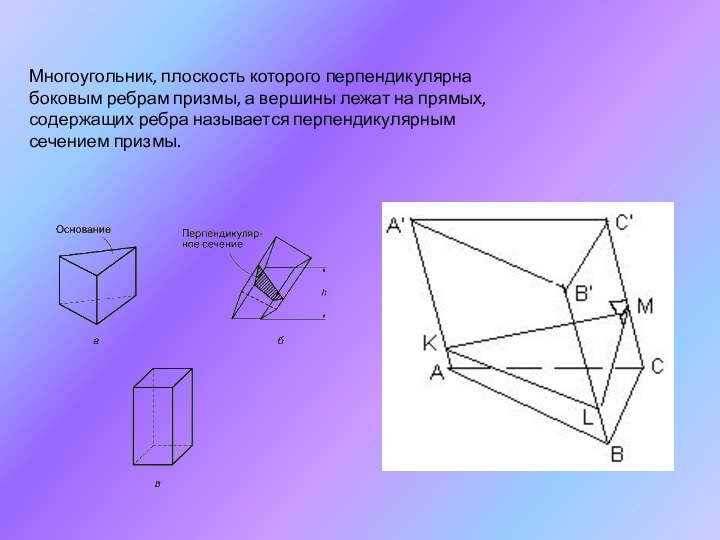
Призмой называется многогранник, у которого две грани ( основания ) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.

Грани призмы, отличные от оснований, называются боковыми гранями , а их ребра называются боковыми ребрами . Все боковые ребра равны между собой как параллельные отрезки, ограниченные двумя параллельными плоскостями. Все боковые грани призмы являются параллелограммами. Соответствующие стороны оснований призмы равны и параллельны. Поэтому в основаниях лежат равные многоугольники.
Поверхность призмы состоит из двух оснований и боковой поверхности.
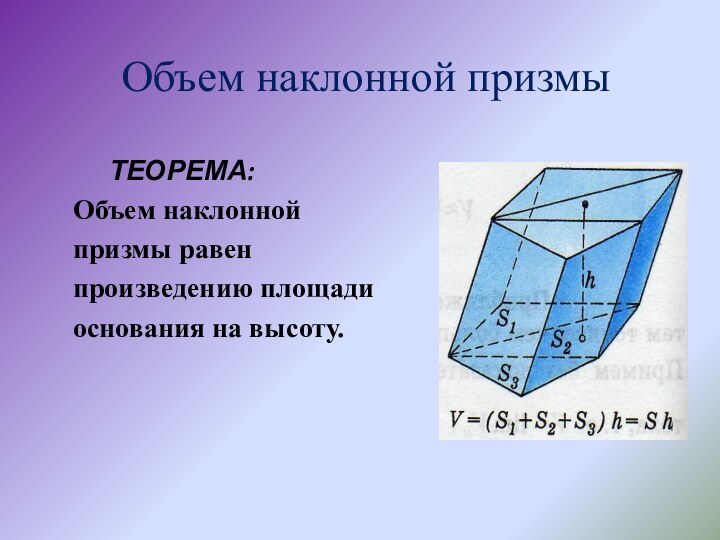
Высотой призмы называется отрезок, являющийся общим перпендикуляром плоскостей, в которых лежат основания призмы.
Высота призмы равна расстоянию h между плоскостями оснований.

Треугольная Четырехугольная

призма призма призма

ребра призмы перпендикулярны основаниям то призма называется прямой,
в

противном случае – наклонной.

ее основания - правильные многоугольники.

равна половине произведения периметра основания на высоту призмы.

призму с объемом V, площадью основания S и высотой

h. Отметим точку О на одном из оснований призмы и направим ось Ох перпендикулярно к основаниям. Рассмотрим сечение призмы плоскостью, перпендикуляр­ной к оси Ох и, значит, параллельной плоскости основания. Обозначим буквой х абсциссу точки пересе­чения этой плоскости с осью Ох, а через S (х) — площадь получившегося сечения.
Докажем, что площадь S (х) равна площади S основания призмы. Для этого заметим, что треуголь­ники ABC (основание призмы) и А1B1С1 (сечение призмы рассматриваемой плоскостью) равны. В самом деле, четырехугольник АA1BB1 — параллелограмм (отрезки АА1 и ВВ1 равны и параллельны), поэтому А1В1=АВ. Аналогично доказывается, что В1С1=ВС и А1С1=АС. Итак, треугольники А1В1С1 и ABC равны по трем сторонам. Следовательно, S(x)=S. Применяя теперь основную формулу для вычисления объемов тел при а=0 и b=h, получаем

высотой h и площадью основания S. Такую призму можно

разбить на треугольные призмы с общей высотой h. Выразим объем каждой треугольной призмы по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель h, получим в скобках сумму площадей оснований треугольных призм, т. е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен S * h.
Теорема доказана.

вершины лежат на прямых, содержащих ребра называется перпендикулярным сечением

призмы.