- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методическая разработка открытого урока по геометрии 10 класса Тема Предмет стереометрии. Аксиомы стереометрии
Содержание
- 2. ТРЁХМЕРНОЕ ПРОСТРАНСТВО – НЕ ПРОСТО МАТЕМАТИЧЕСКОЕ ПОНЯТИЕ.
- 3. Эдвин Эббот (1838-1926) учитель математики, директор одной
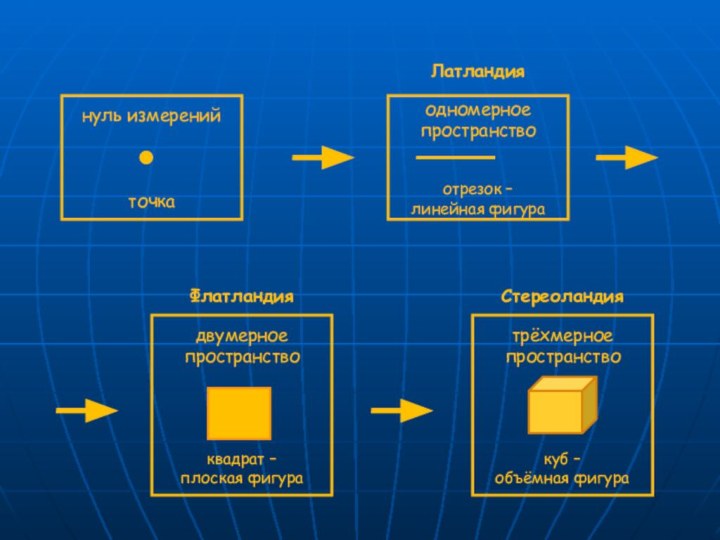
- 4. ЛатландияФлатландияСтереоландия
- 5. Первый мир – Латландия. Это мир одного
- 6. Второй мир - Флатландия. Это мир двумерного
- 7. Сочетание миров
- 8. Третий мир – Стереоландия. Трехмерное пространство –
- 9. Голландский художник Мауриц Корнелис Эшер создал очень
- 10. «Развитие» Гравюра Эшера
- 11. «Оболочка» Гравюра Эшера
- 12. «Картинная галерея» Гравюра Эшера
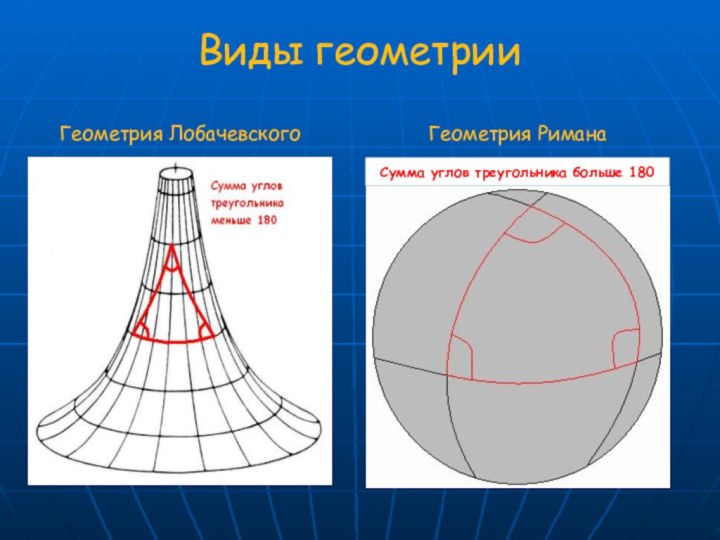
- 13. Виды геометрииIII век до н.э.Школьный курс геометрии
- 14. Виды геометрииГеометрия ЛобачевскогоГеометрия Римана
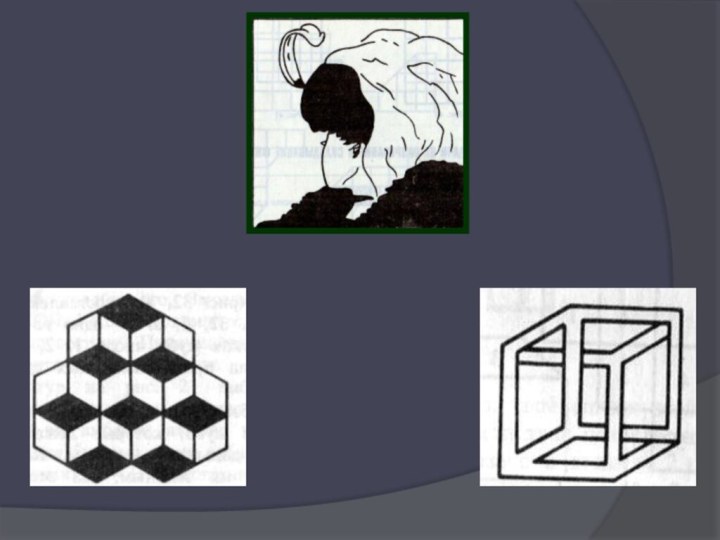
- 15. Хорошее воображение – это качество, необходимое в
- 17. С давних пор люди пытались объёмные тела
- 18. Скачать презентацию
- 19. Похожие презентации















Слайд 3 Эдвин Эббот (1838-1926) учитель математики, директор одной из
школ Лондона. более ста лет назад придумал для своих
учеников путешествие в пространства различных измерений.Попадая в разные измерения, как житель этого измерения, оживляя геометрические фигуры, он пытался показать особенности данного пространства.
Слайд 5 Первый мир – Латландия. Это мир одного измерения,
весь мир на одной прямой! Движение происходит только вперёд
и назад по данной прямой. Вселенная для латланцев – прямая, а их горизонт ограничен одной точкой, не имеющей ни одного измерения. Я увидел, как вдоль прямой двигались обитатели Латландии - …Подключите свое воображение и изобразите в тетради данный мир, себя в нём и опишите его.
Отрезки разной длины, точки. Те, кто оказался рядом , вынуждены находится рядом всегда. Я подумал, что жизнь в этом мире, должно быть невыносимо скучна: нет возможности обогнать своего соседа или отстать от него. Между тем жители Латландии выглядели вполне жизнерадостными. Мои попытки объяснить им, что можно двигаться не только , вперед и назад, но и слева направо, озадачили их, так как это означало двигаться внутрь себя. Они просили продемонстрировать им это , но услышав, что это невозможно, если они не покинут свою прямую, закричали: «Выйти за пределы прямой ? Ты хочешь сказать за пределы пространства!?»
Слайд 6 Второй мир - Флатландия. Это мир двумерного пространства,
страна двух измерений - длины и ширины, подобная книжной
страницы или классной доске. Когда я вошёл в него, то понял мы живём НА плоскости, а флатланцы – В плоскости! Её обитатели имеют вид …Подключите свое воображение и изобразите в тетради данный мир, себя в нём и опишите его.
плоских геометрических фигур. Они обладают длиной и шириной, могут свободно перемещаться во всех направлениях вдоль поверхности, но не имеют толщины и лишены возможности двигаться «верх» и «низ», т.е. перпендикулярно плоскости страницы. В этом мире нет ничего, что у нас принято называть объёмным. Чем больше углов у фигуры, тем выше сословие, а круг - их король!
Низшие сословия –точки, прямые и их дети отрезки. Поэтому простейшими фигурами плоскости являются точки, прямые! Когда я рассказывал о трехмерном пространстве, у флатланцев загорались глаза, но услышав, что надо покинуть плоскость, чтобы выйти в трехмерное пространство, они начинали с ужасом говорить: «Двигаться в верх, вниз – означает двигаться внутрь себя!»
Слайд 8 Третий мир – Стереоландия. Трехмерное пространство – это
мир , в котором мы живем. Посмотрим вокруг: трехмерны
все вещи, которые нас окружают, кроме длины и ширины они имеют ещё одно измерение - высоту или толщину. Стереоландия – это страна, где живут геометрические фигуры нашего мира.Подключите свое воображение и изобразите в тетради данный мир, себя в нём и опишите его простейшие фигуры.
Простейшими и основными фигурами трехмерного пространства являются: точки, прямые и плоскости. Наряду с этими фигурами мы будем рассматривать геометрические тела и их поверхности. Многогранники и тела вращения.
Слайд 9 Голландский художник Мауриц Корнелис Эшер создал очень много
известных гравюр о трёхмерном пространстве. В жизни этого удивительного
человека было много парадоксов. Например, рисовал он левой рукой, а писал правой.Мауриц Корнелис Эшер
Слайд 13
Виды геометрии
III век до н.э.
Школьный курс геометрии рассматривает
«евклидову геометрию», названную в честь её разработчика – древнегреческого
математика ЕвклидаСлайд 15 Хорошее воображение – это качество, необходимое в равной
мере и математику, и поэту. А может быть, математику
даже в большей степени. Великий французский просветитель Вольтер как-то сказал: «В голове у Архимеда было гораздо больше воображения, чем в голове у Гомера».В геометрии очень важно уметь смотреть и видеть, замечать различные особенности геометрических фигур, делать выводы из замеченных особенностей. Эти умения, которые вместе можно назвать «геометрическим зрением», необходимо постоянно тренировать и развивать.