Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему к уроку геометрии Сумма углов треугольника 7 класс

Содержание

2. «Быстрее всего ум, ибо он обегает все,
3. Сумма углов треугольника. Решение задач.
4. Цели урока:закрепить интересные и важные свойства треугольников;применить
5. Задачи урокапроверить знания фактического материала : теорем,
6. Известные факты, связанные с угламиопределение и свойства
12. А ты знаешь ответ? Проверь себя
13. 1. В АВС А=900, при этом другие
14. В АВС А=900, при этом другие два угла… б). оба острые;
15. 2. В АВС В – тупой, при
16. 2. В АВС В – тупой, при
17. 3. В тупоугольном треугольнике могут быть: а).
18. 3. В тупоугольном треугольнике могут быть: в). тупой и острый углы.
19. 4. В остроугольном треугольнике могут быть: а).
20. 4. В остроугольном треугольнике могут быть: а). все углы острые;
21. 5. В прямоугольном треугольнике могут быть: а).
22. 5. В прямоугольном треугольнике могут быть: в). два острых угла.
23. Методы решения 1.Решение задачи «по действиям».2.Решение задачи составлением уравнения.3.Выполнение дополнительных построений.
24. Алгоритм решения задач по действиям. 1. В
25. Домашнее задание1. Пункты 30, 31.2. Решить задачу
26. Скачать презентацию
27. Похожие презентации

«Быстрее всего ум, ибо он обегает все, Мудрее всего время, ибо оно раскрывает все. Что трудно на свете? – Познать себя.- А что легко? – Советовать другому – Кто счастлив? – Тот, кто здоров телом,

Главная
Геометрия
Презентация к уроку геометрии Сумма углов треугольника 7 класс

Ягницина Евгения АндреевнаУчитель математики, физикиГ. Северск МБОУ «СОШ № 87»Добро пожаловать на урок!

«Быстрее всего ум, ибо он обегает все, Мудрее всего время, ибо оно

Сумма углов треугольника. Решение задач.

Цели урока:закрепить интересные и важные свойства треугольников;применить важнейшую теорему геометрии – теорему

Задачи урокапроверить знания фактического материала : теорем, понятий «внешний угол треугольника», классификацию

Известные факты, связанные с угламиопределение и свойства смежных и вертикальных углов;свойство углов

Презентация к уроку геометрии Сумма углов треугольника 7 класс

1. В АВС А=900, при этом другие два угла… а). один острый,

В АВС А=900, при этом другие два угла… б). оба острые;

2. В АВС В – тупой, при этом два другие угла могут

3. В тупоугольном треугольнике могут быть: а). прямой и острый углы; б).

3. В тупоугольном треугольнике могут быть: в). тупой и острый углы.

4. В остроугольном треугольнике могут быть: а). все углы острые; б). один

4. В остроугольном треугольнике могут быть: а). все углы острые;

5. В прямоугольном треугольнике могут быть: а). прямой и тупой углы; б).

5. В прямоугольном треугольнике могут быть: в). два острых угла.

Методы решения 1.Решение задачи «по действиям».2.Решение задачи составлением уравнения.3.Выполнение дополнительных построений.

Алгоритм решения задач по действиям. 1. В ключевом треугольнике известны некоторые углы.

Домашнее задание1. Пункты 30, 31.2. Решить задачу при условии А=560.3*. Дополнительное задание:

Слайды презентации

Слайд 2 «Быстрее всего ум, ибо он обегает все, Мудрее всего

«Быстрее всего ум, ибо он обегает все, Мудрее всего время, ибо

время, ибо оно раскрывает все. Что трудно на свете? –

Познать себя.- А что легко? – Советовать другому – Кто счастлив? – Тот, кто здоров телом, Восприимчив душою и податлив на воспитание».

Слайд 3 Сумма углов треугольника. Решение задач.

Слайд 4 Цели урока:
закрепить интересные и важные свойства треугольников;
применить важнейшую

Цели урока:закрепить интересные и важные свойства треугольников;применить важнейшую теорему геометрии –

теорему геометрии – теорему о сумме углов треугольника, следствие

из теоремы, теорему о внешнем угле треугольника;
развивать логическое мышление учащихся, геометрическую интуицию;
совершенствовать навыки решения задач.

Слайд 5 Задачи урока
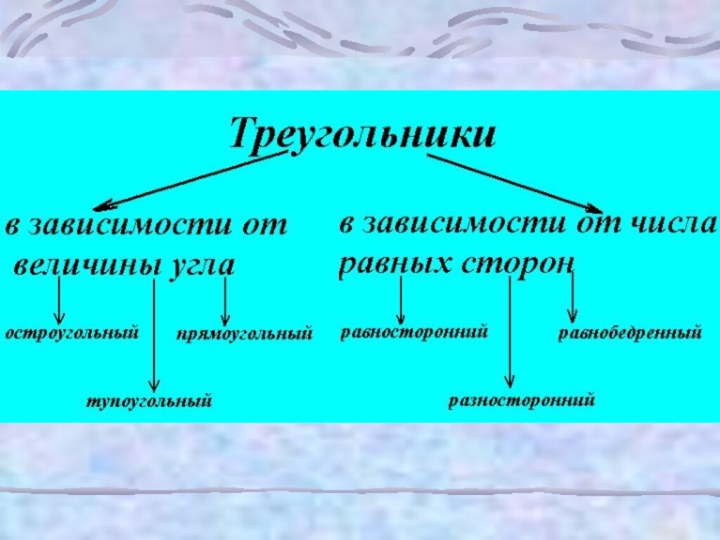
проверить знания фактического материала : теорем, понятий

Задачи урокапроверить знания фактического материала : теорем, понятий «внешний угол треугольника»,

«внешний угол треугольника», классификацию треугольников по углам;
проверить умение использовать

рациональные приемы решения задач;
проверить вычислительные навыки;
проверить уровень сформированности внимания, памяти, логических приемов мышления, применить знания в реальной, конкретной ситуации.

Слайд 6 Известные факты, связанные с углами
определение и свойства смежных

Известные факты, связанные с угламиопределение и свойства смежных и вертикальных углов;свойство

и вертикальных углов;
свойство углов при основании равнобедренного треугольника;
свойства углов,

образованных при пересечении параллельных прямых секущей;
определение биссектрисы и высоты треугольника;
теорема о сумме углов треугольника;
теорема о внешнем угле треугольника.

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12
А ты знаешь ответ?
Проверь себя

Слайд 13 1. В АВС А=900, при этом другие два

1. В АВС А=900, при этом другие два угла… а). один

угла… а). один острый, а другой может быть прямым или

тупым; б). оба острые; в). могут быть как острыми, так и прямыми или тупыми.

Слайд 14 В АВС А=900, при этом другие два угла… б).

оба острые;

Слайд 15 2. В АВС В – тупой, при этом

2. В АВС В – тупой, при этом два другие угла

два другие угла могут быть… а). только острыми; б). острыми и

тупыми; в). острыми и прямыми.

Слайд 16 2. В АВС В – тупой, при этом

два другие угла могут быть… а). только острыми;

Слайд 17 3. В тупоугольном треугольнике могут быть: а). прямой и

острый углы; б). тупой и прямой углы; в). тупой и острый

углы.

Слайд 18 3. В тупоугольном треугольнике могут быть: в). тупой и

острый углы.

Слайд 19 4. В остроугольном треугольнике могут быть: а). все углы

4. В остроугольном треугольнике могут быть: а). все углы острые; б).

острые; б). один тупой угол; в). один прямой угол.

Слайд 20 4. В остроугольном треугольнике могут быть: а). все углы

острые;

Слайд 21 5. В прямоугольном треугольнике могут быть: а). прямой и

5. В прямоугольном треугольнике могут быть: а). прямой и тупой углы;

тупой углы; б). два прямых угла; в). два острых угла.

Слайд 22 5. В прямоугольном треугольнике могут быть: в). два острых

угла.

Слайд 23 Методы решения
1.Решение задачи «по действиям».
2.Решение задачи составлением уравнения.
3.Выполнение

дополнительных построений.

Слайд 24 Алгоритм решения задач по действиям.
1. В ключевом треугольнике

Алгоритм решения задач по действиям. 1. В ключевом треугольнике известны некоторые

известны некоторые углы. Находим неизвестные углы, которые также являются

углами другого треугольника.
2. Поскольку в новом треугольнике стали известны углы, то появляется возможность определить другие углы этого треугольника и перейти к следующему и т.д.