- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
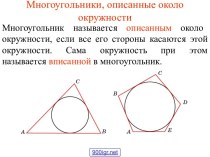
Презентация на тему к уроку-семинару площади и объемы тел
Содержание
- 2. Цели урока обобщить и систематизировать знания по теме «Логарифмы» закрепить умения решать выражения, содержащие логарифмы.
- 3. План урока: История логарифмов. Логарифмам 400 лет.Логарифмы
- 4. «Изобретение логарифмов, сократив работу астронома, продлило ему
- 5. Портретная галереяШотландский математик, изобретатель логарифмов.Учился в Эдинбургском
- 6. Логарифмическая линейка 1622 год - Первый вариант линейки разработал английский математик-любитель Уильям Отред
- 7. 1630 год -Ричард Деламейн создаёт круговую логарифмическую линейку.
- 8. Англичанин Роберт Биссакар (и независимо от него
- 9. Логарифмы в природеЛогарифмическая спираль есть математический символ
- 10. Логарифмическая спираль «Удивительное рядом»Спираль – это
- 11. Логарифмическая спираль «Удивительное рядом»
- 12. Логарифмическая спираль «Удивительное рядом»Первым ученым, открывшим
- 13. Логарифмическая спираль «Удивительное рядом»По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника
- 14. Логарифмическая спираль «Удивительное рядом»По логарифмическим спиралям выстраиваются рога многих животных
- 15. Живые существа обычно растут, сохраняя общее очертание
- 16. Логарифмическая спираль «Удивительное рядом»По логарифмической спирали свёрнуты раковины многих улиток и моллюсков.
- 18. Логарифмическая спираль «Удивительное рядом»По логарифмической спирали формируется тело циклона
- 19. Логарифмическая спираль «Удивительное рядом»Даже пауки, сплетая паутину, закручивают нити вокруг центра по логарифмической спирали.
- 20. Логарифмическая спираль «Удивительное рядом»
- 21. Логарифмическая спираль «Удивительное рядом»Траектории насекомых
- 22. Логарифмическая спираль «Удивительное рядом»
- 23. Очертания, выраженные логарифмической спиралью, имеют не только
- 24. Испуганное стадо северных оленей разбегается по спирали.
- 25. Спиралью закручиваются ураганы и смерчи
- 26. Молекула ДНК закручена двойной спиралью.
- 27. Астрономы измеряют «блеск» небесных светил в звездных величинах
- 29. Логарифмы в жизни человека
- 30. Логарифмы в музыкеДаже изящные искусства питаются еюРазве
- 31. Логарифм шума
- 32. Вращающийся нож
- 33. Логарифмическая спираль «Удивительное рядом»
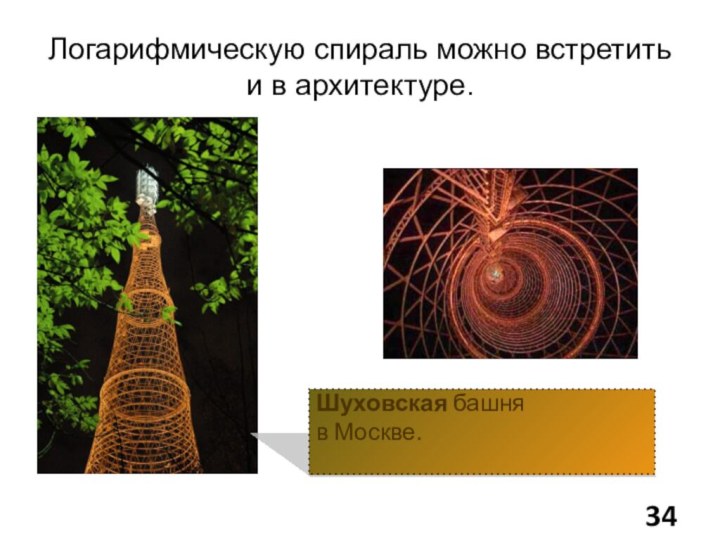
- 34. Логарифмическую спираль можно встретить и в архитектуре.Шуховская башня в Москве.
- 35. Однако в начале XXI века логарифмические линейки
- 37. Логарифмом числа b по
- 38. Самостоятельная работа
- 39. Основное логарифмическое тождествоalog ab = bЛогарифмом числа
- 40. Самостоятельная работа
- 41. Свойства логарифмовПусть а>0, а≠1, b>0, с>0, тогда
- 42. Решите тест1. Вычислить: lg 5 + lg
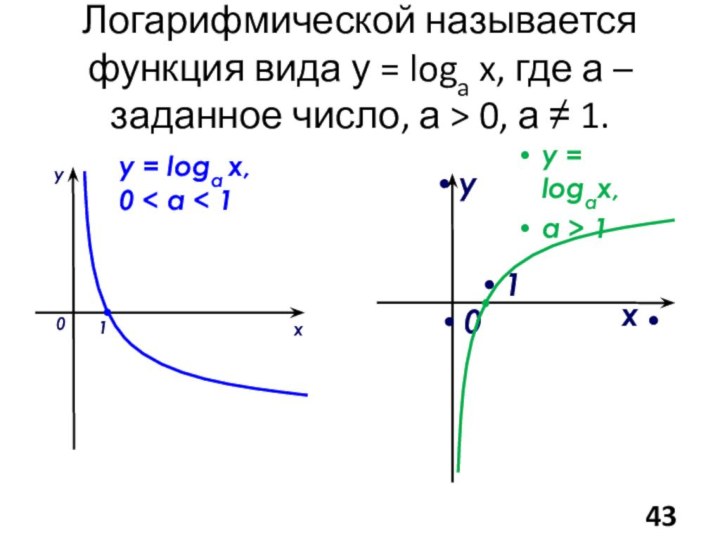
- 43. Логарифмической называется функция вида у = loga
- 44. а) При а > 1 функция возрастает
- 45. Самостоятельная работа Расположите в порядке возрастания
- 46. Самостоятельная работа: а) log2(2 – х) =
- 47. Скачать презентацию
- 48. Похожие презентации
Цели урока обобщить и систематизировать знания по теме «Логарифмы» закрепить умения решать выражения, содержащие логарифмы.











































Слайд 3
План урока:
История логарифмов. Логарифмам 400 лет.
Логарифмы в
природе.
Применение логарифмов в различных сферах жизнедеятельности человека
Определение логарифма. Основное
логарифмическое тождество. Свойства логарифмов.Логарифмическая функция и ее свойства.
Решение логарифмических уравнений и неравенств.
Слайд 4 «Изобретение логарифмов, сократив работу астронома, продлило ему жизнь»
П.С.Лаплас
История логарифмов
Слайд 5
Портретная галерея
Шотландский математик, изобретатель логарифмов.
Учился в Эдинбургском университете.
Основными идеями учения о логарифмах Непер овладел не позднее
1594 г., однако его "Описание удивительной таблицы логарифмов", в котором изложено это учение, было издано в 1614 г.В этом труде содержались определение логарифма, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
В "Построении удивительной таблицы логарифмов" (опубликовано в 1619) Непер изложил принцип вычисления таблиц.
Непер Джон
(1550 - 1617)
Слайд 6
Логарифмическая линейка
1622 год - Первый вариант
линейки разработал английский математик-любитель Уильям Отред
Слайд 8 Англичанин Роберт Биссакар (и независимо от него в
1657 году — С.Патридж) разработал прямоугольную логарифмическую линейку, конструкция
которой в основном сохранилась до наших дней.
Слайд 9
Логарифмы в природе
Логарифмическая спираль есть математический символ жизни
и духовного развития.
Иоганн-Вольфганг Гёте
Слайд 10
Логарифмическая спираль
«Удивительное рядом»
Спираль – это плоская кривая
линия, многократно обходящая одну из точек на плоскости, которая
называется полюсом спирали.
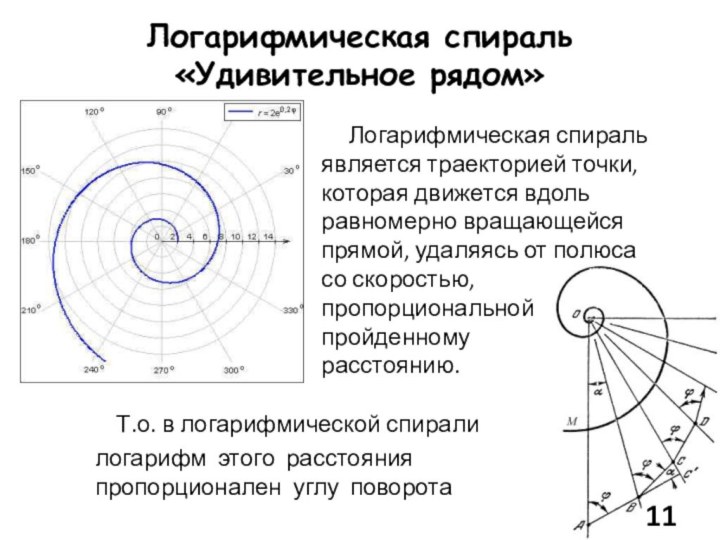
Слайд 11
Логарифмическая спираль
«Удивительное рядом»
Логарифмическая спираль
является
траекторией точки, которая движется вдоль равномерно вращающейся прямой, удаляясь от полюса
со скоростью,
пропорциональной
пройденному
расстоянию.
Т.о. в логарифмической спирали
логарифм этого расстояния пропорционален углу поворота
Слайд 12
Логарифмическая спираль
«Удивительное рядом»
Первым ученым, открывшим эту удивительную
кривую, был
французский математик
Рене Декарт (1596-1650гг.)
Самое интересное и удивительное в том, что логарифмическая спираль возникает в нашей жизни в связи с самыми разными природными формами.
Слайд 13
Логарифмическая спираль
«Удивительное рядом»
По логарифмическим спиралям выстраиваются
цветки
в соцветиях подсолнечника
Слайд 14
Логарифмическая спираль
«Удивительное рядом»
По логарифмическим спиралям выстраиваются
рога
многих животных
Слайд 15 Живые существа обычно растут, сохраняя общее очертание своей
формы. При этом они растут чаще всего во всех
направлениях - взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении.Логарифмическая спираль
«Удивительное рядом»
Слайд 16
Логарифмическая спираль
«Удивительное рядом»
По логарифмической спирали свёрнуты
раковины
многих улиток и моллюсков.
Слайд 18
Логарифмическая спираль
«Удивительное рядом»
По логарифмической спирали формируется
тело циклона
Слайд 19
Логарифмическая спираль
«Удивительное рядом»
Даже пауки, сплетая паутину,
закручивают нити вокруг центра по логарифмической спирали.
Слайд 20
Логарифмическая спираль
«Удивительное рядом»
улитка
Человеческое ухо
– это маленькое чудо!
Улитка является органом, воспринимающим звук, в
котором самой природой заложенаЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ!
Слайд 21
Логарифмическая спираль
«Удивительное рядом»
Траектории насекомых
летящих на
свет также описывают логарифмическую спираль.
**************************
Логарифмическая спираль единственная из
спиралей не меняет своей формы при увеличении размеров. Видимо, это свойство и послужило причиной того, что в живой природе логарифмическая спираль встречается чаще других.
Слайд 22
Логарифмическая спираль
«Удивительное рядом»
По логарифмическим
спиралям закручены многие галактики, в частности Галактика, которой принадлежит
Солнечная система.Слайд 23 Очертания, выраженные логарифмической спиралью, имеют не только раковины.
Спираль увидели в шишках сосны, ананасах, кактусах и т.д.
Слайд 30
Логарифмы в музыке
Даже изящные искусства питаются ею
Разве музыкальная
гамма не есть -
Набор передовых логарифмов?
Из «Оды экспоненте»
А.А.
Эйхенвальд
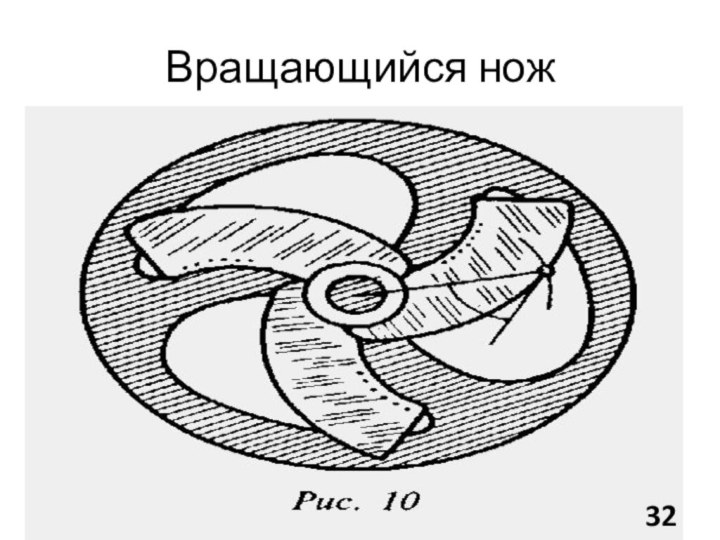
Слайд 31
Логарифм шума
Единица
измерения децибел используется в звуковой технике.
Связано это с тем, что мы реагируем не на абсолютные, а на относительные изменения уровня какого-либо воздействия, в том числе и звукового. Если сила звука (интенсивность, I, Вт/м2) изменится в 10 раз, то субъективное ощущение громкости — всего лишь на одну ступеньку, при 100-кратном увеличении силы звука — на две (lg100 = 2), при 1000-кратном — на три (lg1000 = 3). Поэтому увеличение или уменьшение силы звука принято измерять в логарифмических единицах и каждое десятикратное изменение силы звука оценивается единицей, называемой Бел (Б). На практике используется в основном единица, равная десятой части Бела - децибел.
Значение в децибелах равно десяти десятичным логарифмам отношения интенсивностей двух сигналов.
Слайд 35 Однако в начале XXI века логарифмические линейки получили
второе рождение в наручных часах. Дело в том, что,
следуя моде, производители дорогих и престижных марок часов перешли от электронных хронометров с ЖК-экранами к стрелочным и места для встраиваемого калькулятора оказалось недостаточно. Однако спрос на хронометры со встроенным вычислительным устройством среди следящих за модой людей заставил производителей часов выпустить модели с встроенной логарифмической линейкой, выполненной в виде вращающихся колец со шкалами вокруг циферблата. По прихоти производителей такие устройства обычно называются «навигационная линейка». Их достоинство — можно сразу, в отличие от микрокалькулятора, получить таблицу (например, расхода топлива на пройденное расстояние, перевода миль в километры и т. п.).
Слайд 37
Логарифмом числа b по основанию а
называется показатель степени, в которую нужно возвести
основание а, чтобы получить число b.logab = k, ak = b,
a > 0, a ≠ 1, b > 0
Слайд 39
Основное логарифмическое тождество
alog ab = b
Логарифмом числа b
по основанию а называется показатель степени, в которую нужно
возвести основание а, чтобы получить число b.
Слайд 42
Решите тест
1. Вычислить: lg 5 + lg 2.
1) lg7; 2) 1;
3) 0; 4)10.2. Вычислить: log2 15 – log2 15/16.
1) 4; 2) -4; 3)1/4; 4) -1/4.
3. Вычислить: log13 5√169.
1)2,5; 2)-2,5; 3)2/5; 4)-2/5.
4. Найти значение выражения: log8 12 – log8 15 + log8 20.
1) 2; 2) 4/3; 3) 3/4 4) 1/2.
5. Вычислить: log3 8
log3 2
1) 3; 2) 1/3 3) -3; 4)-1/3.
Слайд 44 а) При а > 1 функция возрастает на
(0; +∞);
б) при 0 < а < 1 функция
убывает на (0; +∞).Свойства логарифмической функции y = logах, а ≠ 1, a > 0
Ни четная функция, ни нечетная.
График проходит через точку (1; 0)
D(y) = (0; +∞),
2. E(y) = (-∞; +∞).
Слайд 45
Самостоятельная работа
Расположите в порядке возрастания числа
log0,3 3;
log0,30,3; log0,31;Какое из данных чисел положительное?
1) log1,1 0,1;
2) log11 0,5;
3) lg 0,9;
4) log0,10,5.
Найдите область определения функции
y= log5(x + 3)