- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Объем пирамиды 11 класс
Содержание
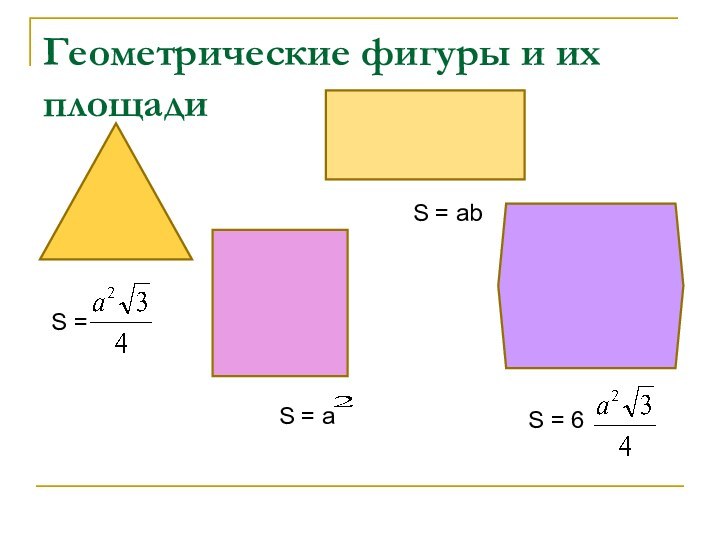
- 2. Геометрические фигуры и их площадиS = S = aS = abS = 6
- 3. 1.Определение- многоугольник АВСДЕ… лежит в плоскоститочка М не лежит в плоскостиМАВСДЕ…-пирамида
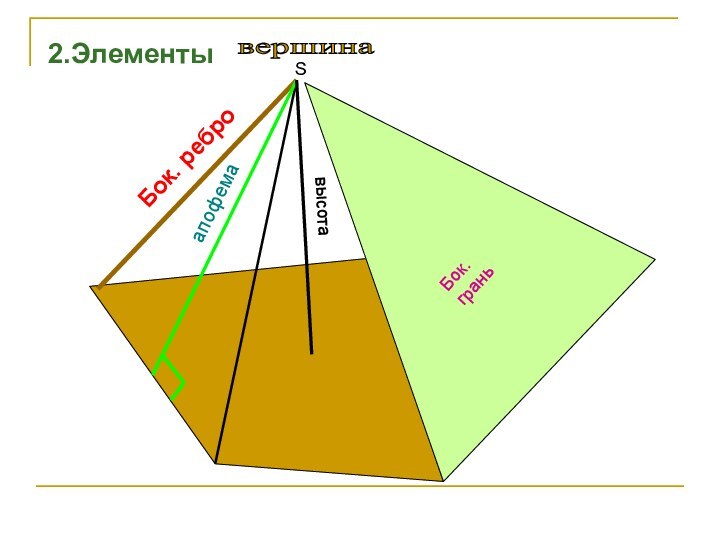
- 4. Sвершина высотаапофемаБок.грань2.ЭлементыБок. ребро
- 5. Название пирамиды определяетсяпо названию многоугольника,лежащего в основании
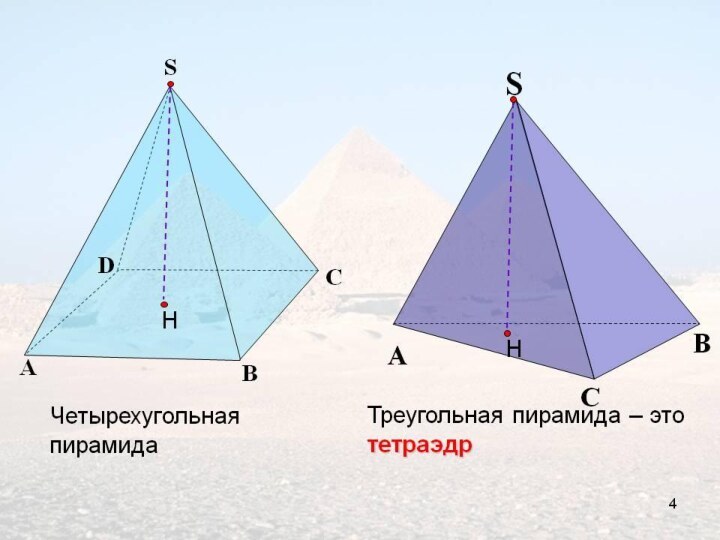
- 6. n=4Четырехугольная пирамидаПирамида Хеопсав Гизе (долина царей).
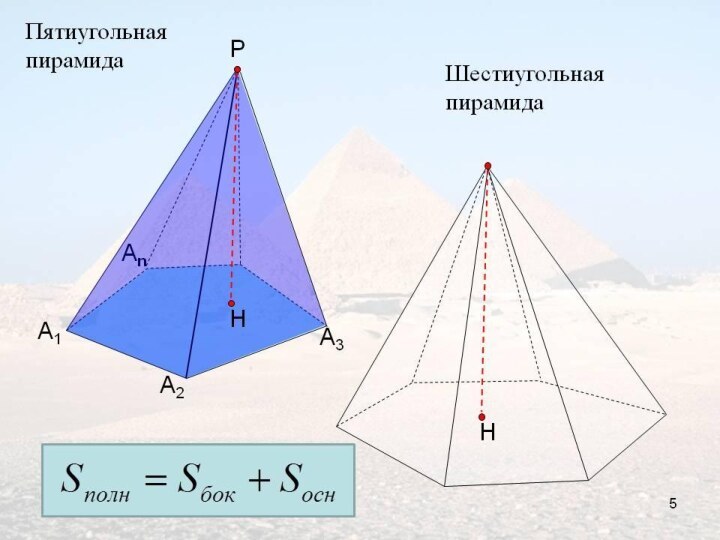
- 7. n=6Шестиугольная пирамида
- 8. Правильная пирамида1.Основание - правильный многоугольник2.Вершина проецируется в центр многоугольника
- 9. ПирамидаПирамидой ( SABCD ) называется многогранник, который
- 10. КО – высота пирамидыВОК2ВЗадача
- 11. Пирамиды вокруг нас«А в немой дали застыли
- 12. Пирамиды с разных сторонМатематикаИсторияИсследование мировой системы пирамидИсследование свойств пирамидАрхитекторы
- 13. Математическая точка зренияЕвклид пирамиду определяет как телесную
- 14. Скачать презентацию
- 15. Похожие презентации
Геометрические фигуры и их площадиS = S = aS = abS = 6





Слайд 3
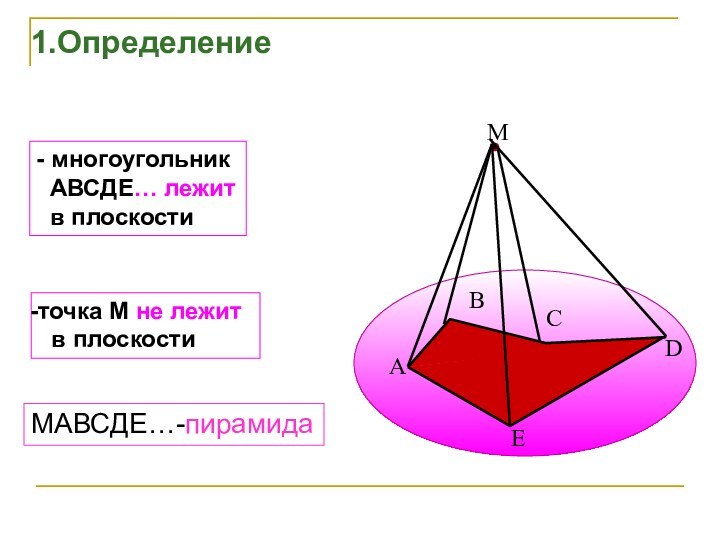
1.Определение
- многоугольник
АВСДЕ… лежит
в плоскости
точка М не
лежит
в плоскости
МАВСДЕ…-пирамида
Слайд 5
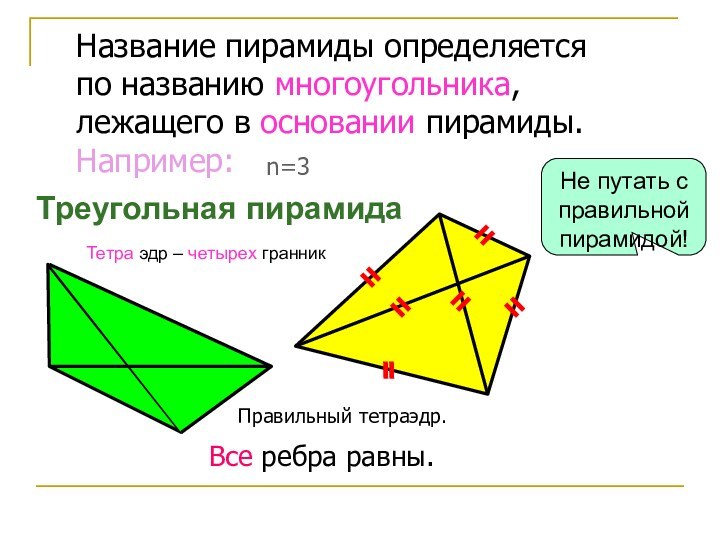
Название пирамиды определяется
по названию многоугольника,
лежащего в основании пирамиды.
Например:
n=3
Треугольная
пирамида
Не путать с правильной пирамидой!
Правильный тетраэдр.
Все ребра равны.
Тетра
эдр – четырех гранник
Слайд 8
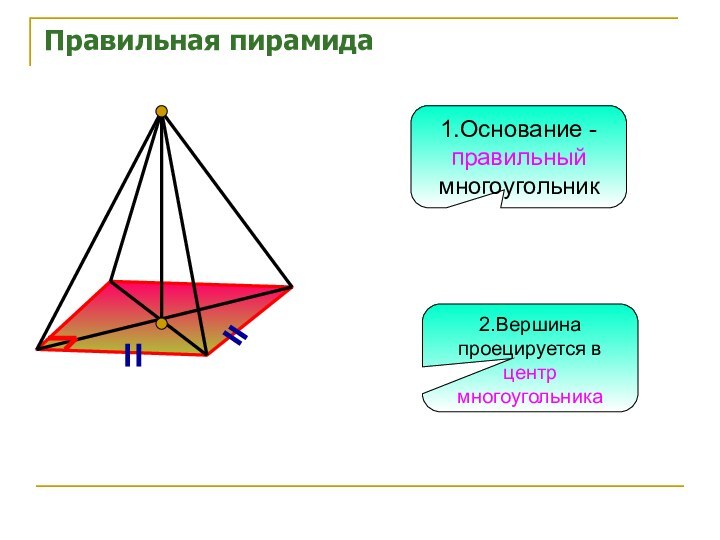
Правильная пирамида
1.Основание -
правильный многоугольник
2.Вершина проецируется в центр
многоугольника
Слайд 9
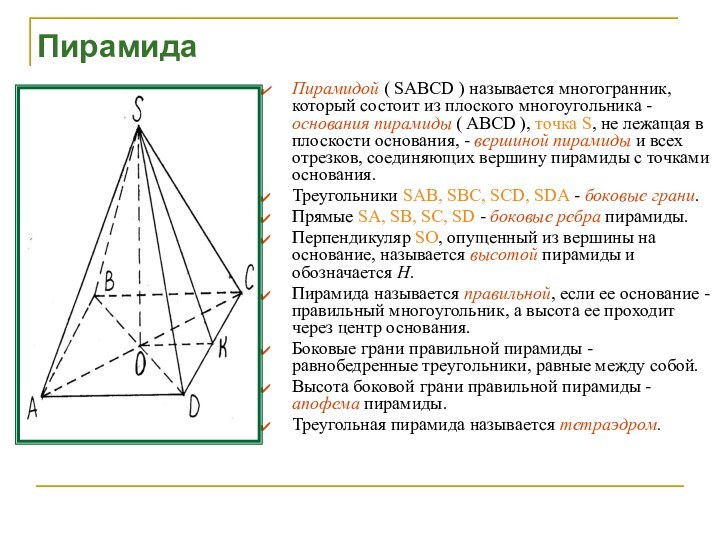
Пирамида
Пирамидой ( SABCD ) называется многогранник, который состоит
из плоского многоугольника - основания пирамиды ( ABCD ),
точка S, не лежащая в плоскости основания, - вершиной пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.Треугольники SAB, SBC, SCD, SDA - боковые грани.
Прямые SA, SB, SC, SD - боковые ребра пирамиды.
Перпендикуляр SO, опущенный из вершины на основание, называется высотой пирамиды и обозначается Н.
Пирамида называется правильной, если ее основание - правильный многоугольник, а высота ее проходит через центр основания.
Боковые грани правильной пирамиды - равнобедренные треугольники, равные между собой.
Высота боковой грани правильной пирамиды - апофема пирамиды.
Треугольная пирамида называется тетраэдром.
Слайд 10
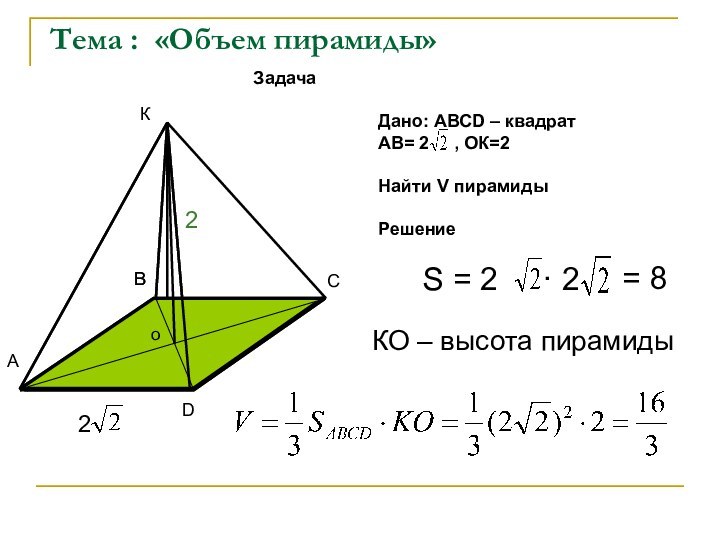
КО – высота пирамиды
В
О
К
2
В
Задача
Дано: АВСD – квадрат
АВ= 2 , ОК=2
Найти V пирамиды
Решение
S = 2 · 2
= 8
Тема : «Объем пирамиды»
А
С
D
Слайд 11
Пирамиды вокруг нас
«А в немой дали застыли пирамиды
фараонов,
саркофаги древней были.
Величавые как вечность, молчаливые как смерть.»
Михай Эминеску
Слайд 12
Пирамиды с разных сторон
Математика
История
Исследование мировой системы пирамид
Исследование свойств
пирамид
Архитекторы
Слайд 13
Математическая точка зрения
Евклид пирамиду определяет как телесную фигуру,
ограниченную плоскостями, которые от одной плоскости сходятся к одной
точке.Герон предложил следующее определение пирамиды: «Это фигура, ограниченная треугольниками, сходящимися в одной точке и основанием которой служит многоугольник».