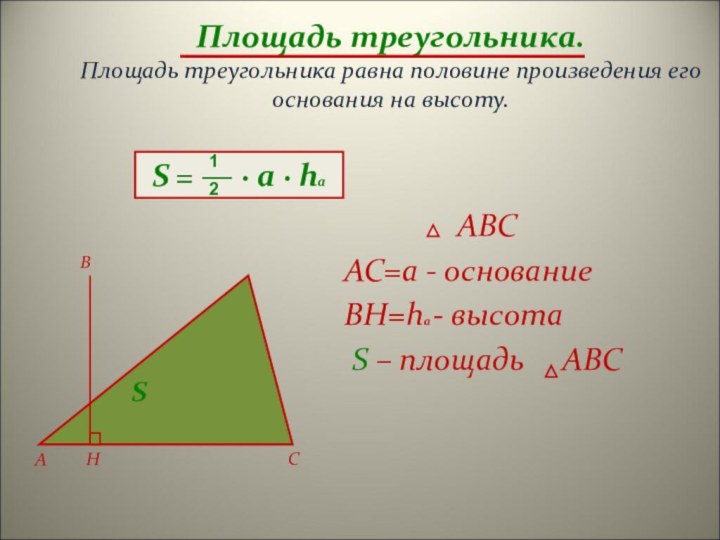
на высоту.
ABCAC=a - основание
BH=ha - высота
S – площадь ABC
A
B
C
H
S = — · a ∙ ha
1
2
S
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



A
B
C
H
S = — · a ∙ ha
1
2
S
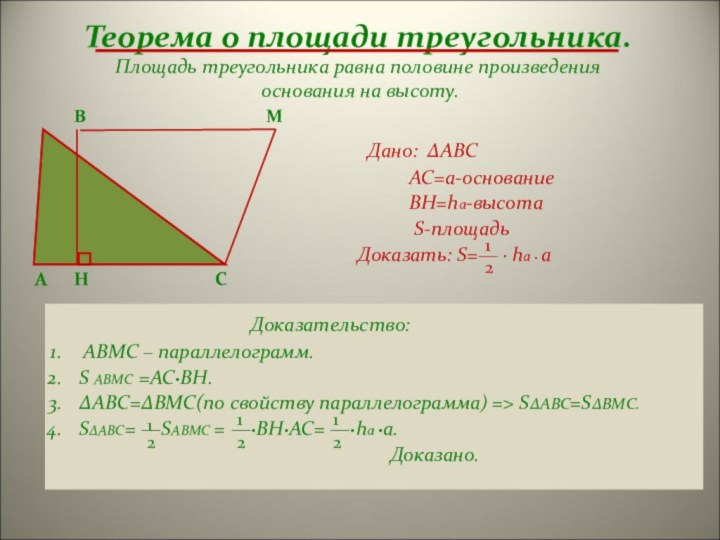
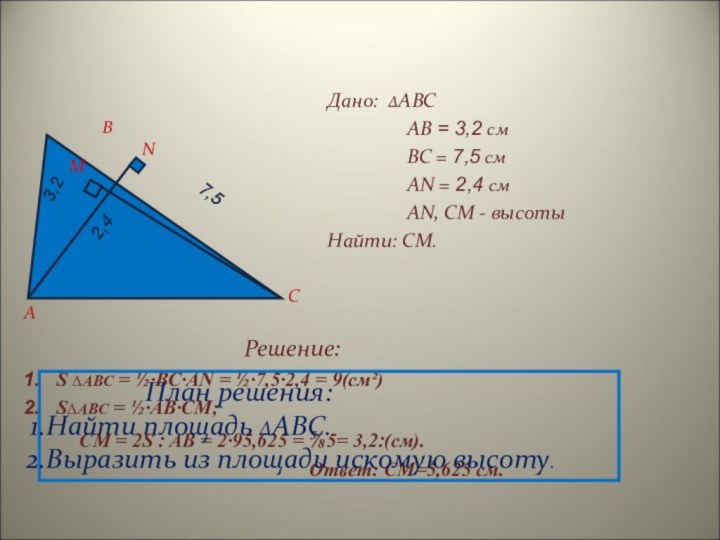
Дано: ∆ABC
AC=a-основание
BH=ha-высота
S-площадь
Доказать: S=— · ha · a
A
B
C
H
M
2
1
1
2
1
2
1
2
A
B
C
H
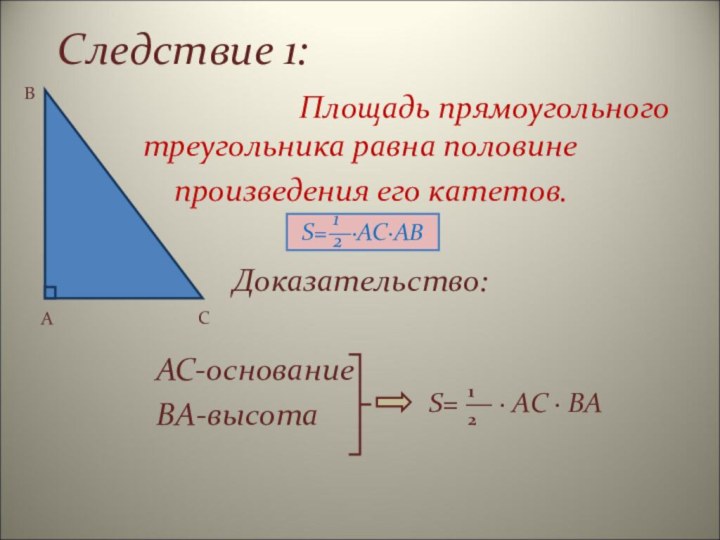
S=—∙AC∙AB
1
2
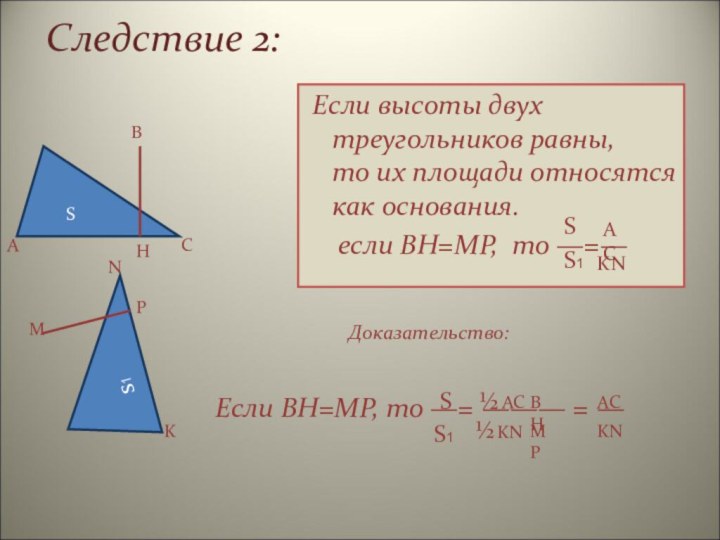
Если высоты двух треугольников равны, то их площади относятся как основания.
если BH=MP, то —=—
S
S1
A
B
C
M
N
K
H
P
S
S1
½
½
AC
BH
KN
MP
AC
KN
S
S1
AC
KN
Следствие 2:
S=— ∙a ∙ ha
1
2
a
ha
2s
ha
2)ha=—.
2s
a
S
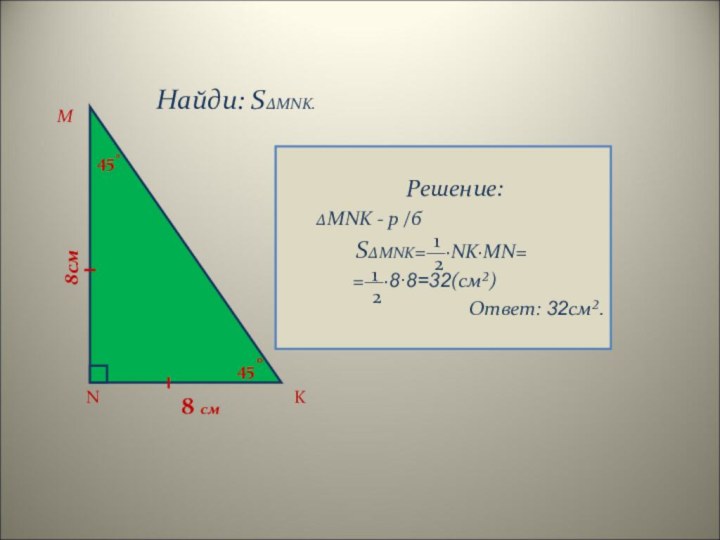
Применение теоремы о площади треугольника к решению задач.
N
M
K
45˚
8 см
45˚
8см
1
2
1
2
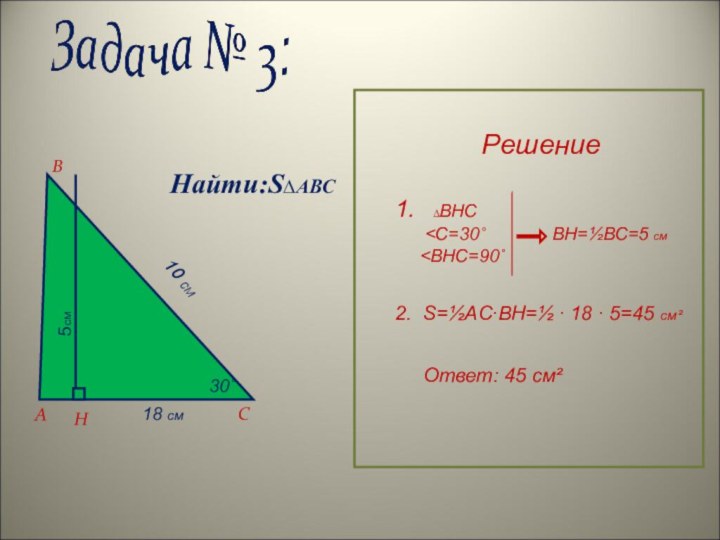
Решение:
S ∆ABC = ½∙BC∙AN = ½∙7,5∙2,4 = 9(см²)
S∆ABC = ½∙AB∙CM;
CM = 2S ׃ AB = 2∙9׃3,2 =5⅝ = 5,625(см).
Ответ: CM=5,625 см.
A
B
C
M
N
7,5
3,2
2,4
План решения:
Найти площадь ∆ABC.
Выразить из площади искомую высоту.