- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку геометрия в 8 классе по теме Обобщающий урок по теме окружности
Содержание
- 2. Итак, что же такое окружность?Окружностью называется геометрическая
- 3. История окружности Основные определения Некоторые теоремы Метрические соотношения в окружности Содержание
- 4. Окружность - одна из древнейших геометрических
- 5. Уже в латинской рукописи XI в.
- 6. Отрезок, соединяющий две точки
- 7. Любые
- 8. Вписанный угол – угол, вершина
- 9. Теорема 1Вписанный угол измеряется половиной дуги, на
- 10. Луч ВО делит угол АВС на два
- 11. Теорема 2Угол, образованный касательной и хордой, проведенной
- 12. Теорема 3Если R – радиус окружности, описанной
- 13. Итак,
- 14. ЗадачаДве окружности радиусов 5 и 7 проходят
- 15. то есть
- 16. Рассмотрим равнобедренный треугольник AO1B. Центральный угол AO1B,
- 17. Теорема 4Центр описанной около треугольника окружности –
- 18. ЗадачаРадиус окружности, проходящей через три вершины ромба,
- 19. Тогда в обоих случаях, так как АВСD
- 20. Метрические соотношения в окружностиТеорема 5 (о
- 21. Задача 1Из точки А проведены к окружности
- 22. Из теоремы косинусов для треугольника АМК:АК² =
- 23. Задача 2Через вершины А и В прямоугольного
- 24. Таким образом, АВ² – СВ² = СВ
- 25. Скачать презентацию
- 26. Похожие презентации























Слайд 3
История окружности
Основные определения
Некоторые теоремы
Метрические
соотношения в окружности
Содержание
Слайд 4 Окружность - одна из древнейших геометрических фигур.
Согласно Аристотелю, небесная материя, из которой состоят планеты
и звезды, как самая совершенная, должна двигаться по самой совершенной линии – окружности. Ещё вавилоняне и древние индийцы считали самым важным элементом окружности радиус. Слово это – латинское и означает «луч».
Термин «радиус» впервые встречается в «Геометрии» Рамуса, затем у Ф. Виета. Термин «радиус» становится общепринятым в конце XVII в.
Слайд 5 Уже в латинской рукописи XI в. «Искусство
геометрии» Боэция встречается термин «полудиаметр». Его употребляли также Фибоначчи
и Неморарий (XIII в.), Региомонтан (XV в.) и Тарталья (XVI в.).Термин «хорда» (от греческого «хорде» - струна) был введен в современном смысле европейскими учеными XII – XIII вв.
Тот факт, что диаметр делит круг и окружность на две равные части, был известен ещё в древности задолго до Фалеса Милетского.
Теоремы о зависимости между хордами и расстоянием их от центра изложены в III книге «Начал» Евклида.
Слайд 6 Отрезок, соединяющий две точки окружности,
называется ее хордой (АВ). Хорда, проходящая через центр окружности,
называется диаметром (d).Прямая, проведенная из точки, расположенной вне окружности, и имеющая только одну, общую с окружностью точку, называется касательной к этой окружности.
Прямая, имеющая с окружностью две общие точки, называется секущей.
Слайд 7
Любые две
точки окружности делят ее на две части. Каждая из
этих частей называется дугой окружности (АВ).Часть плоскости, ограниченная окружностью, называется кругом.
Центральный угол – угол, вершина которого лежит в центре окружности. Величина центрального угла равна величине соответствующей дуги (выраженной в радианах или градусах).
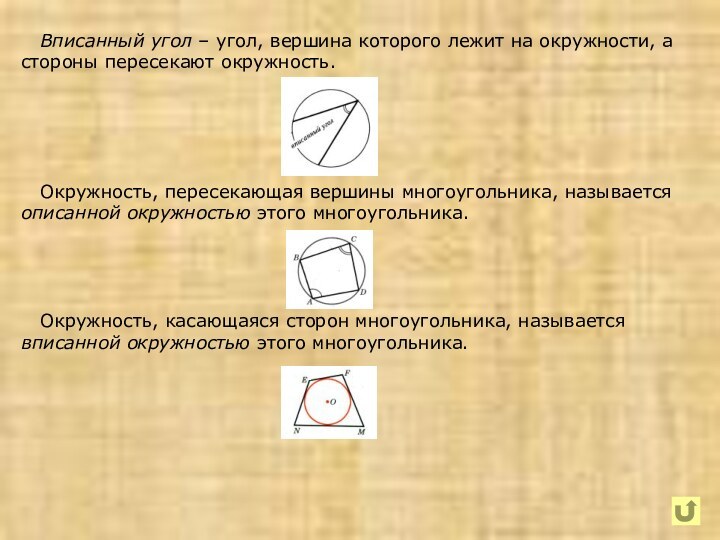
Слайд 8 Вписанный угол – угол, вершина которого
лежит на окружности, а стороны пересекают окружность.
Окружность, пересекающая вершины многоугольника, называется описанной окружностью этого многоугольника.
Окружность, касающаяся сторон многоугольника, называется вписанной окружностью этого многоугольника.
Слайд 9
Теорема 1
Вписанный угол измеряется половиной дуги, на которую
он опирается.
Доказательство
Рассмотрим три возможных случая расположения луча ВО относительно
угла АВС.1. Луч ВО совпадает с одной из сторон угла АВС, например, со стороной ВС.
АОС – внешний для равнобедренного треугольника АВО, 1 и 2 при основании равнобедренного треугольника равны, значит
АОС = 1+ 2 = 2 1.
Следовательно,
2 1 = дуге АС или АВС = 1 = половине дуги АС.
1)
2)
3)
Слайд 10
Луч ВО делит угол АВС на два угла.
Луч ВО пересекает дугу АС в некоторой точке
D. Точка D разделяет дугу АС на две дуги: АD и DС. По доказанному в п.1АВD = половине дуги АD и DВС = половине дуги DС. Складывая попарно, получаем:
АВD + DВС = половине дуги АD +половина дуги DС,
или АВС = половине дуги АС.
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
По доказанному в п.1 АВD = половине дуги АD. По аналогии СВD = половине дуги СD. Вычтем одно равенство из другого
АВD – СВD = половине дуги АD – половина дуги СD,
или АВС = половине дуги АС.
Слайд 11
Теорема 2
Угол, образованный касательной и хордой, проведенной через
точку касания, измеряется половиной дуги, заключенной между сторонами этого
угла.Доказательство
ВD перпендикулярен к касательной, угол АВD дополняет до 90˚ угол между хордой АВ и касательной. ВАD прямой. Значит, АDВ также дополняет до 90˚ АВD. Таким образом, рассматриваемый угол равен
АDВ и измеряется половиной указанной дуги.
Слайд 12
Теорема 3
Если R – радиус окружности, описанной около
треугольника АВС, то выполняются равенства
= = = 2R
Доказательство
Пусть в треугольнике АВС АВ = с, ВС = а, СА = в. Докажем, что
= =
По теореме о площади треугольника S = ав sin C, S = вс sin А,
S = са sin В.
Из первых двух равенств получаем ав sin C = вс sin А,
откуда = .
Из второго и из третьего равенств следует = .
Слайд 13 Итак,
=
=Теперь докажем, что = 2R, или ВС = 2R sin А
Проведем диаметр ВА1 и рассмотрим треугольник А1ВС.
Угол С этого треугольника прямой, поэтому ВС = ВА1 sin А1, но sin А1 = sin А. Действительно, если точка А1 лежит на дуге ВС, то А1 = А, значит sin А1 = sin А. Следовательно, ВС = ВА1 sin А, или ВС = 2R sin А.
2) Точки А1 и С совпадают, = . Угол В прямой, так
как опирается на угол в 90º, значит = АС (sin 90 = 1),
а АС = диаметру = 2R.
Следовательно, ВС = 2R sin А.
Теперь попробуем решить задачу, используя данную теорему.
Слайд 14
Задача
Две окружности радиусов 5 и 7 проходят через
вершину А треугольника АВС и касаются стороны ВС в
точках В и С соответственно. Найдите радиус окружности, описанной около треугольника АВС.Решение
Рассмотрим две окружности с радиусами R1 = 5 и R2 = 7 с общей касательной ВС. По условию окружности имеют общую точку А. Тогда либо они касаются, и тогда треугольник АВС определен однозначно, либо пересекаются в двух точках A′ и A′′.
Покажем, что во втором случае радиусы окружностей, описанных около треугольников A′BC и A′′BC равны.
Пусть R′ и R′′ - соответственно их радиусы, угол A′BC = , угол A′CB = . Рассмотрим треугольник A′BC. Получаем,
BA′C = 180º - - ,
= = = 2R′,
Слайд 15 то есть
= 2R′.
Рассмотрим треугольник A′′BC. Так как
A′BC - угол между хордой A′В и касательной ВС, A′A′′B опирается на хорду A′В, тоA′A′′B= A′BC = .
Аналогично, A′A′′C = A′CB = .
Таким образом, BA′′C = + . Из треугольника A′′BC получаем,
= 2R′′.
Следовательно R′ = R′′ = .
Таким образом, для решения задачи достаточно рассмотреть один случай, когда точка А совпадает, например, с точкой A′. Радиус R описанной около треугольника АВС окружности удовлетворяет равенствам
R = , R = , то есть R² = · .
Слайд 16
Рассмотрим равнобедренный треугольник AO1B. Центральный угол AO1B, опирающийся
на хорду АВ, в два раза больше угла между
этой хордой и касательной, то есть AO1B = 2 . Проведем высоту O1P, перпендикулярную АВ, которая является также и биссектрисой угла AO1B. Тогда в прямоугольном треугольнике O1BPBO1P = , ВР = АР = ,
sin = = , то есть = R1, аналогично = R2.
Таким образом, R² = R1 · R2, R = =
Ответ: .
Слайд 17
Теорема 4
Центр описанной около треугольника окружности – точка
пересечения серединных перпендикуляров к сторонам.
Доказательство
Серединный перпендикуляр к отрезку представляет
собой геометрическое место точек, равноудаленных от его концов. Поэтому, если мы проведем два серединных перпендикуляра к сторонам АВ и ВС треугольника АВС, то точка их пересечения (а они обязательно пересекутся, так как перпендикуляры к не параллельным прямым пересекаются) будет равноудалена от вершин А и В, а также от В и С. Таким образом, получившаяся точка О равноудалена от всех трех вершин треугольника, и окружность с центром в О и радиусом ОА проходит через все вершины треугольника и является описанной окружностью. Понятно, что через О проходит и серединный перпендикуляр к АС. Теперь попробуем решить задачу, используя данную теорему.
Слайд 18
Задача
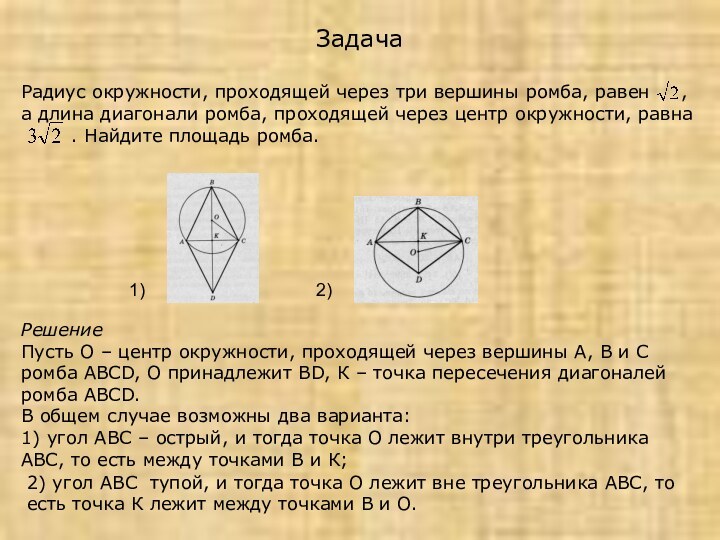
Радиус окружности, проходящей через три вершины ромба, равен
, а длина диагонали ромба, проходящей через
центр окружности, равна. Найдите площадь ромба.
Решение
Пусть О – центр окружности, проходящей через вершины А, В и С ромба АВСD, О принадлежит ВD, К – точка пересечения диагоналей ромба АВСD.
В общем случае возможны два варианта:
1) угол АВС – острый, и тогда точка О лежит внутри треугольника АВС, то есть между точками В и К;
2) угол АВС тупой, и тогда точка О лежит вне треугольника АВС, то есть точка К лежит между точками В и О.
1)
2)
Слайд 19 Тогда в обоих случаях, так как АВСD –
ромб, то его диагонали перпендикулярны и делятся точкой пересечения
пополам:ВК = КD = = ,
АК = КС = .
ОВ = ОС = (радиусы окружности). Так как по условию ВК > ОВ, то возможен только первый случай. Таким образом,
ОК = КВ – ОВ = .
Из теоремы Пифагора для прямоугольного треугольника ОКС получаем
КС² = ОС² - ОК², КС = , АС = .
= = .
Ответ: .
Слайд 20
Метрические соотношения в окружности
Теорема 5 (о секущих)
Если
через точку М вне окружности провести две секущие, то
произведения длин секущих на их внешние части будут равны: МА · МВ = МС · МD.Данную теорему примем без доказательства.
Теорема 6 (о секущей и касательной)
Если через точку М вне окружности провести секущую и касательную, то произведение длины секущей на её внешнюю часть будет равно квадрату длины касательной: МА · МВ = МК².
Данную теорему примем без доказательства.
Решим несколько задач, используя данные теоремы.
Слайд 21
Задача 1
Из точки А проведены к окружности радиуса
2 касательная АМ (М – точка касания) и секущая,
пересекающая окружность в точках К и L. Известно, что L – середина отрезка АК, угол АМК = 60º. Найдите площадь треугольника АМК.Решение
Заметим, что угол КМО = углу АМО – угол АМК, угол КМО = 90 – 60 = 30º. Рассмотрим треугольник МОК:
МО = ОК = 2,
Угол ОКМ = углу КМО = 30º, угол МОК = 120º.
По теореме синусов = , откуда получим
МК = = 2 .
Пусть x – длины отрезков АL и LK. По теореме о касательной и секущей АL · LK = АМ².
Или x · 2x = АМ².
Следовательно, АМ = x .
Слайд 22
Из теоремы косинусов для треугольника АМК:
АК² = АМ²
+МК² – 2АМ · МК cos 60º,
(2x)² =
(x )² + (2 )² - 2x · 2 · ,или
x² + x – 6 = 0.
Тогда
х1 = , х2 = .
По смыслу задачи x > 0, x = · AM = · .
Вычислим теперь площадь треугольника АМК:
S = AM · MK sin 60º = · 2 = 1,5( ).
Ответ: 1,5( ).
Слайд 23
Задача 2
Через вершины А и В прямоугольного треугольника
АВС (угол С – прямой) проведена окружность, касающаяся стороны
АС и пересекающая продолжение стороны ВС в точке D. Найдите радиус окружности, если известно, что АВ = 3 см и СD = 3,2см. Решение
Обозначим искомый радиус через R. Из точки О опустим перпендикуляр ОК на продолжение стороны СВ. По свойству касательной АС перпендикулярен к ОА, АОКС – прямоугольник и
СК = АО = R, KD = CD - R.
Так как ОК перпендикулярен к ВD, то ВК = КD,
CB = CK – BK = R – (CD – R) = 2R – CD.
Следовательно, R = + 1,6.
Найдем СВ. По теореме Пифагора для прямоугольного треугольника АВС получаем АС² = АВ² – СВ². По теореме об отрезках касательной и секущей, проведенных к окружности из одной точки, получаем
АС² = СВ · СD.
Слайд 24 Таким образом, АВ² – СВ² = СВ ·
СD, 9 - СВ² = 3,2 · СВ. Решая
квадратное уравнение и учитывая, что СВ > 0, получаем СВ = 1,8. Следовательно, R = + 1,6 = 2,5.Ответ: 2,5 см.