Слайд 2
Оглавление
Введение:
Что означает геометрия
Откуда пришла геометрия
Учённые, внёсшие свой
вклад в развитие геометрии
Сочинение Евклида «Начала»
Основная часть:
Как измеряли в
древности
Начало государственного надзора за мерами в России
Метрическая система мер
Основные геометрические фигуры
Заключение
Список литературы
Слайд 3
Что означает геометрия?
Что же означает геометрия?Геометрия-это одна из
самых древних наук, она возникла очень давно, ещё до
нашей эры. В переводе с греческого слово »геометрия» означает «землемерие» ( «гео» - по-гречески земля, а «метрео» -мерить). Такое название объясняется тем, что зарождение геометрии было связанно с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, геометрия возникла на основе практической деятельности, а в дальнейшем сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур.
Слайд 4
Откуда пришла геометрия?
Первое сочинение, содержащее простейшие геометрические сведения,
дошло до нас из Древнего Египта. Оно относится к
XVII в. до н. э. В нём содержатся правила вычисления площадей и объёмов некоторых фигур и тел. Эти правила были получены практическим путём, без какого-либо логического доказательства их справедливости.
Слайд 5
Учённые, внёсшие свой вклад в развитие геометрии
Фалес
Предполагают, что

геометрию начинала Ионийская школа, а точнее, сам её основатель
— Фалес Милетский, проживший что-то около сотни лет (640–540 или 546 годы до нашей эры).
Толком мы мало что знаем о нём.
Точно известно, что имел он титул одного из семи мудрецов Греции, что по официальному счёту идёт как первый философ, первый математик, первый астроном и вообще первый по всем наукам в Греции. По-видимому, он был тем же для Греции, что Ломоносов для России.
Прокл Диддох утверждает, что Фалес доказал теоремы о равенстве вертикальных углов, о равенстве углов при основании равнобедренного треугольника, о том, что диаметр делит круг пополам и ещё ряд других.
Допустив даже, что все историки писали сущую истину, мы не можем сказать, самостоятельно ли Фалес пришёл к этим теоремам или просто пересказал идеи египтян.
По-видимому, единственный бесспорный факт из его научной деятельности — предсказание солнечного затмения 585 года до нашей эры. Но легенд о Фалесе ходило множество, и это само по себе доказывает, что учёный он был крупный.
Слайд 6
Пифагор
В современном мире Пифагор считается великим математиком и

космологом древности, однако ранние свидетельства до iii в. до н.
э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев.»
Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Такое мнение основывается на сведениях Аполлодора-исчислителя (личность не известна) и на стихотворных строках (источник стихов не известен):
«В день, когда Пифагор открыл свой чертёж знаменитый,
Славную он за него жертву быками воздвиг.»
Современные историки предполагают, что Пифагор не доказывал теорему, но мог передать грекам это знание, известное в Вавилоне за 1000 лет до Пифагора (согласно вавилонским глиняным табличкам с записями математических уравнений). Хотя сомнение в авторстве Пифагора существует, но весомых аргументов, чтобы это оспорить, нет.
Слайд 7
Платон
Платон, живший в 428–348 годах до нашей эры,

считается одним из величайших философов Греции. Геометрия ко времени
Платона уже была очень развита. Было решено много весьма и весьма сложных задач, доказаны сложнейшие теоремы. Но ясной позиции во взглядах на общую схему построения науки ещё не было. Развитие геометрии, как нередко бывает в науке, стимулировалось задачами, решения которых никак не удавалось отыскать. Требовалось при помощи циркуля и линейки, не привлекая никаких других геометрических инструментов:
разделить данный угол на три равных части (трисекция угла);
построить квадрат с площадью, равной площади данного круга (квадратура круга);
построить куб с объёмом, в два раза большим объёма данного куба (делосская задача).
Только в конце прошлого века было доказано, что в такой постановке ни одна из этих задач не может быть решена, хотя, если использовать другие геометрические инструменты, то все три задачи легко решаются.
Однако принятые у греков правила игры не позволяли пользоваться при решении задач ничем, кроме циркуля и линейки. Так что ни одна из проблем решена не была, но по ходу дела геометрия была основательно разработана. Платон очень много сделал для развития математики и весьма ценил её. На входе в его академию был даже высечен весьма категорический лозунг: «Да не войдёт сюда тот, кто не знает геометрии». Дело в том, что Платон полагал: «Изучение геометрии приближает к бессмертным богам» — и воспитывал в этом духе своих учеников, приплетая математику к месту и не к месту.
По-видимому, Платон первый чётко потребовал: математика вообще и геометрия в частности должны быть построены дедуктивным образом. Иначе говоря, все утверждения (теоремы) должны строго логически выводиться из небольшого числа основных положений — аксиом. Такая постановка — крупнейший шаг вперёд.
Слайд 8
Евклид
К IV–III векам до нашей эры геометрия

вполне оформилась как наука. Были устоявшиеся традиции, детально разработанные
методы решения задач, крупные достижения, было уже несколько учебников и различные научные школы.
О самом Евклиде практически ничего не известно.
Легенды, конечно же, имеются. Рассказывают, например, что Птолемей поначалу сам захотел одолеть премудрости геометрии, но довольно скоро обнаружил , что изучение математики требует некоторых усилий. Тогда он призвал Евклида и вопросил его, полагаю, как джентльмен джентльмена, нельзя ли постигнуть все тайны науки как-нибудь попроще? На что Евклид ответил: «В геометрии нет царского пути». Остаётся неведомым, продолжал ли после этого царь занятия математикой (вероятнее всего, он утешился в занятиях, более приличествующих царям, — таких, как приёмы, охота, пиры).
Рассказывают также, что однажды к Евклиду явился изучать геометрию некий молодой прагматик. Первый вопрос, который он задал будущему учителю, был следующий: какая практическая польза будет от штудирования «Начал»? Тогда Евклид, весьма и весьма задетый, призвал раба и сказал: «Дай ему обол (грош), он ищет выгоды, а не знаний».
Надо, впрочем, сознаться, что обе истории столь традиционны, учитывая представление древних греков о мудрецах и о математике, что особо доверять им не приходится. «Точные» же биографические данные основываются на заметках неизвестного арабского математика XII века:«Евклид, сын Наукрата, сына Зенарха, известный под именем Геометра, учёный старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира...»
Слайд 9
Сочинение Евклида «Начала»
Более двух тысяч лет она была

главным и практически единственным руководством по геометрии для учёных
как западного, так и восточного мира. Ещё в конце XIX столетия во многих английских школах геометрию изучали по адаптированному изданию «Начал», и вряд ли можно найти более выразительное свидетельство популярности. Основа «Начал» — строгая и жёсткая логика, точнее, Евклид всё время стремится к таковой. Можно полагать, что он был последователем Платона и Аристотеля. А Платон, как вы помните, требовал строго дедуктивного построения математики.
В фундаменте — аксиомы, основные положения, принимаемые без доказательства, а далее всё должно быть строго логично выведено из аксиом. Этот идеал и пытается осуществить Евклид.
С современных позиций буквально вся его аксиоматика неудовлетворительна. Но это легко заявлять сейчас, после 25 веков исследований. А в своё время логика Евклида оставляла совершенно подавляющее впечатление. Во всяком случае, не следует забывать, что сама логическая схема её стала с тех пор канонической для построения любого раздела математики.
Попытки изложить геометрию на основе аксиоматического метода были и до Евклида. Но можно уверенно заключить, что работа Евклида была наиболее удачной. Свидетельство тому — необычайная известность его книги уже в древнем мире, благодаря которой она и дошла до нас.
«Начала» блестяще написаны, в них чувствуется мастер своего дела, тонкий учёный и великолепный педагог. Поэтому поголовное поклонение математиков Евклиду и его «Началам» понятно и оправданно. Добавим ещё, что эта книга обратила в математическую веру несколько десятков молодых людей, ставших впоследствии крупнейшими математиками мира.
Влияние Евклида было поразительно во все века во всех краях света.
Слайд 10
Н. И. Лобачевский
Четвёртый период в развитии геометрии открывается

построением
Н. И. Лобачевским новой, неевклидовой геометрии, называемой теперь геометрией Лобачевского. Первая работа Лобачевского в этом направлении была доложена им на заседании физико-математического факультета Казанского университета в 1826 г. и опубликована в развитой форме в 1829 г.
Источник, сущность и значение идей Лобачевского сводятся к следующему. В геометрии Евклида имеется аксиома о параллельных, утверждающая: «через точку, не лежащую на данной прямой, можно провести не более чем одну прямую, параллельную данной». Многие геометры пытались доказать эту аксиому, исходя из других основных посылок геометрии, но безуспешно. Лобачевский пришёл к мысли, что такое доказательство невозможно.
Утверждение, противоположное аксиоме Евклида, будет: «через точку, не лежащую на данной прямой, можно провести не одну, а по крайней мере две параллельные ей прямые». Это и есть аксиома Лобачевского.
По мысли Лобачевского, присоединение этого положения к другим основным положениям геометрии не должно приводить к противоречию, т. е. все выводы, получаемые на основе такого соединения, будут логически безупречными.
Система этих выводов и образует новую, неевклидову геометрию.
Заслуга Лобачевского состоит в том, что он не только высказал эту идею, но действительно построил и всесторонне развил эту новую геометрию, логически столь же совершенную и богатую выводами, как евклидова, несмотря на её несоответствие обычным наглядным представлениям. Лобачевский рассматривал свою геометрию как возможную теорию пространственных отношений; однако она оставалась гипотетической до 1868—1870 гг., когда был выяснен её реальный смысл и тем самым было дано её полное обоснование.
Переворот в геометрии, произведённый Лобачевским, по своему значению не уступает ни одному из переворотов в естествознании, и недаром Лобачевский был назван «Коперником геометрии».
«Напрасное старание со времен Евклида, в продолжение двух тысяч лет, — писал он, — заставило меня подозревать, что в самых понятиях еще не заключается той истины, которую хотели доказывать и в которую поверить, подобно другим физическим законам, могут лишь опыты, каковы, например, астрономические наблюдения».
Слайд 11
Как измеряли в древности?
Без измерений нельзя ни сшить
платье, ни выточить на токарном станке деталь, ни узнать
который час. В древности длины измеряли локтями, длиной ступни, длинами зёрен, а массу-массам зёрен, воды определённого объёма и т. д. Расстояния измерялись шагами. Конечно, у разных людей величина шага различна, но брали некоторую среднюю величину. В каждой стране были свои единицы измерения. В Древнем Риме для таких измерений служила миля- так называли путь в тысячу двойных шагов. Эстонские моряки мерили расстояние трубками. В Испании такой же мерой расстояния служила сигара, а в Японии- лошадиный башмак. Так называется путь, проходимый лошадью, пока износится подкова.
Слайд 12
Начало государственного надзора за мерами
В дореволюционных книгах

часто встречаются такие единицы длины, как версты, сажени, аршины,
футы. В торговле тогда применяли пуды, фунты, золотники.
Русский народ создал свою собственную систему мер. Памятники X века говорят не только о существовании системы мер в Киевской Руси, но и государственном надзоре за их правильностью. Надзор этот был возложен на духовенство. В одном из уставов князя Владимира Святославовича говорится: «…издавна установлено и поручено епископам наблюдать за правильностью мер… не допускать ни умаления, ни увеличения их…» Вызвана была эта необходимость надзора потребностями торговли как внутри страны, так со странами Запада (Византия, Рим, позднее германские города) и Востока (Средняя Азия, Персия, Индия). На церковной площади происходили базары, в церкви стояли лари для хранения договоров по торговым сделкам, при церквах стояли верные весы и меры, в подвалах церквей хранились товары. Взвешивания производились в присутствии представителей духовенства.
Слайд 13
Метрическая система мер
Двести лет тому назад в разных
странах применялись различные единицы измерения длин, площадей, масс и
т. Д. Эти единицы оказались не согласованными друг с другом. Во время Французской революции была разработана метрическая система мер, оказавшаяся самой простой и удобной. Во внедрении этой системы мер в практику большую роль сыграли русские учённые.
Слайд 14
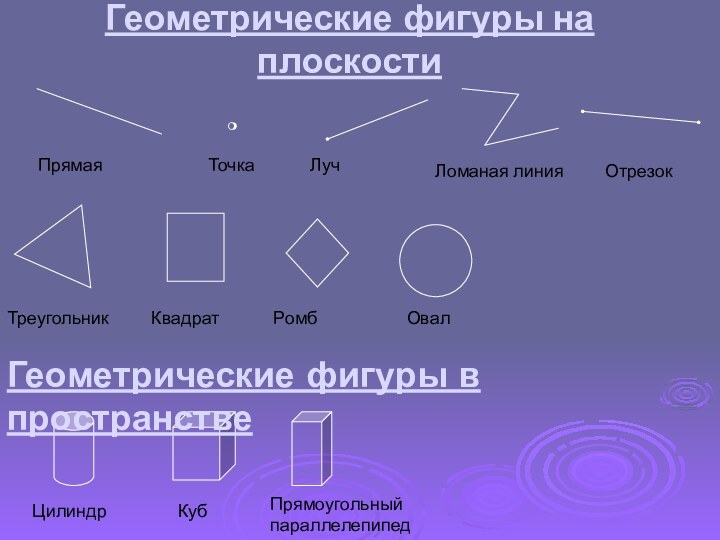
Геометрические фигуры на плоскости
Прямая
Луч
Отрезок
.
Точка
Ломаная линия
Треугольник
Квадрат
Ромб
Овал
Цилиндр
Куб
Геометрические фигуры в пространстве
Прямоугольный параллелепипед
Слайд 15
Заключение
Для современной геометрии характерно ещё большее, чем прежде,

проникновение её идей и методов в другие области математики
и обратно, так что точное выделение геометрии из всей математики оказывается, по существу, невозможным. Существенно изменилось также отношение геометрии к изучению материальной действительности: если раньше геометрия была лишь теорией пространственных отношений и форм, основанной на положениях, сформулированных у Евклида, то теперь она стала также наукой о формах и отношениях действительности, сходных с пространственными. Область её применения к исследованию природы чрезвычайно расширилась. Но при всём разнообразии приложений и абстрактности теорий современной геометрии все они имеют общий источник в изучении конкретных пространственных форм и отношений, которое было впервые суммировано в элементарной евклидовой геометрии и из которого, в конечном счёте, исходят все понятия геометрии. Это единство источника позволяет дать определение геометрии как той части математики, которая развилась из изучения пространственных форм и отношений.