Презентация на тему Определение компланарных векторов

Содержание

2. Цели урокаВвести определение компланарных векторов.Рассмотреть признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.
3. Фронтальный опросЧто называется вектором в пространстве? Как
4. 8. Справедливо ли утверждение:Любые два противоположно направленных
5. 9. Может ли длина суммы двух векторов
6. Новый материалОпределение.Векторы называются компланарными, если при откладывании
7. Новый материалУстное решение № 355
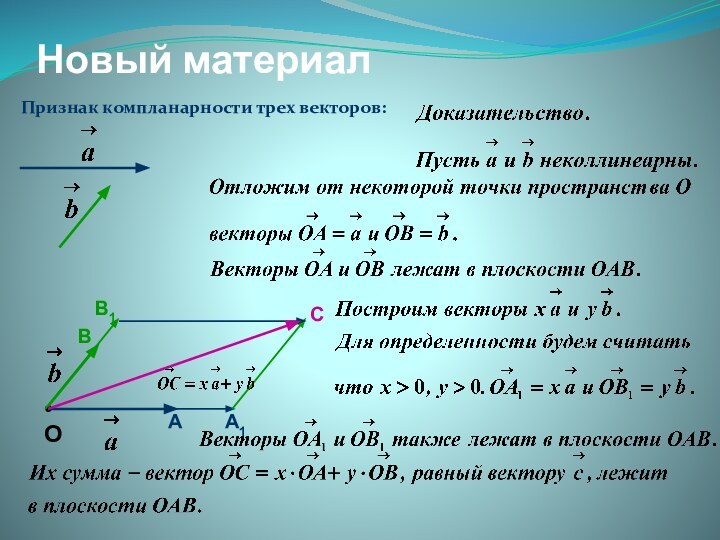
8. Новый материалПризнак компланарности трех векторов:
9. Новый материалПризнак компланарности трех векторов:•ОА1В1С
10. Новый материал
11. Новый материалОпределение.Утверждение, обратное признаку компланарности векторов:Докажем это.
12. Новый материалОАВРР1Так как векторы компланарны, то они лежат в одной плоскости.
13. Новый материалМы умеем на плоскости складывать векторы
14. Новый материалОпределение.
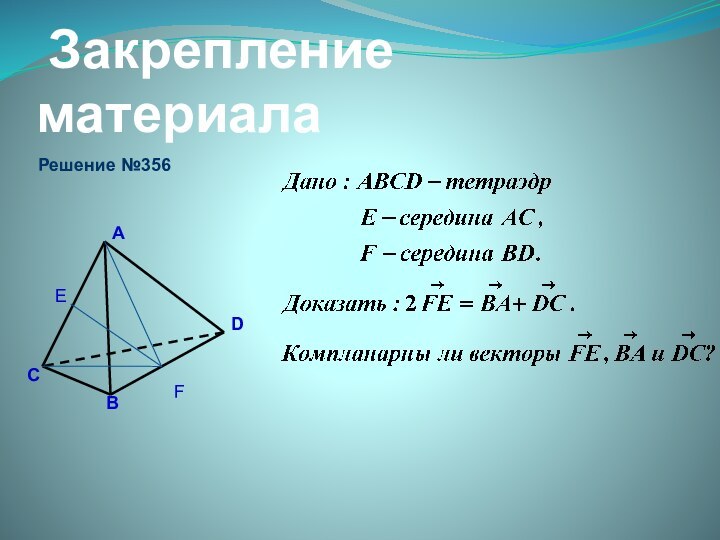
15. Закрепление материалаРешение №356EF
16. Закрепление материала№356FE
17. Скачать презентацию
18. Похожие презентации

Цели урокаВвести определение компланарных векторов.Рассмотреть признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.

Главная
Геометрия
Определение компланарных векторов

Компланарные векторыПодготовила учитель математикиБаландина Наталья Михайловна

Цели урокаВвести определение компланарных векторов.Рассмотреть признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.

Фронтальный опросЧто называется вектором в пространстве? Как обозначается вектор?Что называется длиной вектора?

8. Справедливо ли утверждение:Любые два противоположно направленных вектора коллинеарныЛюбые два коллинеарных вектора

9. Может ли длина суммы двух векторов быть меньше длины каждого из

Новый материалОпределение.Векторы называются компланарными, если при откладывании от одной и той же

Новый материалПризнак компланарности трех векторов:

Новый материалПризнак компланарности трех векторов:•ОА1В1С

Новый материалОпределение.Утверждение, обратное признаку компланарности векторов:Докажем это.

Новый материалОАВРР1Так как векторы компланарны, то они лежат в одной плоскости.

Новый материалМы умеем на плоскости складывать векторы по правилу треугольника и параллелограмма.

Домашнее заданиеп. 39, 40вопросы 13-15 стр. 97№358, разобрать №366, 368(а, б)

Слайды презентации

Слайд 2 Цели урока
Ввести определение компланарных векторов.
Рассмотреть признак компланарности трех

векторов и правило параллелепипеда, сложение трех некомпланарных векторов.

Слайд 3 Фронтальный опрос
Что называется вектором в пространстве? Как обозначается

Фронтальный опросЧто называется вектором в пространстве? Как обозначается вектор?Что называется длиной

вектор?
Что называется длиной вектора? Как она обозначается?
Какой вектор называется

нулевым? Как он обозначается?
Какие векторы называются коллинеарными?
Какие векторы называются сонаправленными? Как они обозначаются?
Какие векторы называются противоположнонавленными? Как они обозначаются?
Какие векторы называются равными?

Слайд 4 8. Справедливо ли утверждение:
Любые два противоположно направленных вектора

8. Справедливо ли утверждение:Любые два противоположно направленных вектора коллинеарныЛюбые два коллинеарных

коллинеарны
Любые два коллинеарных вектора сонаправлены
Любые два равных вектора коллинеарны
Любые

два сонаправленных вектора равны

Слайд 5 9. Может ли длина суммы двух векторов быть

9. Может ли длина суммы двух векторов быть меньше длины каждого

меньше длины каждого из слагаемых?
10. Может ли длина суммы

нескольких ненулевых векторов быть равной сумме длин этих векторов?
11. Может ли длина разности двух ненулевых векторов быть равной сумме длин этих векторов?
12. Может ли длина разности двух ненулевых векторов быть равной длине разности этих векторов?
13. Может ли длина суммы двух ненулевых векторов быть равна длине разности этих векторов?

Слайд 6 Новый материал
Определение.
Векторы называются компланарными, если при откладывании от

Новый материалОпределение.Векторы называются компланарными, если при откладывании от одной и той

одной и той же точки они будут лежать в

одной плоскости.
Иначе: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Почему?
Три произвольных вектора могут быть как компланарными, так и некомпланарными.