Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Площадь квадрата

Содержание

2. Площадь — численная характеристика двумерной (плоской или искривлённой)
3. Аксиомы площади Площадь единичного квадрата равна 1.Площадь
4. Докажем, что площадь квадрата со стороной а
5. Сторона каждого маленького квадрата равна…, т.е. равна
6. При этом каждая сторона данного квадрата разобьется
7. Следовательно, площадь данного квадрата равна
8. Площадь данного квадрата заключена между площадью квадрата
9. Будем неограниченно увеличивать число n. Тогда число
10. Теорема Пифагора. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
11. ФормулировкиГеометрическая формулировка:Изначально теорема была сформулирована следующим образом:В
12. Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины
13. Обе формулировки теоремы эквивалентны, но вторая формулировка
14. Скачать презентацию
15. Похожие презентации

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры, неформально говоря, показывающая размер этой фигуры.Фигуры с одинаковой площадью называются равновеликими.

Площадь квадратаПрезентация по геометрии ученицы 8 «В» класса Жиряковой Марии.

Аксиомы площади Площадь единичного квадрата равна 1.Площадь аддитивна.Площадь неотрицательна.аддитивность площади означает, что

Докажем, что площадь квадрата со стороной а равна а2.1 случай.а=1/n, где n-

Сторона каждого маленького квадрата равна…, т.е. равна а. Итак, S= 1/n2 =

При этом каждая сторона данного квадрата разобьется на m равных частей, и,

Следовательно, площадь данного квадрата равна m2 * (1/10n)2 =(m/10n)2= (a*10n/10n)2=

Площадь данного квадрата заключена между площадью квадрата со стороной аn и площадью

Будем неограниченно увеличивать число n. Тогда число 1/10n , будет становиться сколь

Теорема Пифагора. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

ФормулировкиГеометрическая формулировка:Изначально теорема была сформулирована следующим образом:В прямоугольном треугольнике площадь квадрата, построенного

Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин

Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует

ДоказательстваПо преданию, Пифагор отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях

Слайды презентации

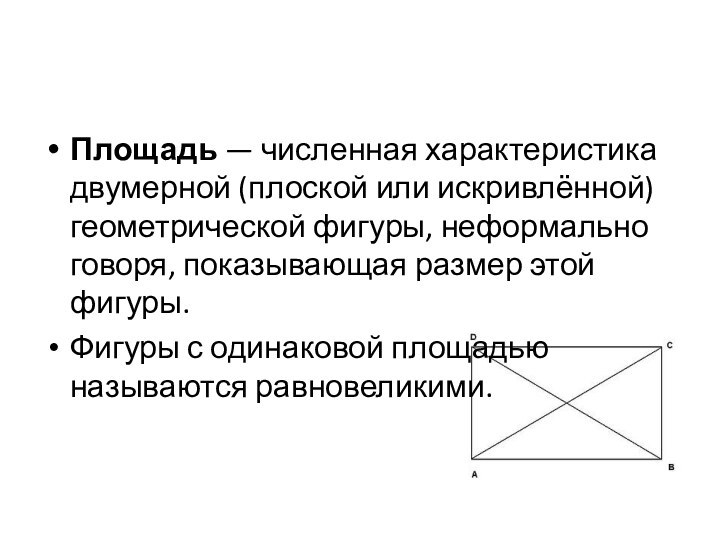
Слайд 2 Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры, неформально говоря,

фигуры, неформально говоря, показывающая размер этой фигуры.
Фигуры с одинаковой

площадью называются равновеликими.

Слайд 3 Аксиомы площади
Площадь единичного квадрата равна 1.
Площадь аддитивна.
Площадь неотрицательна.

аддитивность

Аксиомы площади Площадь единичного квадрата равна 1.Площадь аддитивна.Площадь неотрицательна.аддитивность площади означает,

площади означает, что площадь целого равен сумме …составляющих его

частей.

Слайд 4 Докажем, что площадь квадрата со стороной а равна

Докажем, что площадь квадрата со стороной а равна а2.1 случай.а=1/n, где

а2.
1 случай.
а=1/n, где n- нат.число. Возьмем квадрат со стороной

1 и разобьем его на n2 равных квадратов, как на рисунке.
Так как площадь большого
квадрата равна 1, то площадь
каждого маленького
квадрата...

Слайд 5 Сторона каждого маленького квадрата равна…, т.е. равна а.

Итак, S= 1/n2 = (1/n)2 =a2 (1)
Случай 2.

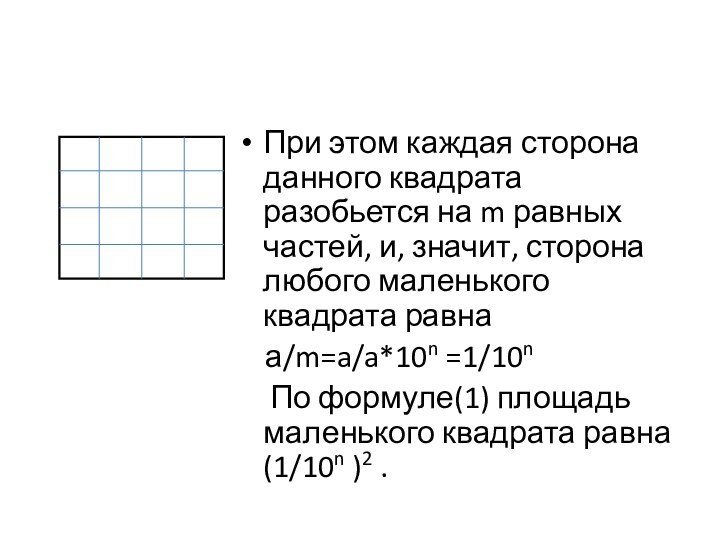
Пусть теперь а представляет собой конечную десятичную дробь, содержащую n знаков после запятой, так же число а может быть целым, и тогда n=0. Тогда число квадратиков на каждой стороне m=а*10n . Разобьем данный квадрат со стороной а на m2 равных квадратов, как на рисунке.

Слайд 6 При этом каждая сторона данного квадрата разобьется на

При этом каждая сторона данного квадрата разобьется на m равных частей,

m равных частей, и, значит, сторона любого маленького квадрата

равна
а/m=a/a*10n =1/10n
По формуле(1) площадь маленького квадрата равна (1/10n )2 .

Слайд 7 Следовательно, площадь данного квадрата равна
m2

* (1/10n)2 =(m/10n)2= (a*10n/10n)2= a2 .
Пусть число а представляет

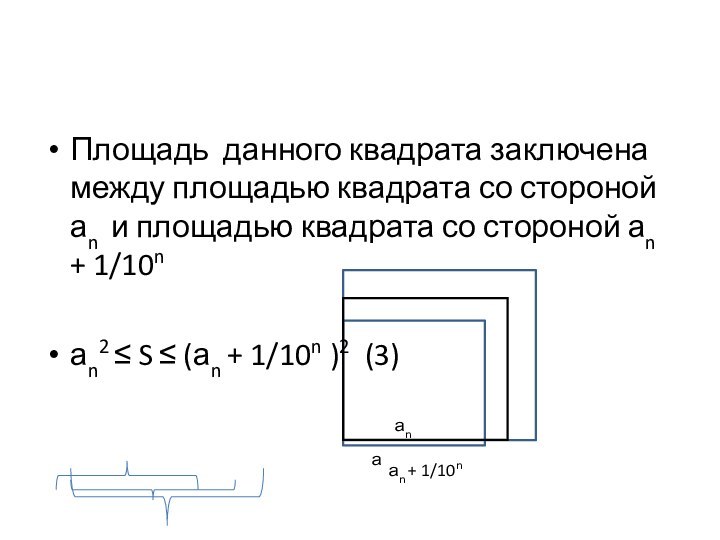
собой бесконечную десятичную дробь. Рассмотрим число аn, получаемое из а отбрасыванием всех десятичных знаков после запятой, начиная с(n+1)-го. Так как число а отличается от аn не более чем на 1/10n, то аn ≤ а ≤ аn + 1/10n , откуда аn2 ≤ а2 ≤ (аn + 1/10n )2 . (2)

Слайд 8 Площадь данного квадрата заключена между площадью квадрата со

Площадь данного квадрата заключена между площадью квадрата со стороной аn и

стороной аn и площадью квадрата со стороной аn +

1/10n

аn2 ≤ S ≤ (аn + 1/10n )2 (3)

аn + 1/10n

аn

Слайд 9 Будем неограниченно увеличивать число n. Тогда число 1/10n

Будем неограниченно увеличивать число n. Тогда число 1/10n , будет становиться

, будет становиться сколь угодно малым, и, значит, число

(аn + 1/10n )2 будет сколь угодно мало отличаться от числа аn2 . Поэтому из неравенств (2) и (3) следует, что число S сколь угодно мало отличается от числа а2 . Следовательно, эти числа равны: S= а2 , Ч.Т.Д.

Слайд 10 Теорема Пифагора.
Теорема Пифагора — одна из основополагающих теорем

евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Слайд 11 Формулировки
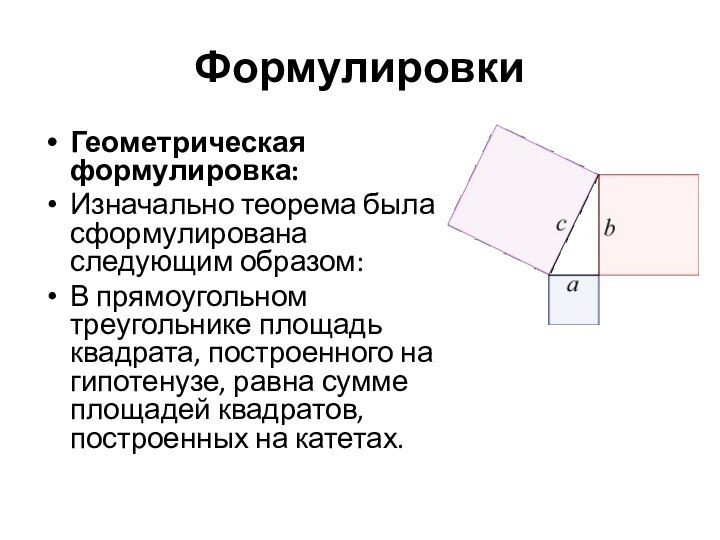
Геометрическая формулировка:
Изначально теорема была сформулирована следующим образом:
В прямоугольном

треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей

квадратов, построенных на катетах.

Слайд 12 Алгебраическая формулировка:
В прямоугольном треугольнике квадрат длины гипотенузы равен

Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов

сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника

через c, а длины катетов через a и b:

Слайд 13 Обе формулировки теоремы эквивалентны, но вторая формулировка более

Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не

элементарна, она не требует понятия площади. То есть второе

утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора:
Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.