Презентация на тему по математике на тему Призма, виды призм.

плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным

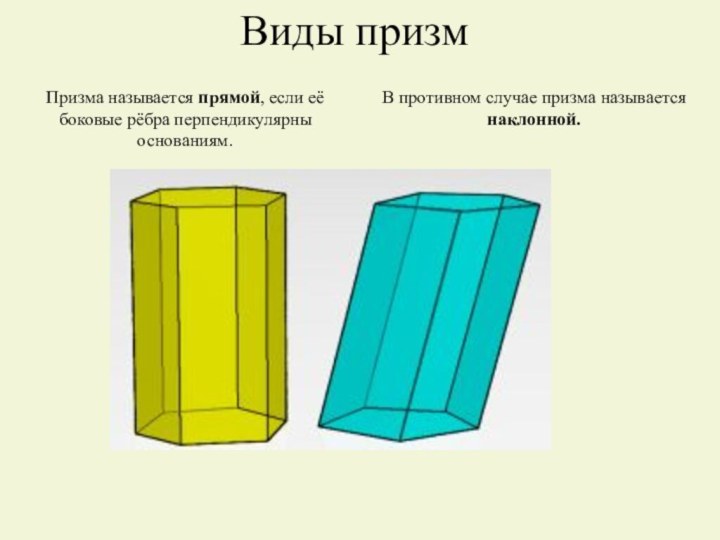
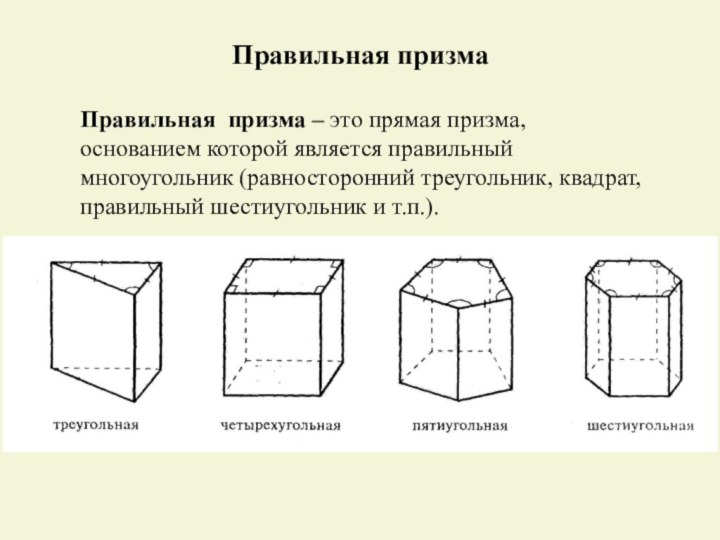
переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.

Многоугольники называются основаниями призмы.

Отрезки, соединяющие соответствующие вершины, -боковыми рёбрами призмы.

Боковой гранью призмы называются все грани, кроме её оснований.

сумма площадей боковых граней.

Полная поверхность призмы равна сумме поверхности

и площадей оснований.

плоскостях.
Боковые ребра призмы параллельны и равны.
У параллелепипеда противолежащие грани

равны и параллельны.
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Площадь боковой поверхности призмы S=Pl, где — P периметр основания, l — высота призмы (длина бокового ребра).
Точка пересечения диагоналей параллелепипеда является центром симметрии.
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений.

перпендикулярны основаниям.
В противном случае призма называется наклонной.

(равносильно) многогранник, у которого шесть граней и каждая из

них — параллелограмм.

Куб (частный случай параллелепипеда и призмы)— правильный многогранник, каждая грань которого представляет собой квадрат.

Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом.

является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и

т.п.).

Правильная призма