- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Модуль
Содержание
- 2. Модуль «ГЕОМЕТРИЯ» №10Повторение (2)Ответ: 4.Найти АС.В С А 5 ⇒ ⇒ По теореме Пифагора
- 3. ПовторениеКосинус острого угла прямоугольного треугольника равен отношению
- 4. Модуль «ГЕОМЕТРИЯ» №10Повторение (2)Ответ: 17.Найти АВ.В С А 15 ⇒ ⇒ По теореме Пифагора
- 5. ПовторениеТангенс острого угла прямоугольного треугольника равен отношению
- 6. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 52.Найти АВ.В С А 26 BH=HA, зн. АВ=2 AH.H ⇒ HA=СH=26.АВ=2 ∙26=52.
- 7. ПовторениеВысота в равнобедренном треугольнике, проведенная к основанию,
- 8. Модуль «ГЕОМЕТРИЯ» №10Повторение (2)Ответ: 117.Найти CH.В А
- 9. ПовторениеВысота в равнобедренном треугольнике, проведенная к основанию,
- 10. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 75.Найти AB.В А
- 11. ПовторениеВысота в прямоугольном треугольнике, проведенная к основанию
- 12. Модуль «ГЕОМЕТРИЯ» №10Повторение (4)Ответ: 5.Дано: параллелограмм, P=10,АЕ:ЕD=1:3.Найти
- 13. ПовторениеБиссектриса – это луч, который делит угол
- 14. Модуль «ГЕОМЕТРИЯ» №10Повторение (2)Ответ: 66.АВСD – прямоугольник,
- 15. ПовторениеПрямоугольник – это параллелограмм с прямыми угламиКатет, лежащий против угла в 30⁰, равен половине гипотенузы
- 16. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 52. АВСD параллелограмм.
- 17. ПовторениеЕсли две параллельные прямые пересечены третьей, то
- 18. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 49.АВСD – ромб.
- 19. ПовторениеДиагонали ромба пересекаются под прямым углом и
- 20. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 22.В А D
- 21. ПовторениеСредняя линия трапеции – это отрезок, соединяющий
- 22. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 103.АВСD – трапеция,
- 23. ПовторениеЕсли в четырехугольнике противоположные стороны параллельны, то
- 24. Модуль «ГЕОМЕТРИЯ» №10Повторение (2)Ответ: 37.АВСD – трапецияВ А D С 29 21 М К ?
- 25. ПовторениеСредняя линия трапеции – это отрезок, соединяющий
- 26. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 94.АВСD – трапецияНайти
- 27. ПовторениеЕсли гипотенуза и катет одного прямоугольного треугольника
- 28. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 9,5.E,F – середины
- 29. ПовторениеСредняя линия трапеции равна полусумме оснований трапецииСредняя
- 30. Модуль «ГЕОМЕТРИЯ» №10Повторение (2)Ответ: 13.АВСD – трапеция,АВ=23, CD=3.Найти МК.В А D С М К AD+BC=AB+CD=23+3=26⇒
- 31. ПовторениеЕсли в четырехугольник можно вписать окружность, то
- 32. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 2,5.АВСD – трапеция,
- 33. ПовторениеЕсли в четырехугольник можно вписать окружность, то
- 34. Модуль «ГЕОМЕТРИЯ» №10Повторение (4)Ответ: 22,5.АВСD – ромб.Найти
- 35. ПовторениеРадиус окружности, проведенный в точку касания перпендикулярен
- 36. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 8.Найти r.В А С r11 По теореме Пифагора в ∆BCH r=½d=½АВ=½∙16=8
- 37. ПовторениеПрямой угол, вписанный в окружность опирается на
- 38. Модуль «ГЕОМЕТРИЯ» №10Повторение (3)Ответ: 6.АВСD – трапеция,
- 39. ПовторениеСредняя линия трапеции равна полусумме оснований трапецииОписать
- 40. Скачать презентацию
- 41. Похожие презентации







































Слайд 3
Повторение
Косинус острого угла прямоугольного треугольника равен отношению прилежащего
катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов
Слайд 5
Повторение
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего
катета к прилежащему
В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов
Слайд 6
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 52.
Найти АВ.
В
С
А
26
BH=HA, зн. АВ=2 AH.
H
⇒
HA=СH=26.
АВ=2 ∙26=52.
Слайд 7
Повторение
Высота в равнобедренном треугольнике, проведенная к основанию, является
и медианой
В прямоугольном треугольнике сумма острых углов равна 90⁰
Если
в треугольнике два угла равны, то такой треугольник равнобедренный
Слайд 8
Модуль «ГЕОМЕТРИЯ» №10
Повторение (2)
Ответ: 117.
Найти CH.
В
А
H
С
BH=HA, зн. АH=½ AB=
По теореме Пифагора в ∆ACH
Слайд 9
Повторение
Высота в равнобедренном треугольнике, проведенная к основанию, является
и медианой
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов
Слайд 10
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 75.
Найти AB.
В
А
H
С
120⁰
Проведем высоту CH, получим ∆ВCH.
∠ВCH=60⁰
⇒
∠CВH=30⁰
⇒
По теореме Пифагора в ∆BCH
Слайд 11
Повторение
Высота в прямоугольном треугольнике, проведенная к основанию является
биссектрисой и медианой
В прямоугольном треугольнике катет, лежащий против угла
в 30⁰, равен половине гипотенузыВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 12
Модуль «ГЕОМЕТРИЯ» №10
Повторение (4)
Ответ: 5.
Дано: параллелограмм, P=10,
АЕ:ЕD=1:3.
Найти AD
В
А
D
С
Е
1
2
3
∠1=∠3 как
накрест лежащие при секущей ВЕ ∠3=∠2 так как ∠1=∠2 по условию
⇒
АВ=АЕ
Пусть АЕ=х,
тогда АВ=х, ЕD=3х
Р=2∙(х+3х)
⇒
2∙(х+3х)=10
4х=5
Х=1,25
AD=4∙1,25=5
Слайд 13
Повторение
Биссектриса – это луч, который делит угол пополам
Периметр
многоугольника – это сумма длин всех сторон многоугольника
При пересечении
двух параллельных прямых накрест лежащие углы равныЕсли два угла в треугольнике равны, то треугольник - равнобедренный
Слайд 14
Модуль «ГЕОМЕТРИЯ» №10
Повторение (2)
Ответ: 66.
АВСD – прямоугольник, ∠1:∠2=1:2.
Найти
АС.
В
А
D
С
33
1
2
∠1=⅓ ∠ВАС
⇒
∠1=⅓ ∙90⁰=30⁰
⇒
СD=½АС
⇒
АС=2 СD= 66
Слайд 15
Повторение
Прямоугольник – это параллелограмм с прямыми углами
Катет, лежащий
против угла в 30⁰, равен половине гипотенузы
Слайд 16
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 52.
АВСD параллелограмм.
Найти
большую сторону
2
3
4
1
26
В
А
D
С
∠2=∠5 как накрест лежащие при сек. DЕ
∠4=∠6 как накрест лежащие при сек. АЕ
⇒
DC=ЕC
Е
6
5
⇒
⇒
∠1=∠5
АВ=ВЕ
⇒
∠3=∠6
DC=ВЕ=ЕС=26
⇒
Так как АВ=СD
ВC=ВЕ+ЕС=26+26=52
Слайд 17
Повторение
Если две параллельные прямые пересечены третьей, то накрест
лежащие углы равны
Если в треугольнике два угла равны, то
треугольник равнобедренныйЕсли отрезок точкой разделен на части, то его длина равна сумме его частей
Слайд 18
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 49.
АВСD – ромб. Найти
меньшую диагональ.
В
А
D
С
49
60⁰
О
В
∆АОВ, где ∠ВАО=30⁰⇒
ОВ=½АВ=½∙49=24,5
ВD=2ОВ=2∙24,5=49
Слайд 19
Повторение
Диагонали ромба пересекаются под прямым углом и делят
углы ромба пополам
Катет прямоугольного треугольника, лежащий против угла в
30⁰ равен половине гипотенузыДиагонали параллелограмма (ромба) точкой пересечения делятся пополам
Слайд 20
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 22.
В
А
D
С
44
12
М
К
Е
?
По теореме Фалеса
АЕ=ЕС⇒
ЕК – средняя линия ∆АСD
⇒
ЕК=½АD=½∙44=22
Слайд 21
Повторение
Средняя линия трапеции – это отрезок, соединяющий середины
боковых сторон трапеции
Параллельные прямые, проведенные через концы равных отрезков
на одной из сторон угла, отсекают равные отрезки на другой стороне углаСредняя линия треугольника равна половине третьей стороны треугольника
Слайд 22
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 103.
АВСD – трапеция, СЕ||АВ.
P∆CDЕ =69. Найти P трапеции
В
А
D
С
34
Е
Так как СЕ||АВ, то АВ=ЕС, АЕ=ВС=34
АD=АЕ+ЕD
P∆CDЕ =CD+ЕD+СЕ
P∆АВCD =АВ+ВС+CD+АD
⇒
P∆АВCD =P∆CDЕ +ВС=69+34=103
Слайд 23
Повторение
Если в четырехугольнике противоположные стороны параллельны, то такой
четырехугольник - параллелограмм
В параллелограмме противоположные стороны равны
Если отрезок точкой
разделен на части, то его длина равна сумме его частей
Слайд 25
Повторение
Средняя линия трапеции – это отрезок, соединяющий середины
боковых сторон трапеции
Средняя линия трапеции равна полусумме оснований трапеции
Слайд 26
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 94.
АВСD – трапеция
Найти среднюю
линию трапеции
В
А
D
С
94
51
H
?
К
М
Проведем СЕ⍊AD, получим ∆ABH=∆CED и прямоугольник BCEH
⇒
AD=AH+HE+ЕD=
E
51+94=145
⇒
AH=ЕD=51,
BC=HE=HD-ED=94-51=43,
⇒
Слайд 27
Повторение
Если гипотенуза и катет одного прямоугольного треугольника соответственно
равны гипотенузе и катету другого треугольника, то треугольники равны
Если
отрезок точкой разделен на части, то его длина равна сумме длин его частейСредняя линия трапеции равна полусумме оснований трапеции
Слайд 28
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 9,5.
E,F – середины диагоналей.
Найти
EF.
В
А
D
С
34
15
М
К
Е
F
⇒
ME и FK средние линии ∆ABС=∆DВС с общей стороной ВС
ME=FK=½BC=½∙15=7,5
EF=MK-ME-FK=24,5-7,5-7,5=9,5
Слайд 29
Повторение
Средняя линия трапеции равна полусумме оснований трапеции
Средняя линия
треугольника равна половине третьей стороны треугольника
Если отрезок точкой разделен
на части, то его длина равна сумме длин его частей
Слайд 30
Модуль «ГЕОМЕТРИЯ» №10
Повторение (2)
Ответ: 13.
АВСD – трапеция,
АВ=23, CD=3.
Найти
МК.
В
А
D
С
М
К
AD+BC=AB+CD=23+3=26
⇒
Слайд 31
Повторение
Если в четырехугольник можно вписать окружность, то суммы
противоположных сторон четырехугольника равны
Средняя линия трапеции равна полусумме оснований
трапеции
Слайд 32
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 2,5.
АВСD – трапеция, P∆ABCD
=100. Найти r.
В
А
D
С
r
45
AD+BC=AB+CD=½ P∆ABCD
=½∙100 =50AB=50-CD =50-45=5
r=½d=½AB=½∙5=2,5
Слайд 33
Повторение
Если в четырехугольник можно вписать окружность, то суммы
противоположных сторон четырехугольника равны
Радиус окружности, проведенный в точку касания
перпендикулярен касательнойРадиус окружности равен половине диаметра
Слайд 34
Модуль «ГЕОМЕТРИЯ» №10
Повторение (4)
Ответ: 22,5.
АВСD – ромб.
Найти r.
В
А
D
С
r
90
30⁰
Проведем СH⍊AD, получим прямоугольный
∆CDH H
CH=½CD=½∙90=45
r=½d=½CD=½∙45=22,5
Слайд 35
Повторение
Радиус окружности, проведенный в точку касания перпендикулярен касательной
Перпендикуляры
между параллельными прямыми равны
В прямоугольном треугольнике катет, лежащий против
угла в 30⁰ равен половине гипотенузыРадиус окружности равен половине диаметра
Слайд 36
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 8.
Найти r.
В
А
С
r
11
По теореме Пифагора в ∆BCH
r=½d=½АВ=½∙16=8
Слайд 37
Повторение
Прямой угол, вписанный в окружность опирается на диаметр
окружности
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Радиус
окружности равен половине диаметра
Слайд 38
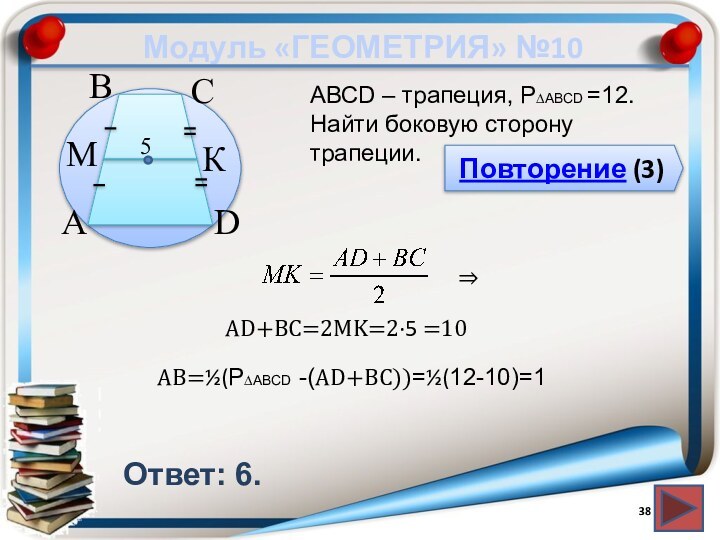
Модуль «ГЕОМЕТРИЯ» №10
Повторение (3)
Ответ: 6.
АВСD – трапеция, P∆ABCD
=12. Найти боковую сторону трапеции.
В
А
С
D
К
M
5
⇒
AD+BC=2MK=2∙5 =10
AB=½(P∆ABCD -(AD+BC))=½(12-10)=1
Слайд 39
Повторение
Средняя линия трапеции равна полусумме оснований трапеции
Описать окружность
можно только около равнобедренной трапеции
Периметр многоугольника – это сумма
длин всех сторон многоугольника





























