- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
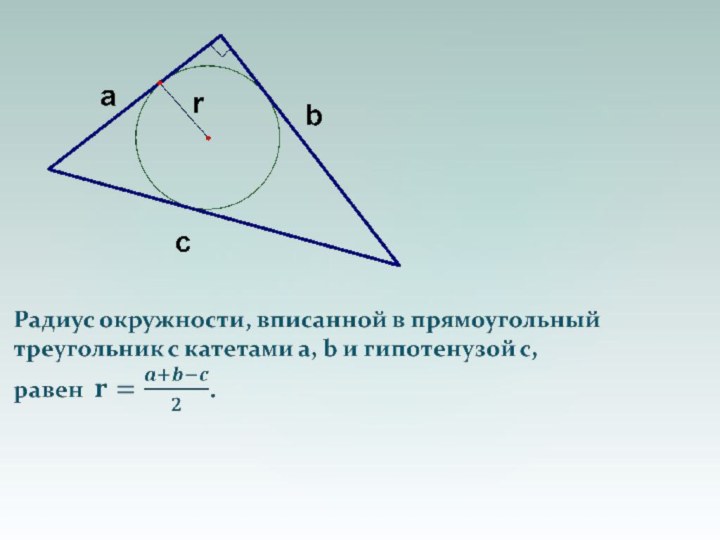
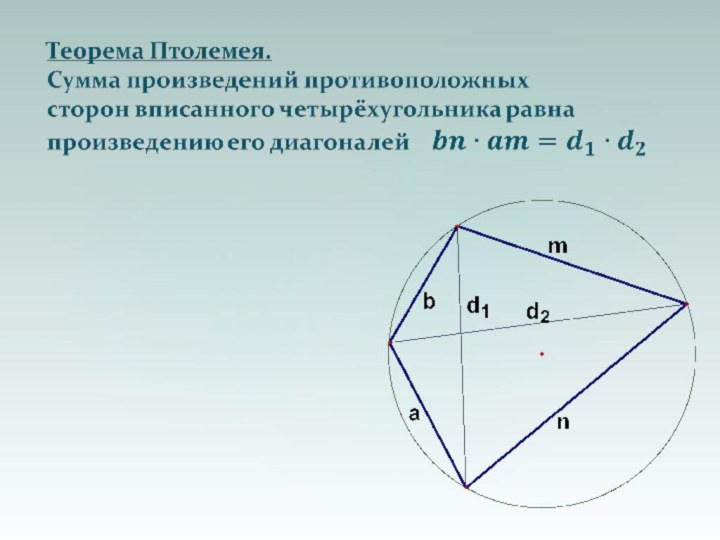
Презентация на тему по теме Полезные факты планиметрии
Содержание
- 2. Биссектрисы смежных углов перпендикулярны. Биссектрисы внутренних односторонних углов при двух параллельных прямых и секущей перпендикулярны.
- 3. а) Если медиана треугольника равна половине стороны,
- 5. Если М — точка касания со стороной
- 6. Если окружность касается основания ВС треугольника ABC
- 8. Если прямые, проходящие через точку А, касаются
- 9. Если прямая, проходящая через точку А и
- 14. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
- 15. Если сумма углов при одном из оснований
- 16. Проекция боковой стороны равнобедренной трапеции на основание
- 17. Если в трапецию можно вписать окружность, то
- 19. Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна её средней линии.
- 20. Замечательное свойство трапеции. а) Точка пересечения диагоналей
- 21. Отрезок прямой, параллельной основаниям трапеции, заключённый внутри
- 24. Площадь четырёхугольника с перпендикулярными диагоналями равна половине произведения диагоналей.
- 25. Площадь любого четырёхугольника равна половине произведения диагоналей на синус угла между ними.
- 27. Середины двух противоположных сторон любого четырёхугольника и
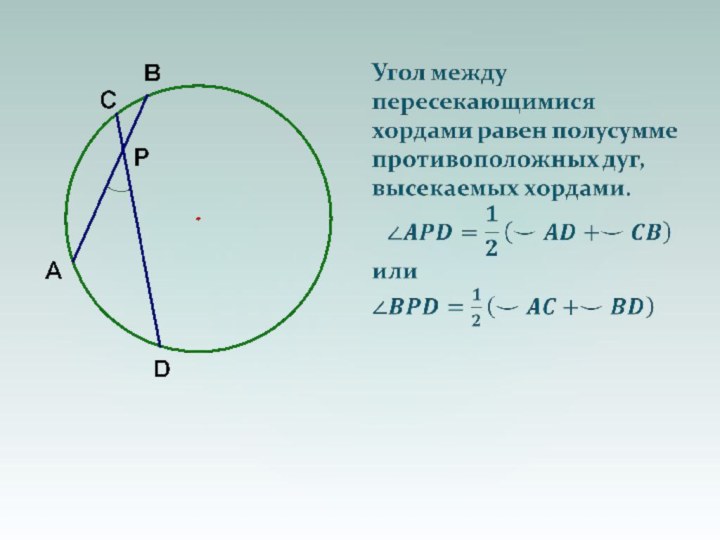
- 30. а) Диаметр, перпендикулярный хорде, делит её пополам.
- 31. Как это работает…
- 35. Геометрическое место точек, из которых отрезок АВ
- 36. а) Линия центров двух пересекающихся окружностей перпендикулярна
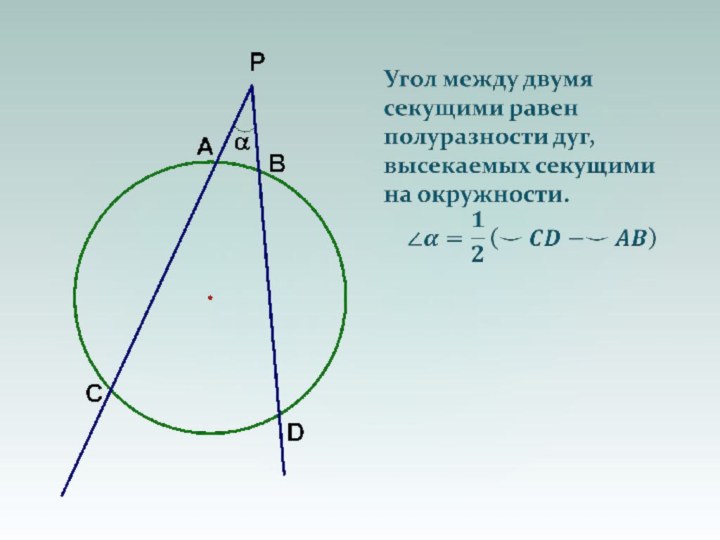
- 40. Прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним.
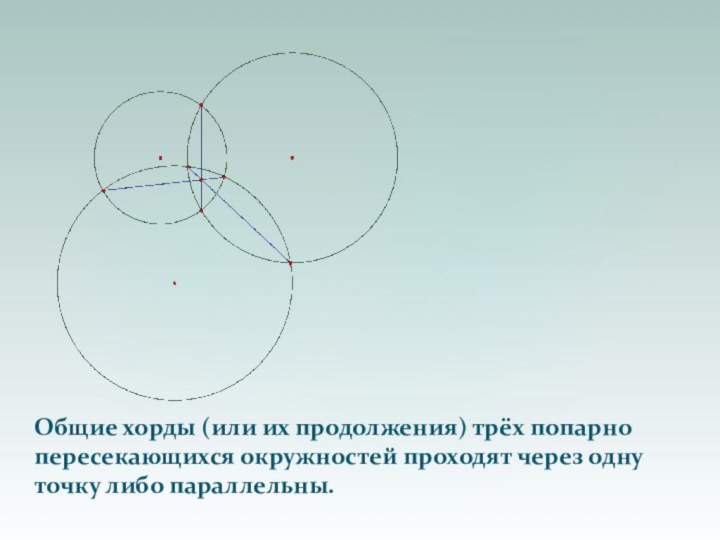
- 41. Общие хорды (или их продолжения) трёх попарно пересекающихся окружностей проходят через одну точку либо параллельны.
- 42. Две окружности касаются внутренним образом в точке
- 43. Как это работает…Если точки C и D
- 44. Если из точек C и D отрезок
- 45. Как это работает, смотрим в следующих задачах:
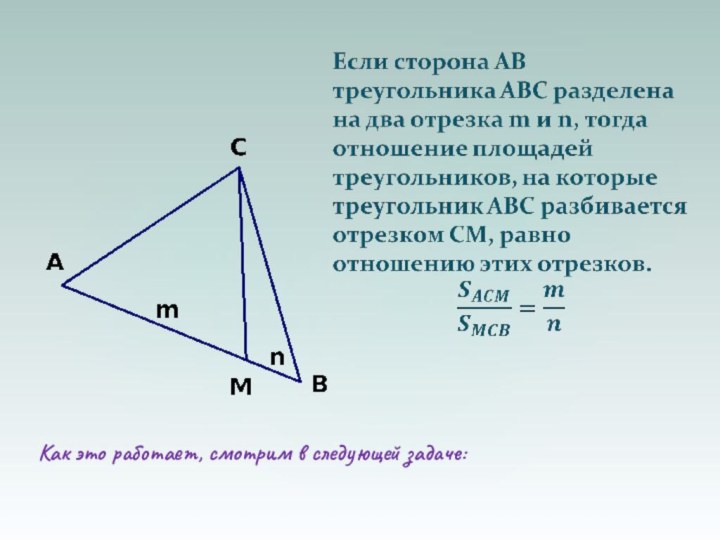
- 46. Как это работает, смотрим в следующей задаче:
- 47. Как это работает, смотрим в следующей задаче:
- 48. Как это работает…Медианы треугольника пересекаются в одной
- 49. Как это работает…
- 50. Если H точка пересечения высот треугольника ABC,
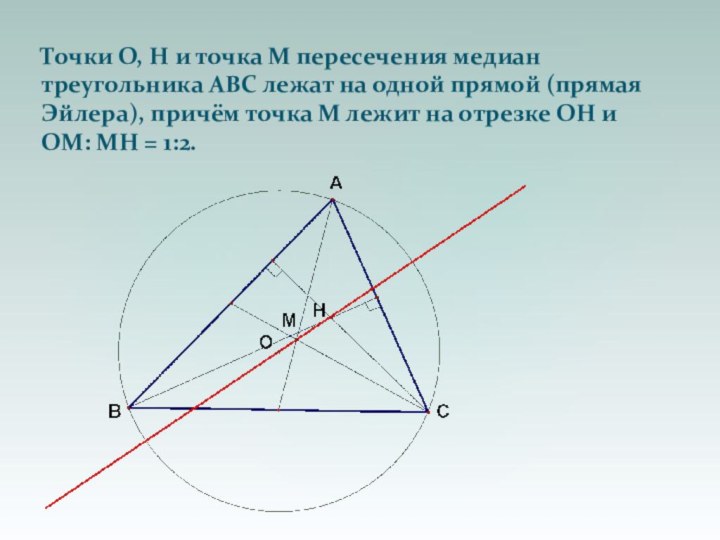
- 51. Точки О, H и точка М пересечения
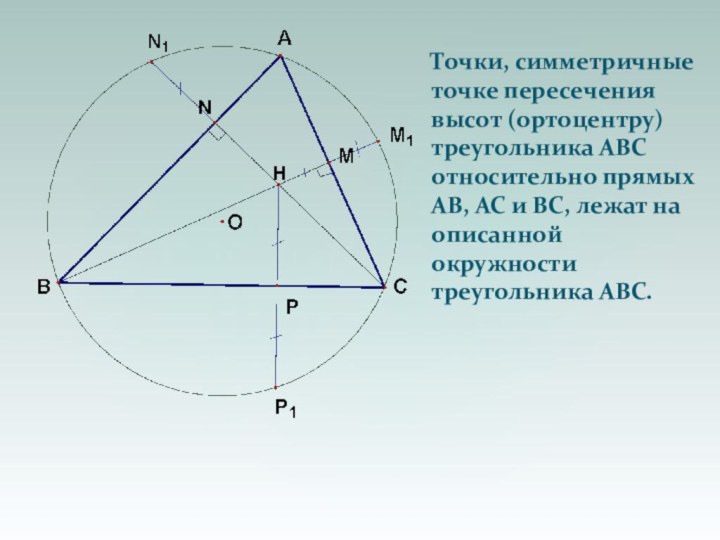
- 53. Точки, симметричные точке пересечения высот (ортоцентру) треугольника
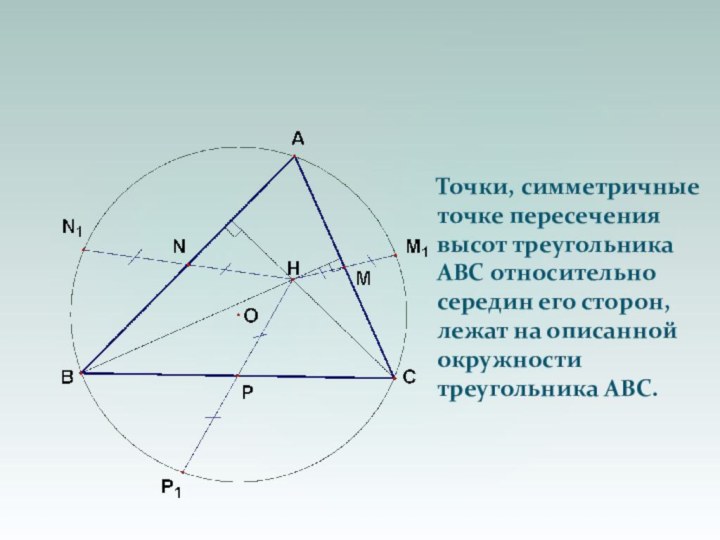
- 54. Точки, симметричные точке пересечения высот треугольника ABC
- 55. Если АК, ВМ и CN — высоты
- 56. Скачать презентацию
- 57. Похожие презентации
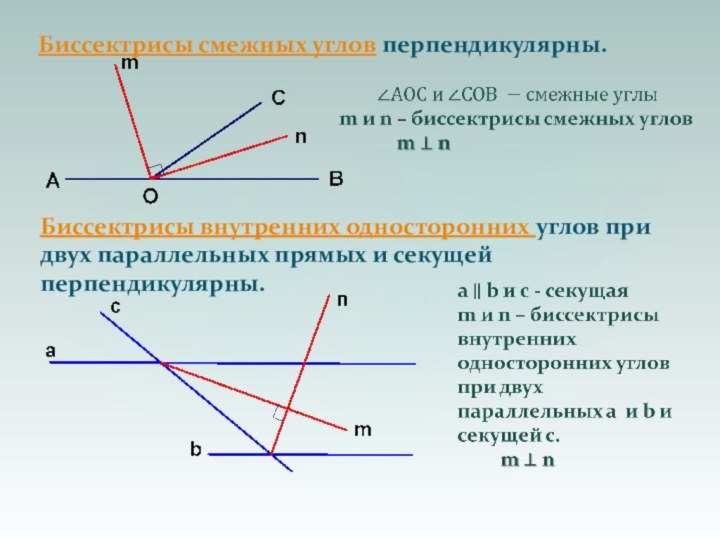
Биссектрисы смежных углов перпендикулярны. Биссектрисы внутренних односторонних углов при двух параллельных прямых и секущей перпендикулярны.


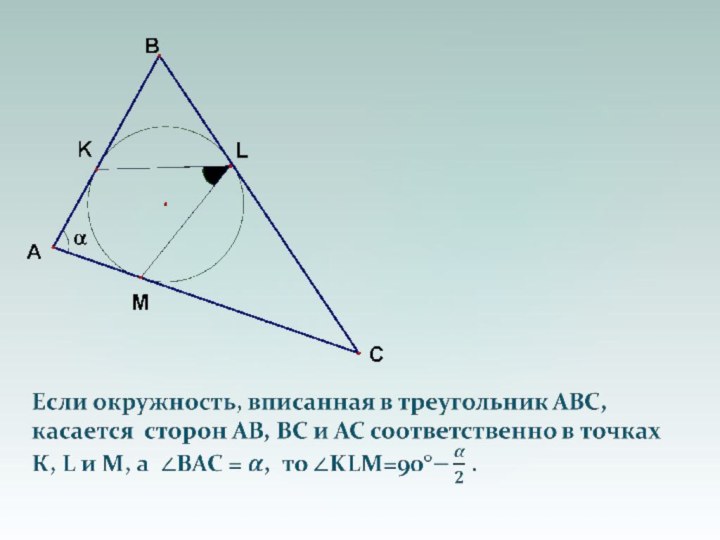























Слайд 2
Биссектрисы смежных углов перпендикулярны.
Биссектрисы внутренних односторонних углов
при двух параллельных прямых и секущей перпендикулярны.
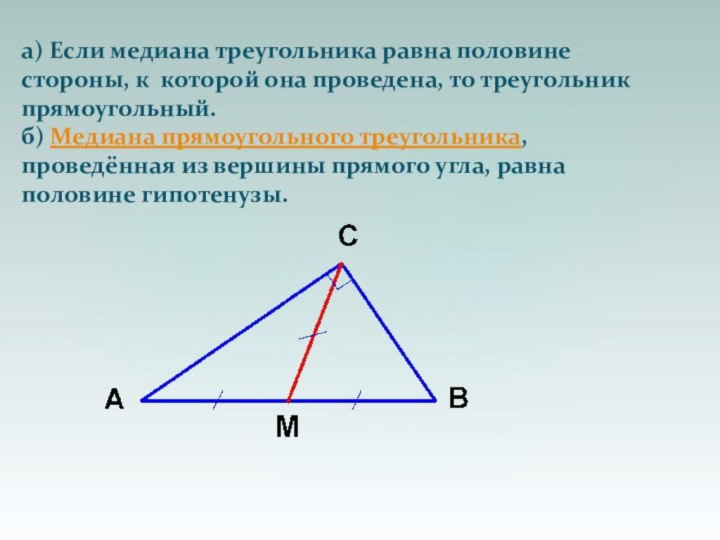
Слайд 3 а) Если медиана треугольника равна половине стороны, к
которой она проведена, то треугольник прямоугольный.
б) Медиана прямоугольного
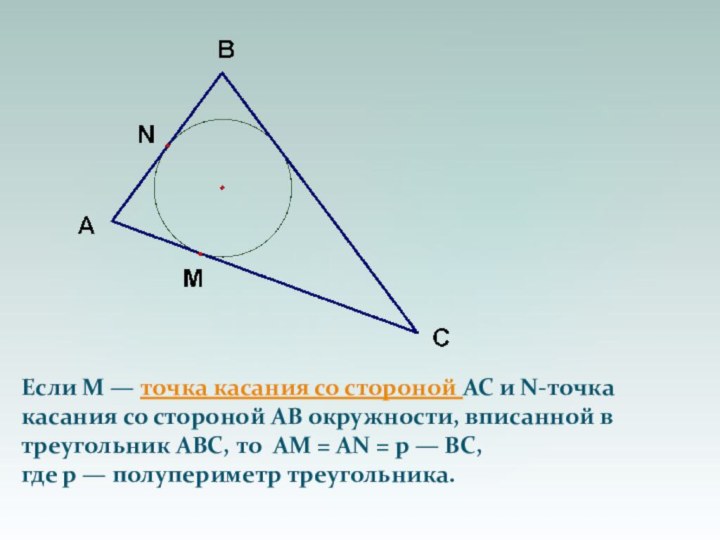
треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Слайд 5 Если М — точка касания со стороной АС
и N-точка касания со стороной АВ окружности, вписанной в
треугольник ABC, то AM = AN = р — ВС,где р — полупериметр треугольника.
Слайд 6 Если окружность касается основания ВС треугольника ABC и
продолжений сторон АВ и АС, то расстояние от вершины
А до точки касания окружности с прямой АВ равно полупериметру треугольника ABC.
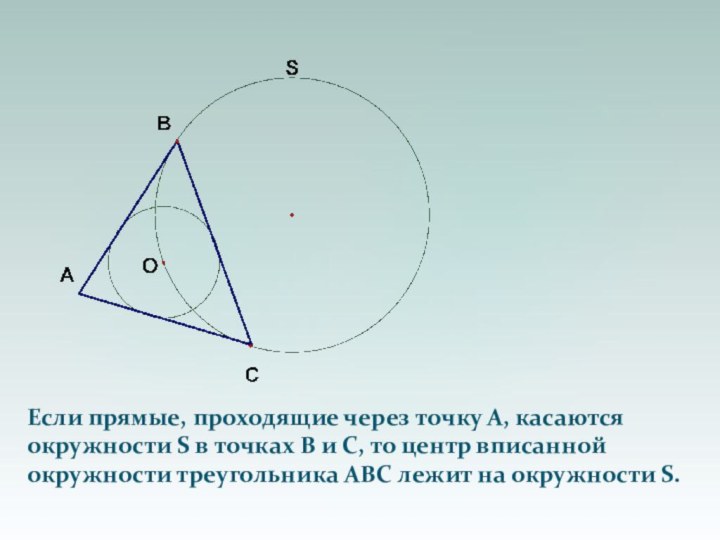
Слайд 8
Если прямые, проходящие через точку А, касаются
окружности
S в точках В и С, то центр вписанной
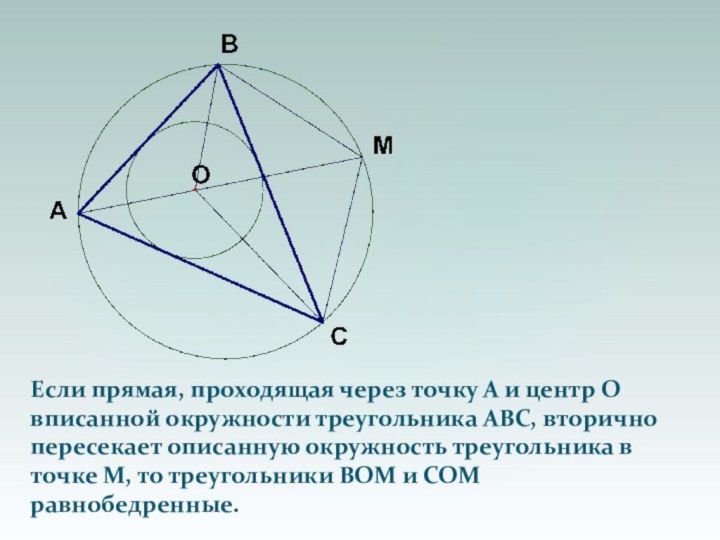
окружности треугольника ABC лежит на окружности S.Слайд 9 Если прямая, проходящая через точку А и центр
О
вписанной окружности треугольника ABC, вторично пересекает описанную окружность
треугольника в точке М, то треугольники ВОМ и СОМ равнобедренные. Слайд 15 Если сумма углов при одном из оснований трапеции
равна 90°, то отрезок, соединяющий середины оснований трапеции, равен
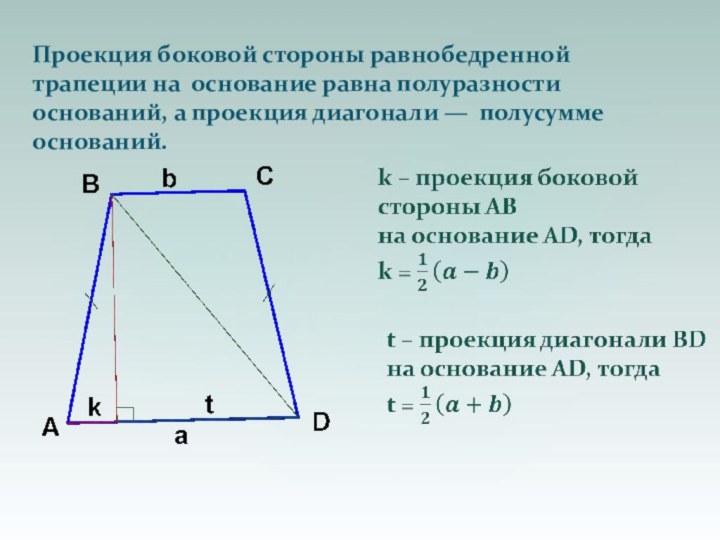
их полуразности.Слайд 16 Проекция боковой стороны равнобедренной трапеции на основание равна
полуразности оснований, а проекция диагонали — полусумме оснований.
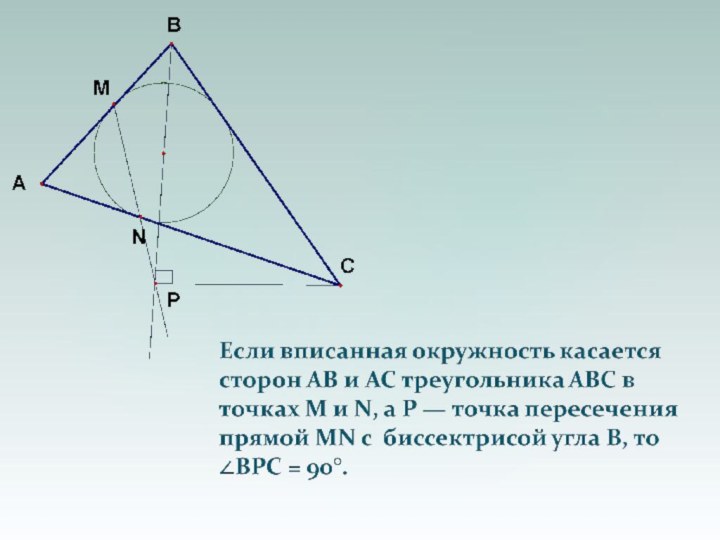
Слайд 17 Если в трапецию можно вписать окружность, то боковая
сторона трапеции видна из центра окружности под прямым углом.
Слайд 19
Если окружность вписана в равнобедренную трапецию, то
боковая
сторона трапеции равна её средней линии.
Слайд 20
Замечательное свойство трапеции.
а) Точка пересечения диагоналей трапеции,
точка пересечения продолжений боковых сторон
и середины оснований лежат
на одной прямой.
Слайд 21
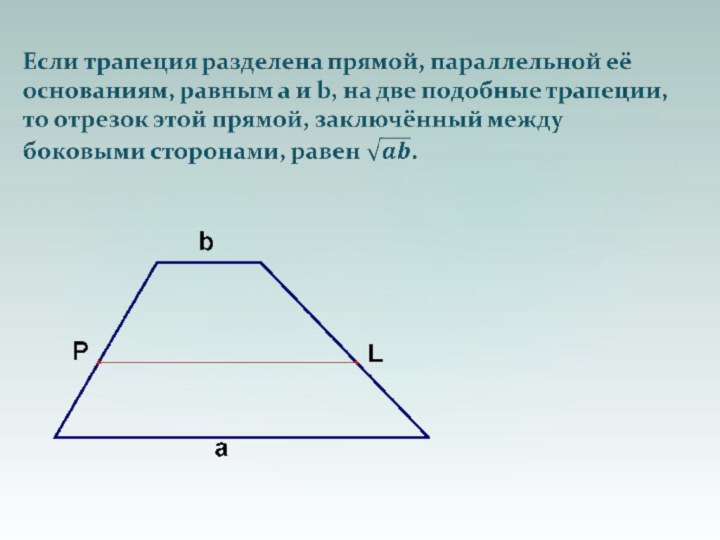
Отрезок прямой, параллельной основаниям трапеции,
заключённый внутри трапеции,
разбивается её диагоналями на три части. Тогда отрезки, прилегающие
к боковым сторонам, равны.
Слайд 24
Площадь четырёхугольника с перпендикулярными
диагоналями равна половине произведения
диагоналей.
Слайд 25 Площадь любого четырёхугольника равна половине произведения диагоналей на
синус угла между ними.
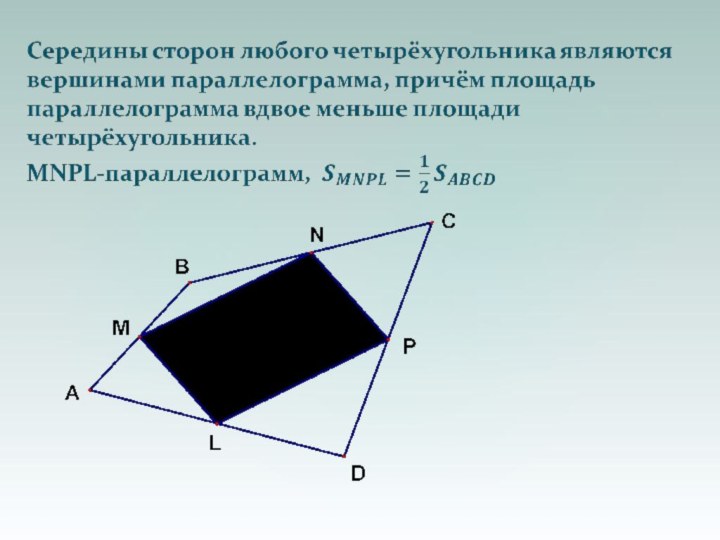
Слайд 27
Середины двух противоположных сторон любого
четырёхугольника и середины
его диагоналей либо являются вершинами параллелограмма, либо лежат на
одной прямой.
Слайд 30
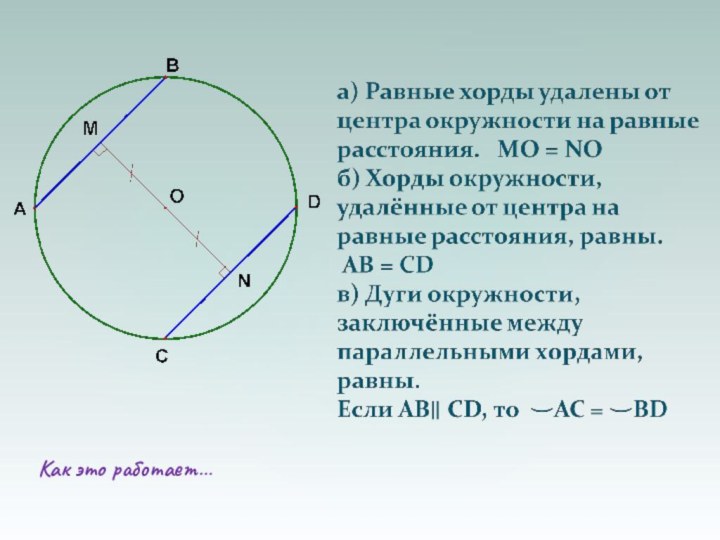
а) Диаметр, перпендикулярный хорде, делит её пополам.
б)
Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен
этой хорде.в) Серединный перпендикуляр к хорде проходит через центр
окружности.
АВ-диаметр окружности, CD-хорда, М-середина хорды CD
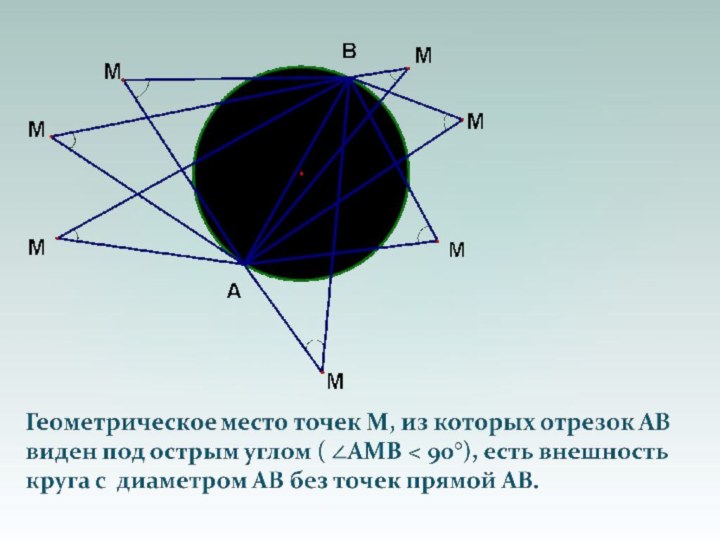
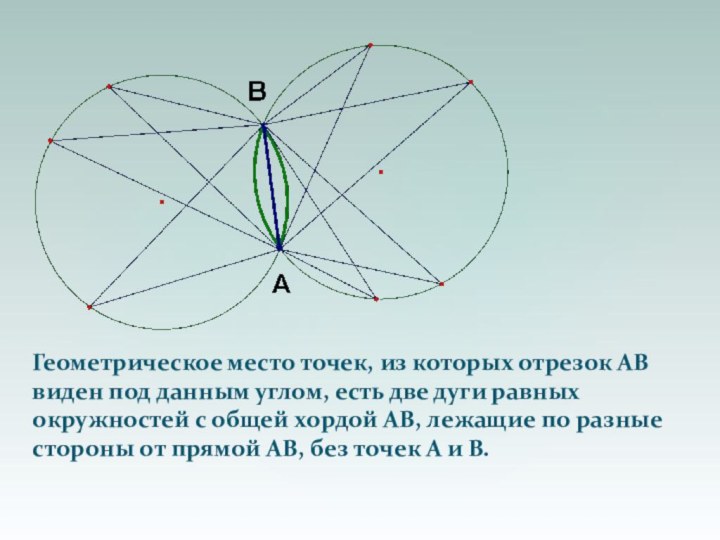
Слайд 35 Геометрическое место точек, из которых отрезок АВ виден
под данным углом, есть две дуги равных окружностей с
общей хордой АВ, лежащие по разные стороны от прямой АВ, без точек А и В.
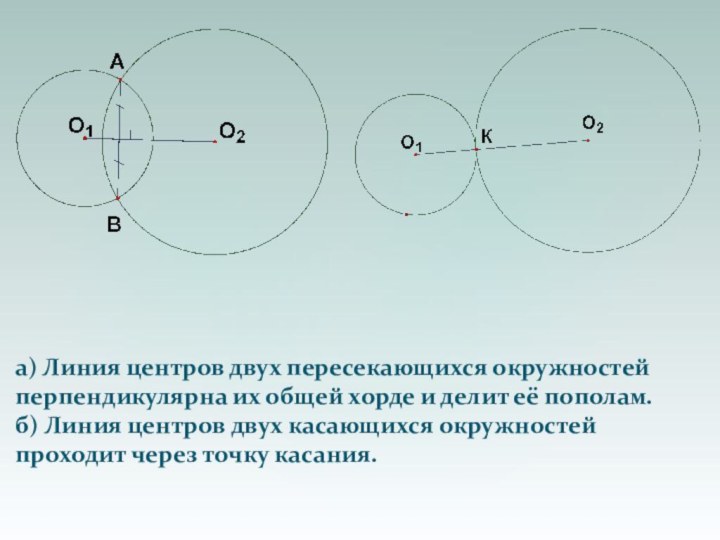
Слайд 36
а) Линия центров двух пересекающихся окружностей
перпендикулярна их
общей хорде и делит её пополам.
б) Линия центров
двух касающихся окружностей проходит через точку касания.
Слайд 40
Прямая, проходящая через точки пересечения двух
окружностей, делит
пополам общую касательную к ним.
Слайд 41
Общие хорды (или их продолжения) трёх попарно
пересекающихся
окружностей проходят через одну точку либо параллельны.
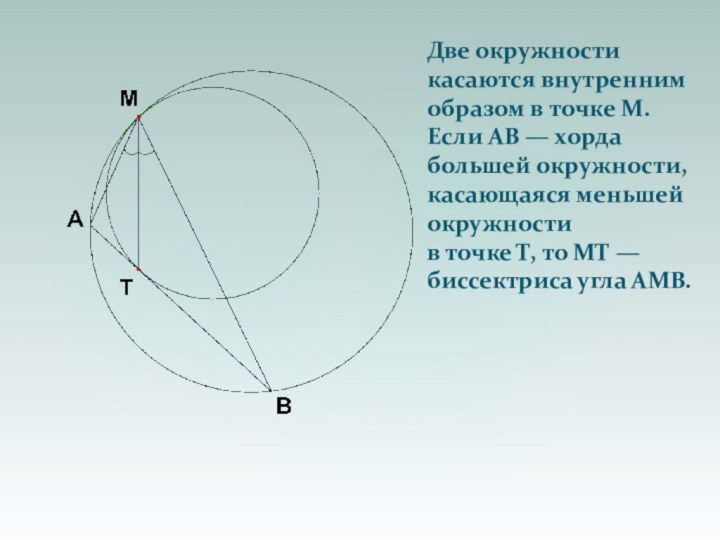
Слайд 42 Две окружности касаются внутренним образом в точке М.
Если АВ — хорда большей окружности, касающаяся меньшей окружности
в точке Т, то МТ — биссектриса угла АМВ.
Слайд 43
Как это работает…
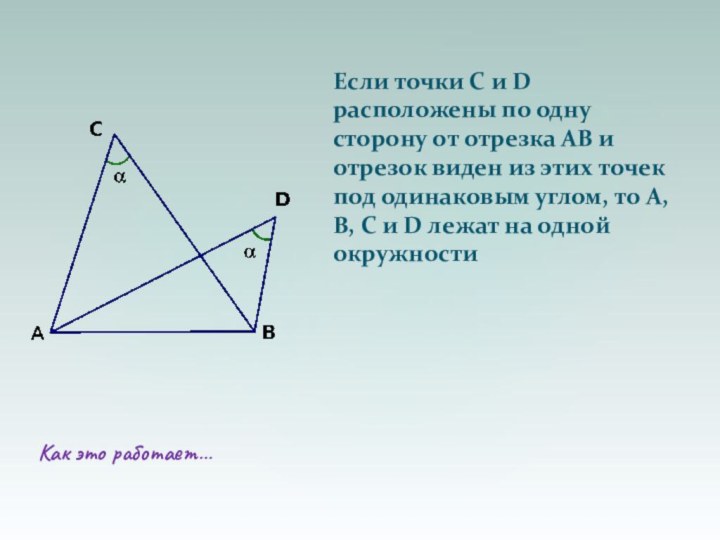
Если точки C и D расположены
по одну сторону от отрезка АВ и отрезок виден
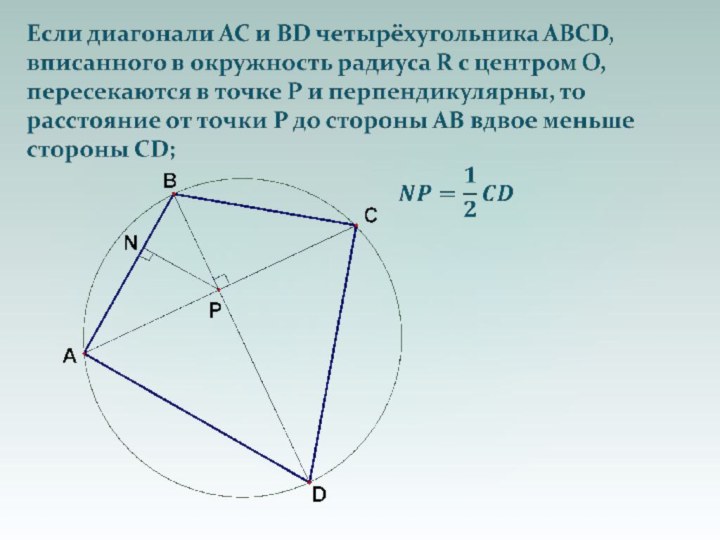
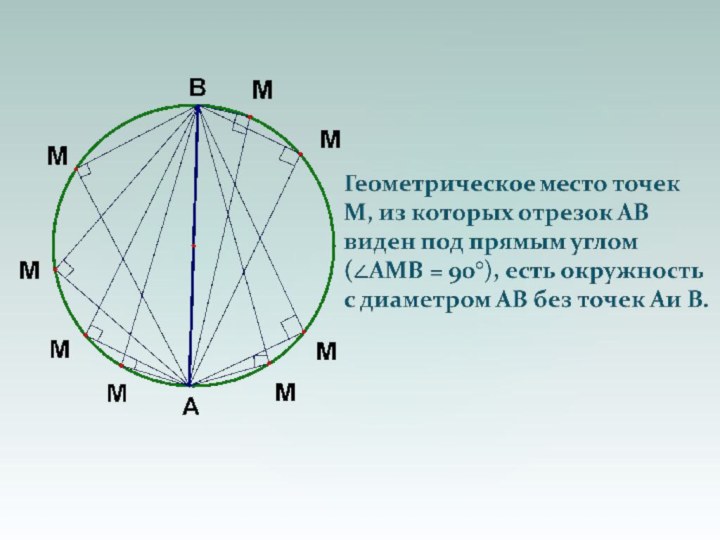
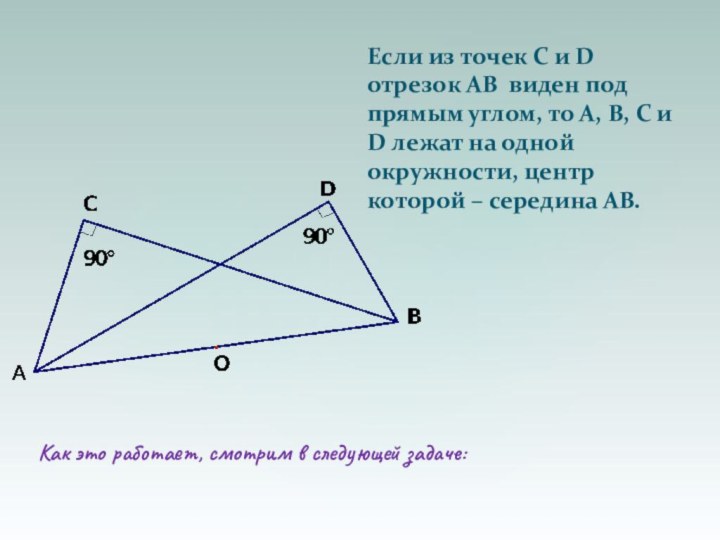
из этих точек под одинаковым углом, то А, В, С и D лежат на одной окружностиСлайд 44 Если из точек C и D отрезок АВ
виден под прямым углом, то А, В, С и
D лежат на одной окружности, центр которой – середина АВ.Как это работает, смотрим в следующей задаче:
Слайд 48
Как это работает…
Медианы треугольника пересекаются в одной точке
и делятся в ней в отношении 2 : 1,
считая от вершины.
Слайд 50
Если H точка пересечения высот треугольника ABC,
а
О — центр его описанной окружности, то отрезок АН
вдвое больше расстояния от точки О до середины стороны ВС.Как это доказать…