- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Массовая доля вещества в растворе
Содержание
- 2. Цель: закрепление понятий о растворах
- 3. Повторение темы: « Растворы»1. Что такое растворы ?
- 4. Тренировочные задания1. Кристаллические вещества, содержащие молекулы воды,
- 5. W=
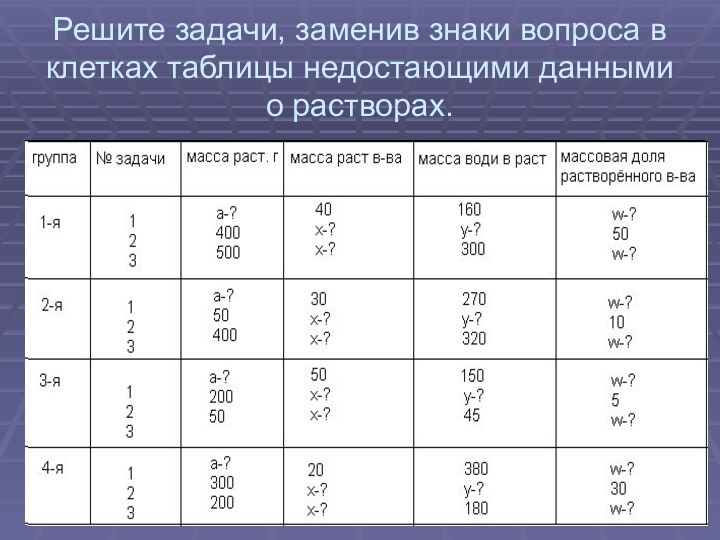
- 6. Решите задачи, заменив знаки вопроса в клетках таблицы недостающими данными о растворах.
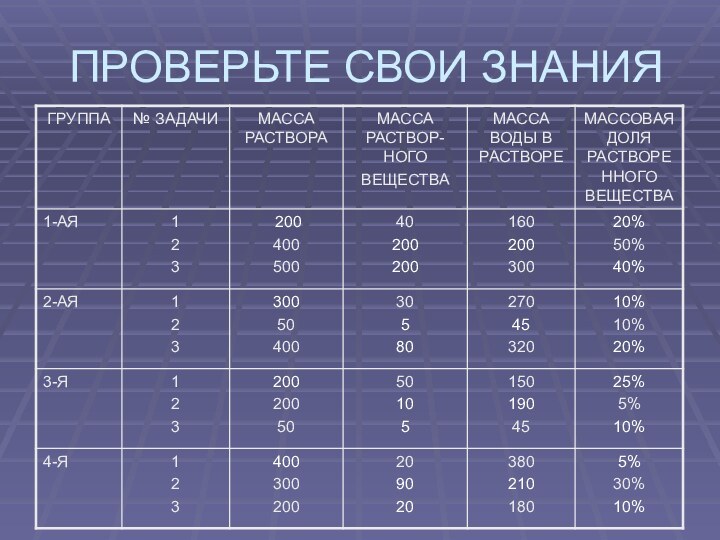
- 7. ПРОВЕРЬТЕ СВОИ ЗНАНИЯ
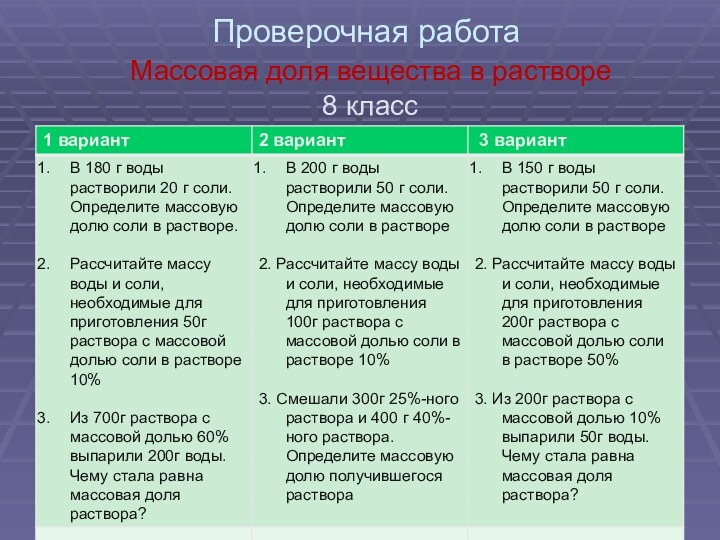
- 8. Проверочная работа Массовая доля вещества в растворе 8 класс
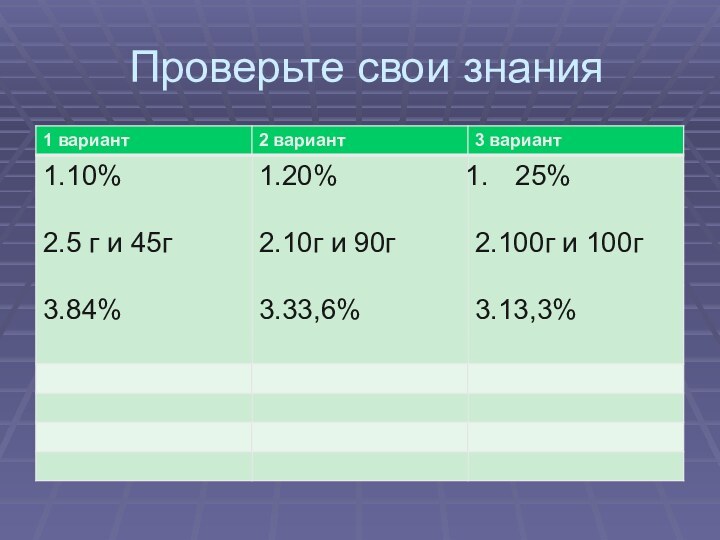
- 9. Проверьте свои знания
- 10. Диагональная модель «конверт Пирсона» или правило крестаm1•w1
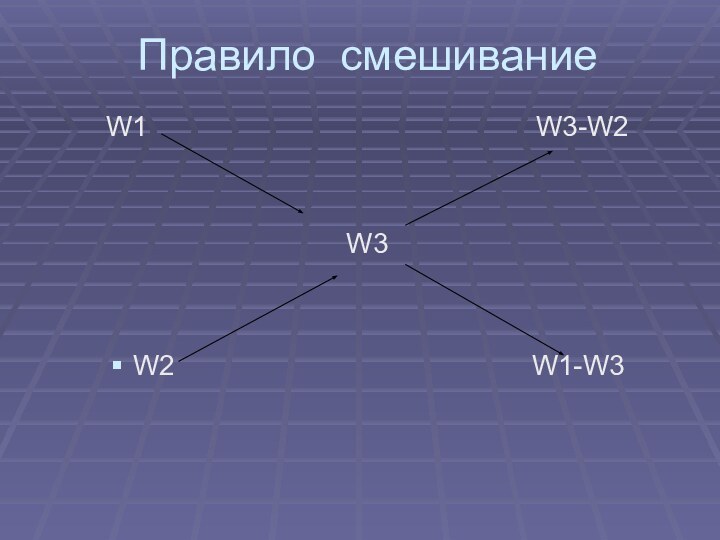
- 11. Правило смешиваниеW1
- 12. Задача: Определите концентрацию раствора, полученного при сливание
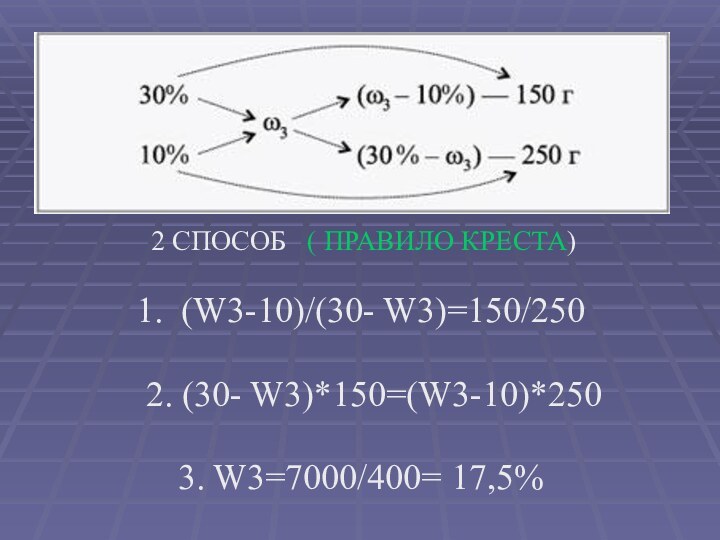
- 13. 2 СПОСОБ ( ПРАВИЛО КРЕСТА)1. (W3-10)/(30- W3)=150/250 2. (30- W3)*150=(W3-10)*2503. W3=7000/400= 17,5%
- 14. 3 способ (метод чашечек)0.3150гХ400г0,1250г150 * 0,3
- 15. СИСТЕМАТИЗАЦИЯ ЗНАНИЙ ПО ТЕМЕ: « Массовая
- 16. ПОДВЕДЕНИЕ ИТОГОВ УРОКА 1. Сформулируйте
- 17. Скачать презентацию
- 18. Похожие презентации
Цель: закрепление понятий о растворах и совершенствование знаний производить вычисления массовой доли раствора разными способами Задачи: - сформировать понятие о растворах -научиться объяснять расчетную формулу для определения массовой доли растворенного вещества с произведением










Слайд 3
Повторение темы: « Растворы»
1. Что такое растворы ?
2. Из
каких компонентов состоит жидкий раствор ?
3. Раствор отличается от смеси:
а) цветом;
б) постоянством состава;
в) оптической однородностью;
г) агрегатным состоянием.4. Что показывает коэффициент растворимости?
5. От каких факторов зависит растворимость веществ?
6. Как называется процесс образования гидратов?
Слайд 4
Тренировочные задания
1. Кристаллические вещества, содержащие молекулы воды, называют:
а)
кристаллогидратами;
б) гидратами;
в) гидридами;
г) сольватами.
2. Какие из следующих веществ являются
кристаллогидратами?а) МgSiO3; б) Sr(NО3)2•4Н2O; в) Na2СО3; г) NiCl2•Н2О.
3. По какой формуле можно рассчитать массовую долю растворенного вещества?
а) m = V•p;
б) c = n/V;
в) m(в-ва) = m(р-ра) – m(H2O);
г) w = m(в-ва)/m(р-ра).
4. Массовую долю растворенного вещества называют:
а) молярной
б) эквивалентной
в) процентной
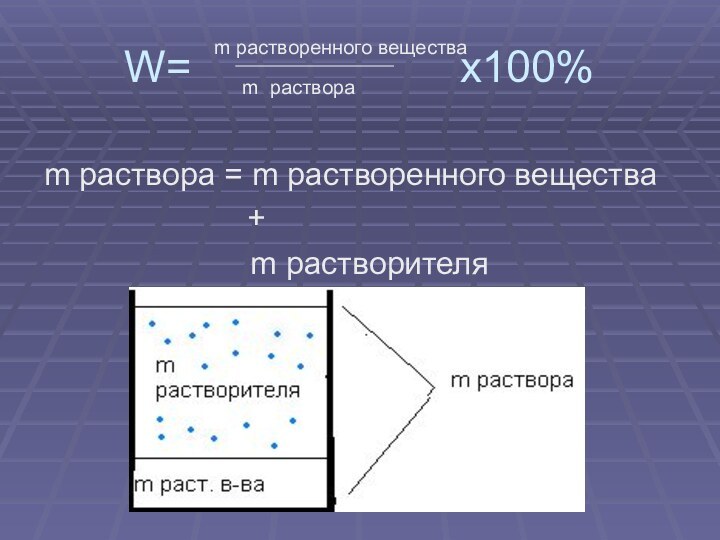
Слайд 5 W=
х100%
m раствора = m растворенного вещества
+
m растворителя
m растворенного вещества
m раствора
Слайд 10
Диагональная модель
«конверт Пирсона» или правило креста
m1•w1 + m2•w2
= w3(m1 + m2).
Отсюда
m1(w1 – w3) = m2(w3 –w
2),m1/m2 = (w3 – w2)/(w1 –w3).
Видно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворенного вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.
Слайд 12
Задача:
Определите концентрацию раствора, полученного при сливание 150г.
30%-ного и 250г. 10%-ного раствора соли
1 способ ( метод
пропорции)а) m общего раствора=150+250=400г
б) m вещества 1 =150*30/100%=45г.
в) m вещества 2 =250*10/100%=25г.
г) m общего вещества=45+25=70г.
д) W в-ва в полученном растворе=70*100%/400=17,5%
Слайд 13
2 СПОСОБ ( ПРАВИЛО КРЕСТА)
1. (W3-10)/(30-
W3)=150/250
2. (30- W3)*150=(W3-10)*250
3. W3=7000/400= 17,5%
Слайд 14
3 способ (метод чашечек)
0.3
150г
Х
400г
0,1
250г
150 * 0,3 +
250 * 0,1 = 400 * Х
45+25 = 400
* ХХ = 0,175 или 17,5%