- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике Элементы комбинаторики (5-6 класс)
Содержание
- 2. Комбинаторика – это раздел математики, посвящённый задачам
- 3. Примеры комбинаторных задачПримерНесколько стран в качестве символа
- 4. Ответ . 6 комбинацийФлаг
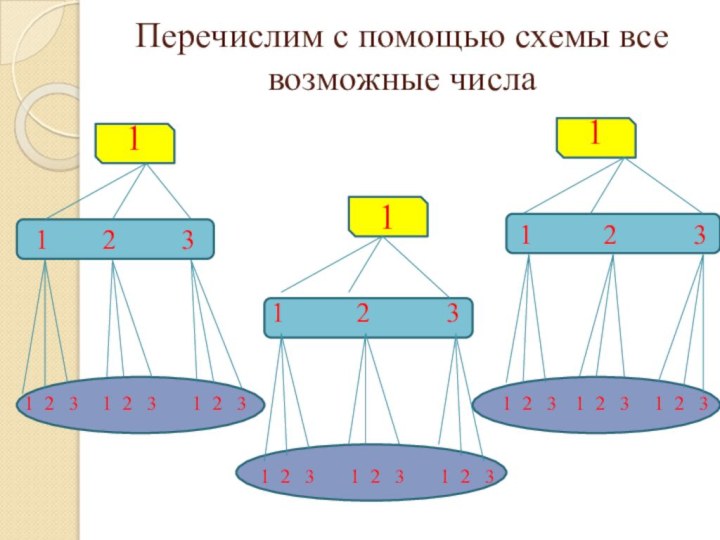
- 5. Сколько трехзначных чисел можно составить из 3 цифр: 1, 2, 3?Пример
- 6. Перечислим с помощью схемы все возможные числа1321
- 7. Сколько трехэлементных подмножеств, различающихся хотя бы одним
- 8. Перечислим все полученные подмножества:(1, 2, 3), (1,
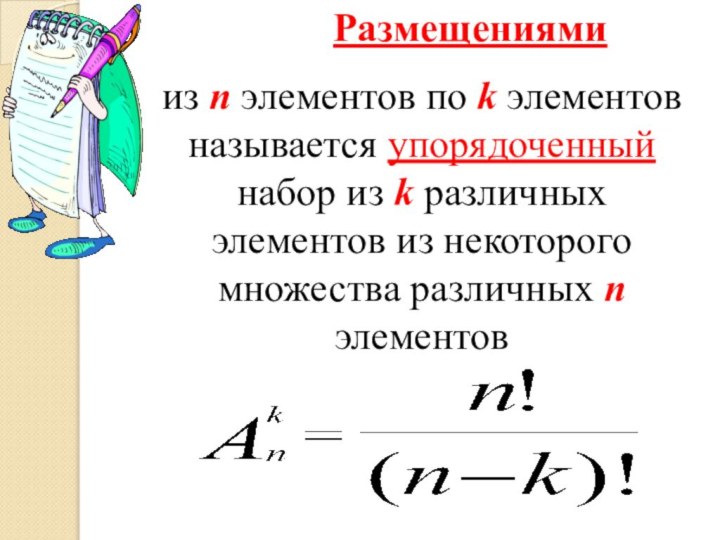
- 9. Размещениямииз n элементов по k элементов называется
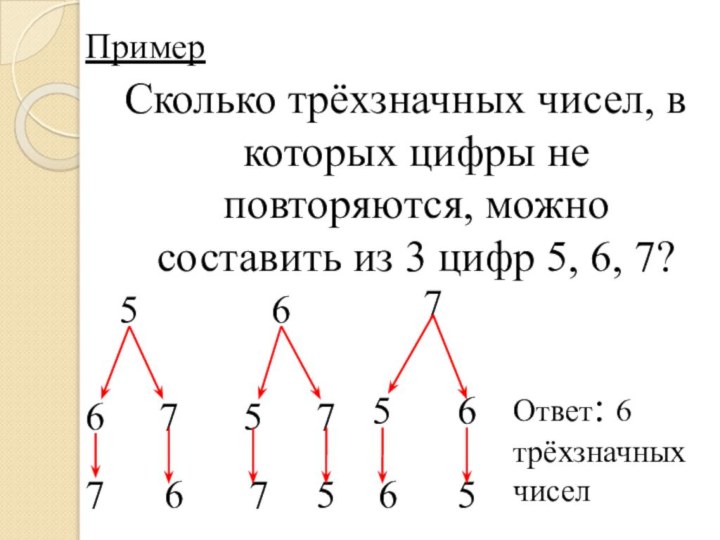
- 10. ПримерСколько трёхзначных чисел, в которых цифры не
- 11. ПримерИз команды в 10 человек нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
- 12. ПримерАнтон, Борис и Василий купили три билета
- 13. АААВБББВМожет быть такая последовательность:А может быть и так:ВВАБМожет быть и так:ВВААББОтвет: 6 вариантовЗаметим, что 3!=6
- 14. ПримерСколько существует двузначных чисел, в которых цифра десятков и цифра единиц различны и нечетны?
- 15. Размещениями с повторениями из n элементов по k называются упорядоченные k-элементные выборки, в которых элементы могут повторяться.
- 16. ПримерВозьмем буквы Б, А, Р. Какие размещения из
- 17. ЗапомнитеРазмещением называется расположение “предметов” на некоторых “местах”
- 18. Перестановки -это множество из n различных элементов, записанных в определённом порядке
- 19. Формула перестановок с повторениями Отображение множества k первых
- 20. ПримерСколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?
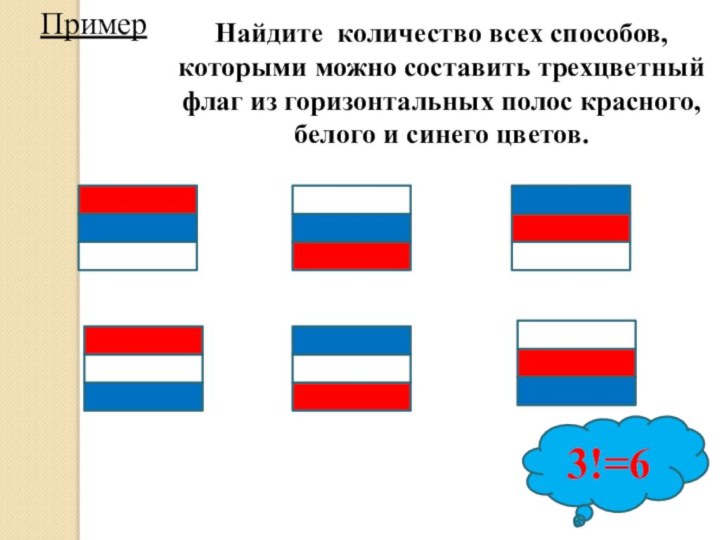
- 21. Найдите количество всех способов, которыми можно составить
- 22. Сочетаниямииз n элементов по k в
- 23. ПримерНа 5 сотрудников выделено 3 путевки в
- 24. Сочетанием с повторениями из n элементов по k называется неупорядоченный набор, содержащий k элементов, каждый из которых может быть одного из n типов
- 25. ПримерСколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4?
- 26. Если при выборе не важен порядок расстановки между ними, то такие комбинации называются сочетаниямиЗапомните
- 27. Простейшие комбинации
- 28. Скачать презентацию
- 29. Похожие презентации
Комбинаторика – это раздел математики, посвящённый задачам выбора и расположения предметов из раздела множеств. Типичной задачей комбинаторики является задача перечисления комбинаций, составленных из нескольких предметов.























Слайд 3
Примеры
комбинаторных задач
Пример
Несколько стран в качестве символа своего госу-
дарства решили использовать флаг в виде 3-х гори-зонтальных полос
одинаковых по ширине и цвету: синий, красный и белый.Сколько стран могут испытать такую символику при условии, что у каждой страны свой отличный от других флаг?
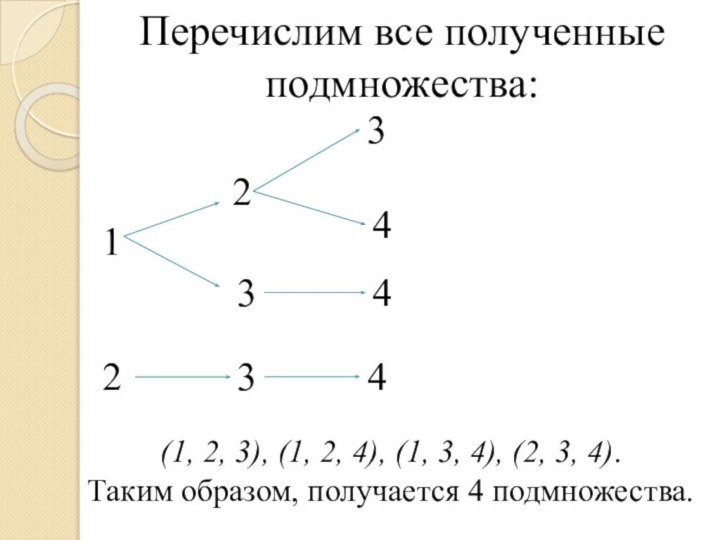
Слайд 7 Сколько трехэлементных подмножеств, различающихся хотя бы одним элементом
друг от друга и без учета порядка в подмножестве,
можно составить из 4 цифр: 1, 2, 3, 4?Пример
Слайд 8
Перечислим все полученные подмножества:
(1, 2, 3), (1, 2,
4), (1, 3, 4), (2, 3, 4).
Таким образом, получается
4 подмножества.1
2
2
3
3
3
4
4
4
Слайд 9
Размещениями
из n элементов по k элементов называется упорядоченный
набор из k различных элементов из некоторого множества различных
n элементов
Слайд 10
Пример
Сколько трёхзначных чисел, в которых цифры не повторяются,
можно составить из 3 цифр 5, 6, 7?
Ответ: 6
трёхзначных чисел
Слайд 11
Пример
Из команды в 10 человек нужно выбрать капитана
и его заместителя. Сколькими способами это можно сделать?
Слайд 12
Пример
Антон, Борис и Василий купили три билета на
1-е, 2-е и 3-е места первого ряда на футбольный
матч. Сколькими способами они могут занять имеющиеся места?
Слайд 13
А
А
А
В
Б
Б
Б
В
Может быть такая последовательность:
А может быть и так:
В
В
А
Б
Может
быть и так:
В
В
А
А
Б
Б
Ответ: 6 вариантов
Заметим, что 3!=6
Слайд 14
Пример
Сколько существует двузначных чисел, в которых цифра десятков
и цифра единиц различны и нечетны?
Слайд 15 Размещениями с повторениями из n элементов по k называются упорядоченные k-элементные выборки, в которых
элементы могут повторяться.
Слайд 16
Пример
Возьмем буквы Б, А, Р. Какие размещения из этих
букв, взятых по две, можно получить? Сколько таких наборов
получиться, если буквы могут повторяться?Получаем наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА
Слайд 17
Запомните
Размещением называется расположение “предметов” на некоторых “местах” при
условии, что каждое место занято в точности одним предметом
и все предметы различны.В размещении учитывается порядок следования предметов. Так, например, наборы (2,1,3) и (3,2,1) являются различными
Слайд 19 Формула перестановок с повторениями Отображение множества k первых натуральных чисел 1,
2,…, k в данное множество
, называется перестановкой с повторениями, составленным из данных n элементов по k гдеСлайд 21 Найдите количество всех способов, которыми можно составить трехцветный
флаг из горизонтальных полос красного, белого и синего цветов.
3!=6
Пример