Слайд 2
Цели урока:
: Развивающие: создать условия для развития познавательной
активности учащихся, познавательного интереса к предмету; развивать навыки самостоятельной
деятельности учащихся; развивать навыки самоконтроля; развивать активность учащихся, формировать учебно-познавательные действия, коммуникативные, исследовательские навыки учащихся, умение анализировать и устанавливать связь между элементами темы.
Воспитывающие: создать условия успешности ученика на уроке; воспитывать культуру умственного труда; способность к самоанализу, рефлексии; развивать умение рецензировать и корректировать ответы товарищей. воспитывать умение критически относиться к результатам деятельности; обеспечить гуманистический характер Цели обучения;
Слайд 3
Взаимное расположение двух прямых на плоскости :
Определение:
Прямые, которые не пересекаются и не лежат в одной
плоскости, называются скрещивающимися
Определение.Если прямые имеют одну общую точку и лежат в одной плоскостей, то они пересекаются.
Определение:Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекются
Слайд 4
Параллельные прямые в пространстве
Задача (3). Докажите, что все
прямые, пересекающие две данные параллельные прямые, лежат в одной
плоскости.
Решение. Так как данные прямые ɑ и Ь параллельны, то через них можно провести плоскость (рис. 323). Обозначим ее . Прямая с, пересекающая данные параллельные прямые, имеет с плоскостью две общие точки — точки пересечения с данными прямыми. По теореме 15.2 эта прямая лежит в плоскости . Итак, все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости — плоскости .
Слайд 5
Параллельные прямые в пространстве
16.1. Через точку вне данной
прямой можно провести прямую, параллельную этой прямой, и притом
только одну.
Замечание. Утверждение единственности в теореме 16.1 не является простым следствием аксиомы параллельных, так как этой аксиомой утверждается единственность прямой, параллельной данной в данной плоскости. Поэтому она требует доказательства.
Доказательство. Пусть ɑ — данная прямая и А — точка, не лежащая на этой прямой (рис. 324). Проведем через прямую ɑ и точку А плоскость . Проведем через точку А в плоскости прямую ɑ1, параллельную ɑ. Докажем, что прямая ɑ1, параллельная ɑ, единственна.
Допустим, что существует другая прямая ɑ?, проходящая через Рис. 324 точку А и параллельная прямой ɑ.
Через прямые ɑ и ɑ2можно провести плоскость ɑ2- Плоскость проходит через прямую ɑ и точку А-, следовательно, по теореме 15.1 она совпадает с ɑ. Теперь по аксиоме параллельных прямые ɑ1 и ɑ2совпадают. Теорема доказана.
Слайд 6
Признак параллельность прямых
Теорема 16.2. Две прямые, параллельные третьей

прямой, параллельны.
Доказательство. Пусть прямые Ь и с параллельны прямой
ɑ. Докажем, что прямые Ь и с параллельны.Случай, когда прямые ɑ, Ь, с лежат в одной плоскости, был рассмотрен в планиметрии. Поэтому предположим, что наши прямые не лежат в одной плоскости. Пусть — плоскость, в которой лежат прямые ɑ и Ь, а у — плоскость, в которой лежат прямые ɑ и с. Плоскости и различны. Отметим на прямой Ь какую-нибудь точку В и проведем плоскость через прямую с и точку В. Она пересечет плоскость по прямой Ь1.Прямая b1 не пересекает плоскость. Действительно, точка пересечения должна принадлежать прямой ɑ, так как прямая Ь1 лежит в плоскости С другой стороны, она должна лежать и на прямой с, так как прямая b1 лежит в плоскости -Но прямые ɑ и с как параллельные не пересекаются.Так как прямая Ь1 лежит в плоскости и не пересекает прямую ɑ, то она параллельна ɑ, а значит, совпадает с b по аксиоме параллельных. Таким образом, прямая Ь, совпадая с прямой Ь1, лежит в одной плоскости с прямой с (в плоскости) и не пересекает ее. Значит, прямые Ь и с параллельны. Теорема доказана.
Слайд 7
Признак параллельности прямой и плоскости
Задача (11). Докажите, что
середины сторон пространственного четырехугольника являются вершинами параллелограмма (вершины пространственного
четырехугольника не лежат в одной плоскости).
Решение. Пусть ABCD — данный пространственный четырехугольник (рис. 326). Пусть А1, В1, С1, D1 — середины его сторон. Тогда А 1 В1 — средняя линия треугольника ABC, параллельная стороне AC, C 1D1—средняя линия треугольника ACD, тоже параллельная стороне АС. По теореме 16.2 прямые
А 1В 1 и C 1D 1, параллельны, а значит, лежат в одной плоскости. Точно так же доказывается параллельность прямых A 1D1 и В 1С 1. Итак, четырехугольник
А 1В 1 C 1D 1 лежит в одной плоскости и его противолежащие стороны параллельны. Следовательно, он параллелограмм.
138. Признак параллельности прямой плоскости
Прямая и плоскость называются параллельными, если они не пересекаются
Слайд 8
Параллельность прямой и плоскости.
Теорема 16.3. Если прямая, не
принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то
она параллельна и самой плоскости.
Доказательство. Пусть α — плоскость, ɑ — не лежащая в ней прямая и ɑ 1 — прямая в плоскости α, параллельная прямой ɑ. Проведем плоскость α1 через прямые ɑ и ɑ1
Плоскости α и α1 пересекаются по прямой ɑ 1. Если бы прямая ɑ пересекала плоскость α, то точка пересечения принадлежала бы прямой ɑ1. Но это невозможно, так как прямые ɑ и ɑ1 параллельны.
Итак, прямая ɑ не пересекает плоскость α, а значит, параллельна
плоскости α. Теорема доказана.
Слайд 9
Параллельность прямой и плоскости.
Слайд 10
Признак параллельности плоскостей
Две плоскости называются
параллельными, если они не
пересекаются.
Теорема 16.4. Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Доказательство. Пусть α и β данные плоскости, ɑ2 и ɑ1 — прямые в плоскости α, пересекающиеся в точке А, Ь1 и Ь2 — соответственно параллельные им прямые в плоскости β. Допустим, что плоскости α и β не параллельны, т. е. пересекаются по некоторой прямой с. По теореме 16.3 прямые ɑ2 и ɑ1 , как параллельные прямым Ь1 и Ь2 » параллельны плоскости β, и поэтому они не пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости α через точку А проходят две прямые (ɑ2 и ɑ1), параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию. Теорема доказана.
Слайд 11
Признак параллельности плоскостей
№6
Дано куб АВСD А 1В 1С
1D1. А)Укажите параллельные ребры куба.Сколько параллельных ребер с одним
ребром ? Б) Укажите скрещиваюшиеся ребры. Сколько скрещивающихся ребер с одним ребром.
Слайд 12
Признак параллельности прямой и плоскости
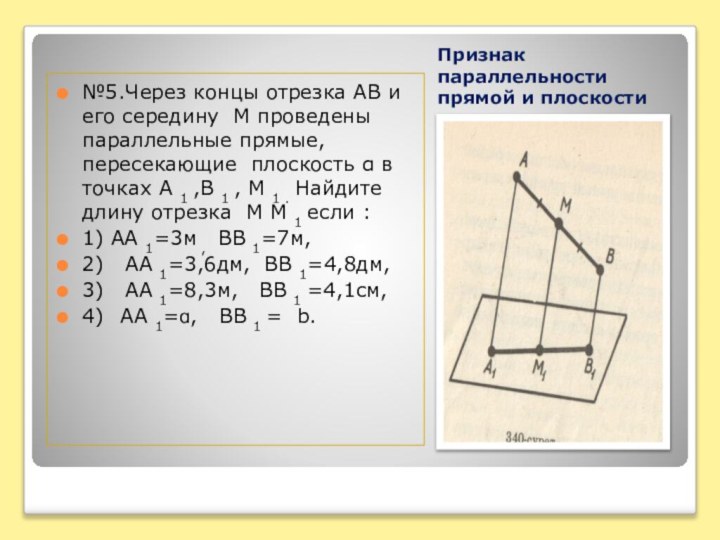
№5.Через концы отрезка АВ
и его середину М проведены параллельные прямые, пересекающие плоскость
α в точках А 1 ,В 1 , М 1 . Найдите длину отрезка М М 1 если :
1) АА 1=3м , ВВ 1=7м,
2) АА 1=3,6дм, ВВ 1=4,8дм,
3) АА 1=8,3м, ВВ 1 =4,1см,
4) АА 1=ɑ, ВВ 1 = b.
Слайд 13
Признак параллельности прямой и плоскости
№6*. Отрезок АВ пересекает
плоскость α. Через концы отрезка в его середину М
проведены параллельные прямые,пересекающие плоскость α в точках
А 1 ,В 1 , М 1 .Найдите длину отрезка
М М 1, если АА 1=5,7см ,
ВВ 1=8,5см.
Жауабы.7,1 см
Слайд 14
Признак параллельности прямой и плоскости.
№7. Через конец А
отрезка проведена плоскость. Через конец В и точку С
этого проведены параллельные прямые , пересекающие плоскость в точках В 1 и С 1 . Найдите длину отрезка ВВ1 :
1) СС 1=15м , АС:ВС=2:3;2) СС1=8,1см, АВ:АС=11:9 ;3) АВ= 6 см, АС: СС1 =2:5 ;
4) АС =ɑ, ВС = b, СС 1=с .
Слайд 15
№8*. Даны АВСD параллелограм и не пересекающая его
плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную
плоскость в точках А 1 ,В 1 ,С 1,D1.Найдите длину отрезка DD1, если: 1) АА 1=2м , ВВ 1=3м, СС1=8м 2) АА 1=4м , ВВ 1=3м, СС1=1м 3) АА 1=ɑ, ВВ 1 =b,СС 1 = с
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.
Слайд 16
Домашнее задание
П. 136, 137,138,139;
№7 Основание пирамиды
SABCD –квадрат. Точки K,M,N,P,R середины сторон AS, DS,AD,SB,AB
. а) KMII BC; б) PR IIMN .
Приведите примеры на параллельные прямые в пространстве.
Слайд 17
Библиография
А.В. Погорелов
«Геометрия, 7-11», М., Алматы: Рауан, 1997