и систематизировать знания, умения и навыки, необходимые для нахождения
вероятности событий при решении задач на ЕГЭРазвитие умений сравнивать, обобщать, находить различные способы решения задач.
Воспитание умение ставить цели и реализовывать их.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

























ООР
ОРО
ОРР
РОО
РОР
РРО
РРР
В группе иностранных туристов 51 человек, среди них 2 француза. Для посещения маленького музея группу случайным образом делят на 3 подгруппы, одинаковые по численности. Найдите вероятность того, что французы окажутся в одной подгруппе.
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Найдем вероятности наступления такой погоды:
P(XXO) = 0,8·0,8·0,2 = 0,128;
P(XOO) = 0,8·0,2·0,8 = 0,128;
P(OXO) = 0,2·0,2·0,2 = 0,008;
P(OOO) = 0,2·0,8·0,8 = 0,128.
Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.
происходят
оба события
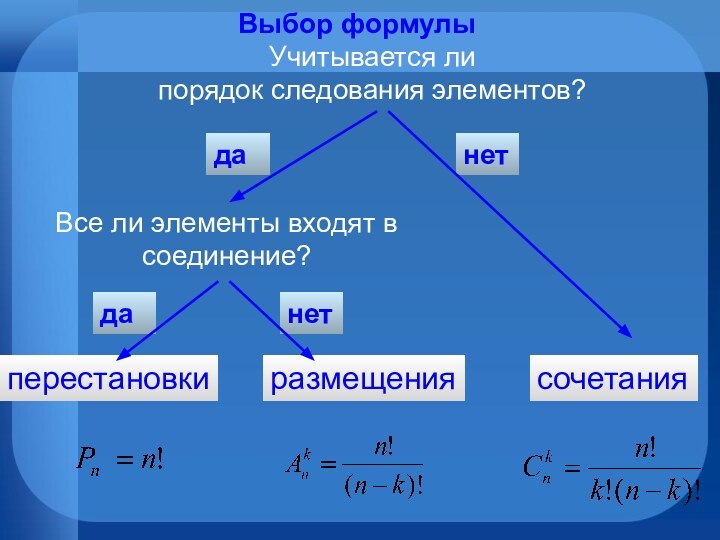
Правила комбинаторики
-
вероятность того, что второй школьник станет
обменивать ручку другого цвета
Т.к. по условию школьники
не пронумерованы,
то искомая вероятность
Вероятность того, что обе чёрные ручки окажутся у второго школьника
Из трёх монет две зафиксированы,
выбираем из 8-2=6 монет
3-2=1 монету по рублю
Возможны 2 варианта: либо Петя двухрублёвые монеты вообще не перекладывал, либо переложил сразу обе.
Если двухрублевые монеты не перекладывались, то 3 монеты по рублю можно выбрать из 4 способами.
Если обе двухрублевые монеты переложены, то еще одну рублевую монету можно выбрать из 4 способами.
Всего выбираем 3 монеты из 4+2=6 способами.
Всего Петя переложил 3 монеты, придется переложить еще 2 монеты по 10 рублей. Таких монет у Пети 4, поэтому количество способов равно
Переложить 3 монеты из 6 имеющихся можно способами.